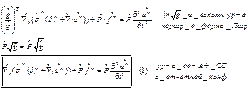Понятие силы. Классификация сил. Плотность массовых и поверхностных сил. Вектор напряжений. Напряженное состояние.
Силы делятся на массовые и поверхностные.
Массовые – те которые действуют на … тела (сила тяжести)
Поверхностные – те которые возникают в результате непосредственного соприкосновения тел.
Плотность массовых сил - сила действующая на ед. массы
Плотность поверхностных сил - сила действующая на ед. площади.
Вектор напряжений:
Силы взаимод. делятся на внутренние и внешние, они могут быть как массовыми так и поверхностными.
Вектор Pn – вектор напряжений.
Pn=-P-n
Совокупность всех векторов напряжений определяет напряженное состояние в этой точке. т.е. можно сделать сечение, ориент. другой нормалью.
Тензор напряжений Коши. Формула Коши.
| 
|
|
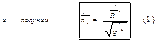
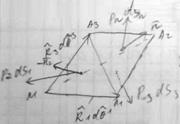
Нормали к коорд. площ. будут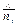 
через Pi об. векторы напряж. ориентир 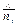тогда поверх. силы, приложенные к этому тетраэдру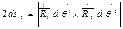 
На площади А1 А2 А3 введем нормаль и вектор напряжений. Примем, что на этот тетраэдр действуют силы f и –w, согласно принципу Даламбера главный вектор сил =0
Разделим на dSn и перейд. к пред. при усл. 
(т.к. в числ. вел. третьего пор. малости)
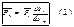Найдем 
, найдем 
(3) в (2) => 
Вектор 
тогда 
Пусть в кажд. сис. корд. заданы числа 
, из (5) свертка этих числед с произв. вект. дают нам тензор первого ранга => что парам явл. комп. тензора.
Об.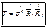 
- наз. тензором напряжения Коши
(5) перепишем: 
- ф-ла Коши
Симметричность тензора напряжений Коши
| 
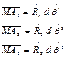Найдем центры тяж. кажд. корж. площ. MA1A2 ~ dS3 Как найти C3?
|
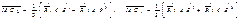получ. три центра корд. площ. постр. С- центр четвертой грани
| 
|
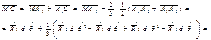
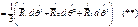
чтобы тетраидр находился в равн. главные мом =0 и гл. вект =0
приравниваем нулю главные мом относительно т. С
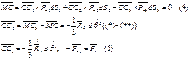
(5) в (4) =>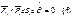 
| Рассмотрим dS3-площ. |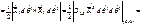 
|
Отметим, что объем парал.
Если из (7) подст в (6)и учесть (8):
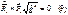из (3) => 
что и док. симметр. тенз. напр-я.
Механический смысл компонент тензора напряжений в ортогональных криволинейных коорд.
| Если есть тензор аij, то Рассм. |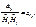 
|
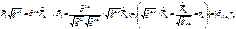
т.е.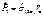 
- в ортонорм. сис. 
- явл. комп. вект. напр. 
| А – центр тяжести
P3 – вект. напр-я, в этом и есть смысл комп. тен.
Первый индекс указывает на направл. нормали, а второй на на правление действия
|
Принцип сохранения массы. Уравнение неразрывности в переменных Лагранжа
Приним, что масса любого индив. объема сплошн среды при ее движ. не изменяется.
- т.е. скор. изм. массы =0
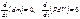
Лемма: Пусть j(m) – непр-я ф-я заданная в обл. D, mÎD, VCD - " подобласть, если для " V 
Д-во: Действ предп. что не так, m0ÎD: j(m)>0, в след того что j - непр. $ окр. Т. m0 , такая что NÎu(m0), j(N)>0. тогда получ что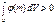 
это противоречит.
урав-я неразрывности в форме лагранжа.
Если задан. индив. объем, то массу можем выс. как в простр, так и в материальных коорд.
Выч. массу 
- масса, если выч. произв по времени масса сохран, объем меняется, т.е. завис. от времени.
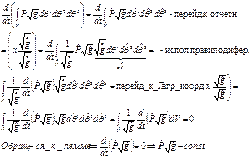
- ур-е неразр. в перем. Лагранжа
Производная по параметру от количества величины в объеме V. Теорема Эйлера. Уравнение неразрывности в переменных Эйлера в интегральной и дифференциальной форме.
1) произв. от кол-ва Pj в объеме V
т.е. 
2) формула Эйлера
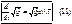
ûjºP, то из (12) 
а в силу сохр. масс, то 
(4) – ур-е Эйлера неразр. в простр коорд. в интегр форме
Закон об изменении количества движения в МСС. Уравнение движения в тензорной форме. Уравнение движения в пространственных декартовых координатах
Постр. закон об изм. движ-я спл-среды
,"V на осн. леммы
- ур-е дв-я сплошной среды
Запишем в частн. случае:
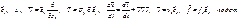
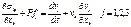
8. Уравнение дв-я сплошн. среды в отчетном базисе:
Каждое слаг-е преопр. в базисе отч. конф:
Введем параметры:
Все разложены по баз. 
, и приравн. один. коэфф.
