ПРАКТИЧЕСКАЯ РАБОТА №1
ТЕМА: «Расчет электрических цепей постоянного тока методом преобразования по законам Ома и Кирхгофа»
Цель работы: изучить и освоить методику расчета электрических цепей постоянного тока методом преобразования по законам Ома и Кирхгофа.
Ход работы
1. Изучить и освоить методику расчета электрических цепей постоянного тока методом преобразования по законам Ома и Кирхгофа (задачи 1 и 2);
2. Записать условия, решение и схемы задач 1 и 2 в тетрадь для лабораторно-практических работ (48 листов);
3. Решить задания для самостоятельной работы (задача 3 и 4);
Сделать вывод по практической работе.
Расчет цепи с одним источником питания
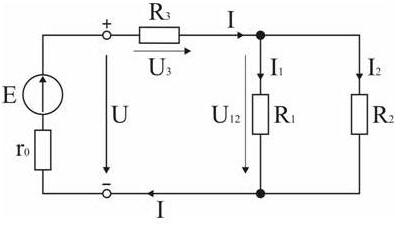
Рисунок к задаче 1.
Задача 1. В цепи, схема которой приведена на рис. 79, ЭДС аккумуляторной батареи Е =78 В, ее внутреннее сопротивление r0 =0,5 Ом. Сопротивления резисторов R 1=10 Ом, R 2=5 Ом, R 3=4 Ом. Вычислить токи во всех ветвях цепи и напряжения на зажимах батареи и на каждом их резисторов.
Анализ и решение задачи 1
1. Обозначение токов и напряжений на участках цепи.
Резистор R 3 включен последовательно с источником, поэтому ток I для них будет общим, токи в резисторах R 1 и R 2 обозначим соответственно I 1 и I 2. Аналогично обозначим напряжения на участках цепи.
2. Определение эквивалентного сопротивления цепи:
R э = r 0 + R 3 + R 1 R 2 / (R 1 + R 2) = 0,5 + 4 + 5 * 10 / (5 +10) = 7,8 Ом
3. Ток в цепи источника рассчитываем по закону Ом а:
I = E / R э = 78 / 7,8 = 10 А
4. Определение напряжений на участках цепи:
U 12 = R 12 I = 3,3 * 10 = 33 В; U 3 = R 3 I = 4 * 10 = 40 В;
U = E - r 0 I = 78 - 0,5 * 10 = 73 В
5. Определение токов и мощностей всех участков:
I 1 = U 12 / R 1 = 33 / 10 = 3,3 А; I 2 = U 12 / R 2 = 33 /5 = 6,6 А;
P 1 = R 1 I 12 = U 12 I 1 = 108,9 Вт; P 2 = R 2 I 22 = U 12 I 2 = 217,8 Вт;
|
|
P 3 = R 3 I 2 = U 3 I = 400 Вт.
Мощность потерь на внутреннем сопротивлении источника:
DP = r 0 I 2 = 50 Вт.
Мощность источника:
P = E I = 780 Вт.
Расчет сложных цепей при помощи уравнений Кирхгофа
Задача 2. Рассчитать схему рис. 80, составив систему уравнений на основании законов Кирхгофа.
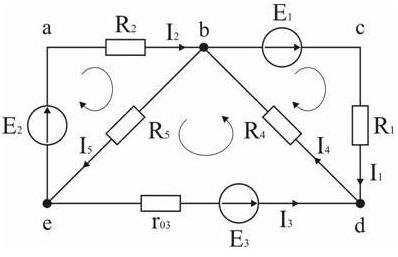
Рисунок к задаче 2.
Исходные данные к задаче:
E 1 = 60 В; E 2 = 80 В; E 3 = 70 В;
R 1 = 20 Ом; R 2 = 50 Ом; r 03 = 5 Ом;
R 4 = 65 Ом; R 5 = 85 Ом.
Анализ и решение задачи 2
1. Определение необходимого числа уравнений.
В схеме рис.80 пять ветвей и для расчета токов в них надо составить пять уравнений. По первому закону Кирхгофа составляются уравнения для всех узлов, кроме одного (уравнение для него будет следствием предыдущих), по второму – для независимых контуров (в каждый последующий контур входит хотя бы одна ветвь, не вошедшая в ранее рассмотренные). Для данной схемы надо составить два уравнения по первому закону и три – по второму.
2. Составление и решение системы уравнений.
Для составления уравнений задаемся произвольно направлениями токов в ветвях и направлениями обхода контуров (рис. 80).
Уравнение для узла d: I 1 + I 3 - I 4 = 0.
Уравнение для узла е: - I 2 - I 3 + I 5 = 0.
Уравнение для контура bcd: I 1 R 1 + I 4 R 4 = E 1.
Уравнение для контура abe: I 2 R 2 + I 5 R 5 = E 2.
Уравнение для контура bde: I 3 r 03 + I 4 R 4 + I 5 R 5 = E 3.
Подставив в уравнения численные значения величин, получим алгебраическую систему уравнений:
I 1 + I 3 - I 4 = 0;
- I 2 - I 3 + I 5 = 0;
20 I 1 + 65 I 4 = 60;
50 I 2 + 85 I 5 = 80;
5 I 3 + 65 I 4 + 85 I 5 = 70.
Решение системы дает значения токов:
I 1=1,093 А; I 2=0,911 А; I 3= –0,506 А; I 4=0,587 А; I 5=0,405 А.
Самостоятельная работа студента
|
|
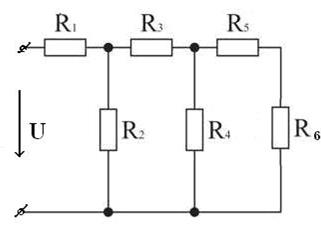
Задача 3. Цепь постоянного тока содержит несколько резисторов, соединенных смешанно рис. 81. Индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на который действует это напряжение. Начертить схему цепи, указать действительные направления токов, проходящих по всем сопротивлениям цепи и определить следующие величины, относящиеся к данной цепи, если они не заданы в условии задачи:
· эквивалентное сопротивление цепи;
· напряжение U, приложенное к цепи;
· ток I на входе цепи;
· токи, проходящие по всем резисторам;
· мощность Р, потребляемую всей цепью.
Дано: R 1 = 8 Ом, R 2 = 6 Ом, R 3 = 4 Ом, R 4 = 2 Ом, R 5 = 4 Ом, R 6 = 2 Ом, I 2 = 2 А
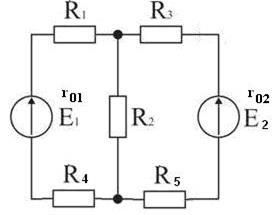
Задача 4. Для электрической цепи, изображенной на рисунке 83, по заданным ЭДС источников постоянного тока (Е) и сопротивлениям ветвей выполнить следующее:
· Определить токи во всех ветвях.
· Определить суммарную мощность, потребляемую цепью.
· Составить уравнение баланса мощностей между источниками и приемниками электроэнергии.
Задачу решить способом контурных токов.
Дано: R 1 = 4 Oм, R 2 = 3 Oм, R 3 = 15 Oм, R 4 = 8 Oм, R 5 = 4 Oм, Е1 = 65 В, r01 = 0,15 Ом, Е2 = 50 В, r02 = 0,1 Ом.