К неполярным относятся диэлектрики, в атомах или молекулах которых центр отрицательно заряженного электронного облака совпадает с центром положительного атомного ядра. Например, инертные газы, кислород, водород, бензол.
Полярные диэлектрики состоят из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Например, спирты, вода. Их молекулы можно рассматривать как совокупность двух точечных зарядов, равных по модулю и противоположных по знаку, находящихся на некотором расстоянии друг от друга. Такую в целом нейтральную систему называют электрическим диполем.
Поляризованность Р – векторная физическаявеличина,равнаяотношению электрическогомомента dp элемента диэлектрика к объему dVэтого элемента и выражаемую в Кл/м2
P=dp/dV.
Диэлектрическая проницаемость вещества – это физическая величина, равная отношению модуля напряженности электрического поля в вакууме к напряженности электрического поля в однородном диэлектрике

Диэлектрическая проницаемость показывает, во сколько раз диэлектрик ослабляет электрическое поле.
31. Проводниками называются тела, способные пропускать через себя электрические заряды. Это свойство проводников объясняется наличием в них свободных носителей заряда. Примерами проводников могут быть металлы и растворы электролитов.
Если взять металлический проводник и один его конец поместить в электрическое поле, то на данном конце появится электрический заряд. Согласно закону сохранения электрического заряда, на другом конце проводника появится равный ему по модулю и противоположный по знаку заряд. Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией. При внесении в электрическое поле проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля внутри проводника становится равной нулю.Свободные заряды перестают перемещаться вдоль поверхности проводящего тела при достижении такого распределения, при котором вектор напряженности электрического поля в любой точке перпендикулярен поверхности тела. Поэтому в электрическом поле поверхность проводника любой формы является эквипотенциальной поверхностью.Электростатическое поле внутри проводника равно нулю, весь статический заряд проводника сосредоточен на его поверхности.
Заряд, сообщенный проводнику, распределится по его поверхности не равномерно. Поверхностной плотностью заряда называется физическая величина, равная отношению заряда к площади, на которой он расположен:

Чем больше кривизна поверхности, тем больше поверхностная плотность заряда. Заряды скапливаются на выступах или остриях.
Уединенным называется проводник, вблизи которого нет других заряженных тел, диэлектриков, которые могли бы повлиять на распределение зарядов данного проводника.
Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью (емкостью) С,  .
.
Таким образом, электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потенциал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его геометрических размеров, формы, диэлектрических свойств окружающей среды и не зависит от величины заряда проводника.
Рассмотрим систему, состоящею из двух проводников, заряды которых равны и противоположны по знаку или один заряжен, а другой нет. Если проводники удалены от других заряженных тел, то разница потенциалов (напряжение) между ними пропорционально заряду. И можно говорить о взаимной емкости двух проводников: 
Взаимная емкость двух проводников зависит от их формы, размеров, взаимного расположения, а также от диэлектрических свойств окружающей их среды
Конденсатор представляет собой систему двух проводников (обкладок) не соединенных друг с другом. Часто между обкладками помещают диэлектрик. Конденсаторы являются накопителями электрических зарядов. Отношение заряда на обкладке конденсатора к разности потенциалов между ними – постоянная величина: q/(j1-j2)=C.
Плоский конденсатор состоит из двух пластин площадью S, расположенных на небольшом расстоянии d друг от друга, заряды на пластинах +q и –q. В общем случае, если пространство между пластинами заполнено диэлектриком с диэлектрической проницаемостью e, то напряженность электростатического поля между пластинами равна сумме напряженности полей создаваемых каждой из пластин.
Е=s/e0e. Емкость плоского конденсатора равна С=e0eS/d.
Параллельное и последовательное соединение конденсаторов. На практике конденсаторы часто соединяют различными способами. Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при тот же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов. При последовательном соединении N конденсаторов заряд на обкладках одинаков, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом конденсаторе в отдельности: Uобщ=U1+U2+U3+...+UN, а общая емкость N конденсаторов 1/Собщ=1/С1+1/С2+1/С3+...+1/СN. При параллельном соединении конденсаторов напряжение U на всех конденсаторах одинаково и общая емкость Собщ батареи равна сумме емкостей отдельных конденсаторов, Собщ=С1+С2+С3+...+СN.
32. Энергия заряженного проводника численно равна работе, которую должны совершить внешние силы для его зарядки W=A. При перенесении заряда dq из бесконечности на проводник совершается работа dA против сил электростатического поля (по преодолению кулоновских сил отталкивания между одноименными зарядами): dA=jdq=Cjdj.
Чтобы зарядить тело от нулевого потенциала до потенциала j, потребуется работа  . Энергия заряженного проводника равна той работе, которую надо совершить, чтобы зарядить его:
. Энергия заряженного проводника равна той работе, которую надо совершить, чтобы зарядить его: 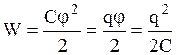 .
.
Выражение  принято называть собственной энергией заряженного проводника.
принято называть собственной энергией заряженного проводника.
Увеличение потенциала j проводника при его зарядке сопровождается усилением электростатического поля, возрастает напряженность поля  . Естественно предположить, что собственная энергия заряженного проводника есть энергия его электростатического поля. Проверим это предположение на примере однородного поля плоского конденсатора. Повторяя ход вышеприведенного расчета, нетрудно получить энергию заряженного плоского конденсатора
. Естественно предположить, что собственная энергия заряженного проводника есть энергия его электростатического поля. Проверим это предположение на примере однородного поля плоского конденсатора. Повторяя ход вышеприведенного расчета, нетрудно получить энергию заряженного плоского конденсатора  ,
,
где  - разность потенциалов его обкладок. Подставим в эту формулу выражения для емкости плоского конденсатора
- разность потенциалов его обкладок. Подставим в эту формулу выражения для емкости плоского конденсатора  и разности потенциалов между обкладками
и разности потенциалов между обкладками  . Тогда для энергии получим
. Тогда для энергии получим  , где V=Sd - объем электростатического поля между обкладками конденсатора.
, где V=Sd - объем электростатического поля между обкладками конденсатора.
Отсюда следует, что собственная энергия заряженного плоского конденсатора пропорциональна V объему его поля и напряженности  . Следовательно, необходимо считать, что электростатическое поле обладает энергией. Объемная плотность энергии электрического поля или энергия единицы объема равна
. Следовательно, необходимо считать, что электростатическое поле обладает энергией. Объемная плотность энергии электрического поля или энергия единицы объема равна  ,
,  . Где же локализована энергия электростатического поля и что является ее носителем - заряды или само поле? Ответ на этот вопрос может дать только опыт. Однако электростатика не может ответить на данный вопрос, потому что она изучает постоянные во времени поля неподвижных зарядов, т.е. в электростатике поля и заряды неотделимы друг от друга.
. Где же локализована энергия электростатического поля и что является ее носителем - заряды или само поле? Ответ на этот вопрос может дать только опыт. Однако электростатика не может ответить на данный вопрос, потому что она изучает постоянные во времени поля неподвижных зарядов, т.е. в электростатике поля и заряды неотделимы друг от друга.
Опыты показали, что переменные во времени электрические поля могут существовать обособленно, независимо от возбудивших их зарядов. Они распространяются в пространстве в виде волн, способных переносить энергию. Отсюда следует, что энергия локализована в поле и носителем электрической энергии является поле.
32. Электрическим током называют упорядоченное (направленное) движение заряженных частиц. Электрический ток возникает при упорядоченном перемещении свободных электронов или ионов.
Сила тока равна отношению заряда Δq, переносимого через поперечное сечение проводника за интервал времени Δt, к этому интервалу времени. Если сила тока со временем не меняется, то ток называют постоянным.
Для постоянного тока 
В соответствии с классической электронной теорией сила тока 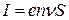 , где е — заряд электрона,
, где е — заряд электрона,  — концентрация свободных электронов в проводнике,
— концентрация свободных электронов в проводнике,  — скорость направленного движения электронов, S — площадь поперечного сечения проводника. Единица силы тока в СИ – А(ампер)
— скорость направленного движения электронов, S — площадь поперечного сечения проводника. Единица силы тока в СИ – А(ампер)
Направление электрического тока в различных точках рассматриваемой поверхности и распределение силы тока по этой поверхности определяются плотностью тока.
Вектор плотности тока j направлен противоположно направлению движения электронов — носителей тока в металлах и численно равен отношению силы тока  через малый элемент поверхности, нормальный к направлению движения заряженных частиц, к величине dS площади этого элемента:
через малый элемент поверхности, нормальный к направлению движения заряженных частиц, к величине dS площади этого элемента:  .
.
Электрический ток возникает под действием электрического поля. При этом равновесное (электростатическое) распределение зарядов в проводнике нарушается, а его поверхность и объем перестают быть эквипотенциальными. Внутри проводника появляется электрическое поле, а касательная составляющая напряженности электрического поля у поверхности проводника 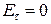 . Электрический ток в проводнике продолжается до тех пор, пока все точки проводника не станут эквипотенциальными. Для того чтобы ток был постоянным во времени, необходимо, чтобы за одинаковые промежутки времени через единицу поверхности протекал одинаковый заряд, т.е. напряженность электрического поля во всех точках проводника, по которому идет этот ток, сохранялась неизменной. Поэтому заряды не должны накапливаться или убывать где-либо в проводнике, по которому идет постоянный ток. В противном случае изменялось бы электрическое поле этих зарядов. Указанное условие означает, что цепь постоянного тока должна быть замкнутой, а сила тока — одинаковой во всех поперечных сечениях цепи.
. Электрический ток в проводнике продолжается до тех пор, пока все точки проводника не станут эквипотенциальными. Для того чтобы ток был постоянным во времени, необходимо, чтобы за одинаковые промежутки времени через единицу поверхности протекал одинаковый заряд, т.е. напряженность электрического поля во всех точках проводника, по которому идет этот ток, сохранялась неизменной. Поэтому заряды не должны накапливаться или убывать где-либо в проводнике, по которому идет постоянный ток. В противном случае изменялось бы электрическое поле этих зарядов. Указанное условие означает, что цепь постоянного тока должна быть замкнутой, а сила тока — одинаковой во всех поперечных сечениях цепи.
Сторонние силы для поддержания тока можно охарактеризовать работой, которую они совершают над зарядами. Величина, равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой(ЭДС)  . ЭДС выражается в вольтах.
. ЭДС выражается в вольтах.
Напряжением (или падением напряжения) 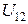 на участке цепи 1—2 называется физическая величина, численно равная работе, совершаемой результирующим полем электростатических и сторонних сил при перемещении вдоль цепи из точки 1 в точку 2 единичного положительного заряда:
на участке цепи 1—2 называется физическая величина, численно равная работе, совершаемой результирующим полем электростатических и сторонних сил при перемещении вдоль цепи из точки 1 в точку 2 единичного положительного заряда:  .
.
При отсутствии сторонних сил напряжение U совпадает с разностью потенциалов.
34.
 Рис.1 Рис.1
| Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а j1 и j2 – потенциалы на концах проводника (рис1). В случае однородного проводника величину j1 - j2 = U можно назвать падением напряжения на участке проводника. |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:
 (1)где R – электрическое сопротивление проводника.
(1)где R – электрическое сопротивление проводника.
(1) – закон Ома в интегральной форме.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника  (2),где R - удельное сопротивление проводника.
(2),где R - удельное сопротивление проводника.
я в СИ: [R] = Ом×м.
Величина, обратная сопротивлению, называется проводимостью.Величина, обратная удельному сопротивлению, называется удельной проводимостью: 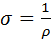 (3)
(3)
Единица, обратная Ом, называется Сименсом [См].
Учитывая (1) - (3), а также  , получим:
, получим:


 (3.50)
(3.50)
(3.50) – закон Ома в дифференциальной форме.
35. Электрического тока в вакууме нет, т.к. в термодинамическом вакууме отсутствуют какие-либо частицы.
Однако наилучший достигнутый практически вакуум составляет

 ,
,
т.е. огромное количество частиц.
Тем не менее, когда говорят о токе в вакууме, подразумевают идеальный в термодинамическом смысле вакуум, т.е. полное отсутствие частиц. За протекание тока отвечают частицы, полученные из какого-либо источника.
Термоэлектро́нная эми́ссия — явление выбивания электронов из металла при высокой температуре. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растёт, и явление термоэлектронной эмиссии становится заметным.
Газы, в отличие от металлов и электролитов, состоят из электрически нейтральных атомов и молекул и в нормальных условиях не содержат свободных носителей тока (электронов и ионов). Поэтому газы в нормальных условиях являются диэлектриками.
Носители электрического тока в газах могут возникнуть только в процессе ионизации газов, т.е. в процессе образования ионов в газе.
Процесс ионизации газов происходит под влиянием внешних воздействий (внешних ионизаторов): сильного нагревания, ультра-фиолетовых и рентгеновских лучей.
Процесс ионизации газов происходит следующим образом.
1. Под влиянием внешних факторов электроны отрываются от атомов или молекул. При этом атомы (молекулы) газов превращаются в положительные ионы.
2. Отрицательные ионы в газах могут возникнуть, если атомы (молекулы) присоединяют к себе электроны.
Мерой ионизации газов является интенсивность ионизации, измеряемая числом пар противоположно заряженных частиц, возникающих в единице объёма газа за единицу времени.
Противоположным процессу ионизации газов является процесс рекомбинации.
Процесс рекомбинации газов происходит следующим образом.
1. Положительные и отрицательные ионы могут при соударениях нейтрализовать друг друга, образуя обычные нейтральные молекулы.
2. При сближении электрона и положительного иона они могут вновь объединяться в нейтральный атом.
Электрический ток в газах называется газовым разрядом.
Газовый разряд бывает двух видов:
1. Самостоятельный газовый разряд.
2. Несамостоятельный газовый разряд.
Виды самостоятельного разряда:
Искровой разряд.
Примеры искрового разряда – искры, возникающие при расчёсывании волос, при разрядке конденсатора.
Дуговой разряд.
Для резки и сварки металлических конструкций, для плавки металлов используют высокую температуру плазмы дугового разряда.
Тлеющий разряд
В настоящее время трубки с тлеющим разрядом находят практическое применение как источник света – газоразрядные лампы.
Коронный разряд
Используется световое излучение ламп дневного света, газоразрядных ламп уличного освещения; электрическая дуга применяется в кинопроекционном аппарате; ртутно-кварцевая лампа нашла применение в поликлиниках и больницах.
36. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения; магнитная составляющая электромагнитного поля.
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).
Кроме этого, оно возникает в результате изменения во времени электрического поля.
Магнитная индукция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд
магнитное поле действует на заряд  , движущийся со скоростью
, движущийся со скоростью  . Направление линий магнитной индукции - определяется по правилу буравчика или по правилу правой руки.
. Направление линий магнитной индукции - определяется по правилу буравчика или по правилу правой руки.
Правило буравчика (в основном для прямого проводника с током): Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока. Правило правой руки (в основном для определения направления магнитных линий внутри соленоида):Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.
 Магнитная индукция поля постоянного электрического тока, созданная элементом
Магнитная индукция поля постоянного электрического тока, созданная элементом  линейного проводника с током I в вакууме, удовлетворяет закону Био-Савара_Лапласа, который в СИ имеет вид:
линейного проводника с током I в вакууме, удовлетворяет закону Био-Савара_Лапласа, который в СИ имеет вид:  , где
, где  - плотность тока;
- плотность тока; 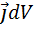 и
и 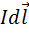 – соответственно объемный и линейный элемен тока;
– соответственно объемный и линейный элемен тока; 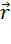 – радиус-вектор, проведенный из элемента
– радиус-вектор, проведенный из элемента  в рассматриваемую точу. Применение к расчету магнитного поля кругового витка. Определим магнитную индукцию поля витка с током I в произвольной точке на оси витка
в рассматриваемую точу. Применение к расчету магнитного поля кругового витка. Определим магнитную индукцию поля витка с током I в произвольной точке на оси витка  . Проходящей через центр витка перпендикулярного его плоскости. На рисунке показан круговой виток радиус R, плоскость перпендикулярна плоскости чертежа, а ось
. Проходящей через центр витка перпендикулярного его плоскости. На рисунке показан круговой виток радиус R, плоскость перпендикулярна плоскости чертежа, а ось  лежит в эой плоскоси. В точке А н оси
лежит в эой плоскоси. В точке А н оси  векторы
векторы  для полей различных малых элементов
для полей различных малых элементов  витка с током не совпадают по направлению. Векторы
витка с током не совпадают по направлению. Векторы  и
и  для полей двух диаметрально противоположных элементов витка
для полей двух диаметрально противоположных элементов витка  и
и  , имеющих одинаковую длину
, имеющих одинаковую длину  , равны по модулю
, равны по модулю  , так как (
, так как ( )=
)=  . Результирующий вектор
. Результирующий вектор  направлен в точке А по оси витка, причем
направлен в точке А по оси витка, причем  . Таким образом, поперечные составляющие
. Таким образом, поперечные составляющие  взаимно компенсирую друг друга. Вектор индукции
взаимно компенсирую друг друга. Вектор индукции  в точке А для магнитного поля всего витка направлен также вдоль оси
в точке А для магнитного поля всего витка направлен также вдоль оси  , а его модуль определяется так:
, а его модуль определяется так:  . Учитывая, что
. Учитывая, что  ,получаем
,получаем

|
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита. Величину магнитного момента кругового витка с током можно определить по формуле.
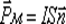
Где, I ток протекающий по витку
S площадь витка с током
n нормаль к плоскости в которой находится виток
Таким образом, из формулы видно, что магнитный момент витка это векторная величина. То есть кроме величины силы, то есть ее модуля он обладает еще и направлением.
37. Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника: 
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока – ампера.

|
Пусть в однородное магнитное поле помещена рамка с током (рис.). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором  и нормалью к площади
и нормалью к площади  :
:
 . Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке. Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:
. Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке. Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:  .Это выражение также можно использовать для определения индукции магнитного поля:
.Это выражение также можно использовать для определения индукции магнитного поля:  .
.
Величину, равную произведению  , называют магнитным моментом контура Рт. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать
, называют магнитным моментом контура Рт. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать 
38. Закон о циркуляции вектора  : циркуляция вектора
: циркуляция вектора  по произвольному контуру Lравна произведению
по произвольному контуру Lравна произведению 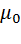 на алгебраическую сумму токов, охватываемых данным контуром:
на алгебраическую сумму токов, охватываемых данным контуром:  , где
, где  =
=  - элемент длины контура, направленный вдоль обхода контура;
- элемент длины контура, направленный вдоль обхода контура;  - вектор касательной в данной точке к контуру;
- вектор касательной в данной точке к контуру;  - составляющая вектора
- составляющая вектора  в направлении касательной к контуру с учетом выбранного направления обхода; n- число проводников с током, охватываемых контуром L произвольной формы.
в направлении касательной к контуру с учетом выбранного направления обхода; n- число проводников с током, охватываемых контуром L произвольной формы.
Применение этого закона к расчету магнитного поля прямого тока. Формула  для индукции магнитного поля тонкого прямолинейного бесконечного проводника с током дает некорректный результат при
для индукции магнитного поля тонкого прямолинейного бесконечного проводника с током дает некорректный результат при  , т.е. на оси проводника получаем В→∞. Учтем, что реальный проводник имеет конечное поперечное сечение R и используем хакон циркуляции вектора магнитной индуции.
, т.е. на оси проводника получаем В→∞. Учтем, что реальный проводник имеет конечное поперечное сечение R и используем хакон циркуляции вектора магнитной индуции.
Пусть постоянный токI течет вдоль бесконечно длинного прямого провода. Замкнуты контур L представим в виде окружности радиуса r.Из симметрии задачи следует, что линии вектора  имеют вид окружностей с центром на оси провода. Модуль вектора
имеют вид окружностей с центром на оси провода. Модуль вектора  должен быть одинаков во всех точках на расстоянии rот оси провода. Вектор
должен быть одинаков во всех точках на расстоянии rот оси провода. Вектор  направлен по касательной к окружности:
направлен по касательной к окружности:  , где
, где 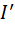 - ток, охватываемый контуром L. Вне проводника с током (r>R) получаем результат, совпадающий с ранее полученной формулой
- ток, охватываемый контуром L. Вне проводника с током (r>R) получаем результат, совпадающий с ранее полученной формулой  , так как
, так как 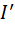 =
=  и
и  .Таким образом, на оси проводника с током В=0. Магнитное поле имеет наибольшую индукцию на поверхности проводника.
.Таким образом, на оси проводника с током В=0. Магнитное поле имеет наибольшую индукцию на поверхности проводника.
39. Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:  .Сила Ампера равна
.Сила Ампера равна  , сила тока равна
, сила тока равна  Подставив эти выражения в формулу для силы Лоренца, получим:
Подставив эти выражения в формулу для силы Лоренца, получим:
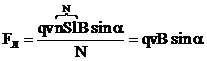
где  - угол между векторами скорости и магнитной индукции.
- угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
40. Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.
Формула магнитного потока:
Ф = BS cos α, здесь α - угол между направлением вектора магнитной индукции B и нормалью к поверхности S.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с.
Теорема Остроградского-Гаусса для магнитного потока является обобщением опытных фактов:
магнитный поток через любую замкнутую поверхность равен 0 .

Это означает, что силовые линии магнитного поля замкнуты, и в природе не существует магнитных зарядов — источников магнитного поля, из которых могли бы исходить силовые линии или на которых они обрывались бы. Источниками магнитного поля являются токи, и силовые линии магнитного поля замыкаются вокруг них.
 , ,
|
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
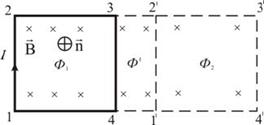 Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток
Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток  , пронизывающий контур, направлен по нормали
, пронизывающий контур, направлен по нормали  к контуру, поэтому
к контуру, поэтому  .
.
Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком  .
.
Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком  .
.
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
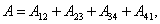
где  ,
,  равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
 .
.
Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля.
), но движется против сил действия магнитного поля.
 .
.
Тогда общая работа по перемещению контура
 или
или
 , ,
| ( |
здесь  – это изменение магнитного потока, сцепленного с контуром.
– это изменение магнитного потока, сцепленного с контуром.
41. Возникновение эдс в замкнутом проводящем контуре при изменении магнитного потока через эту поверхность, ограниченную этим контуром, называется электромагнитной индукцией. Также эдс индукции, а следовательно, разность потенциалов возникает на концах разомкнутого проводника, движущегося в магнитном поле и пересекающего силовые линии поля. Опыт показывает, что эдс индукции не зависит от причин измения магнитного потока, а определяется скоростью его изменения. Согласно закону Фарадея, эдс индукции определяется как предел отношения изменения магнитного потока DФ к промежутку времени Dt к нулю, или производной по времени магнитного потока 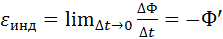
Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура. По правилу Ленца, Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.
Явление ЭИ находит широкое применение в технике. Оно используется в индукционных генераторах тока, индукционных плавильных печах, трансформаторах, в счетчиках электроэнергии и др.
Закон ЭИ формулируется именно для ЭДС индукции, а не для силы индукционного тока: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:  С учетом правила Ленца:
С учетом правила Ленца:  . При изменении магнитного потока в катушке, имеющей n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС одного витка.
. При изменении магнитного потока в катушке, имеющей n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС одного витка.
42. Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток через контур из этого проводника пропорционален модулю индукции магнитного поля внутри контура, а индукция магнитного поля в свою очередь пропорциональна силе тока в проводнике. Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Коэффициент пропорциональности между силой тока в контуре и магнитным потоком, создаваемым этим током, называется индуктивностью. Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
За единицу индуктивности в Международной системе принимается генри. Индуктивность контура равна 1 Гн,
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного поля, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке. Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой цепи называется самоиндукцией.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
ЭДС самоиндукции, возникающая в катушке, по закону электромагнитной индукции равна
 , т. е.
, т. е. 
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Элемент электрической цепи обладает индуктивностью 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.
При всяком изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции Экстратоки самоиндукции, согласно правилу Ленца, направлены гак, чтобы препятствовать изменениям тока в цепи, т.е. направлены противоположно току, создаваемому источником. При включении источника тока экстратоки имеют такое же направление, что и ослабевающий ток.  (1)
(1)
где  - постоянная, называемая временем релаксации. Из (1) следует, что т есть время, в течение которого сила тока уменьшается в е раз.
- постоянная, называемая временем релаксации. Из (1) следует, что т есть время, в течение которого сила тока уменьшается в е раз.
 Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспонен
Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспонен