Двусвязные компоненты
Задан связный неориентированный граф  .
.
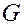 является двусвязным, если он остается связным при выбрасывании любой его вершины с инцидентными ребрами.
является двусвязным, если он остается связным при выбрасывании любой его вершины с инцидентными ребрами.
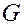 содержит т очку сочленения
содержит т очку сочленения  , если для некоторой пары вершин
, если для некоторой пары вершин  и
и  все пути из
все пути из  в
в  проходят через
проходят через  .
.
Удаление точки сочленения (точки разрыва) разбивает граф, по крайней мере, на 2 несвязные части.
 |
На мн-ве ребер  графа
графа 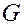 можно определить отношение эквивалентности:
можно определить отношение эквивалентности:  , если
, если  или оба ребра лежат в одном цикле.
или оба ребра лежат в одном цикле.
Пусть  – классы эквивалентности (
– классы эквивалентности ( ) и
) и  – соответствующие им множества вершин. Тогда
– соответствующие им множества вершин. Тогда  – это двусвязные компоненты
– это двусвязные компоненты 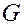 .
.
Лемма, определяющая двусвязные компоненты, точки сочленения и их свойства (Ахо):
1. Графы  – двусвязные
– двусвязные  .
.
2.  мн-во
мн-во  содержит не более одной вершины.
содержит не более одной вершины.
3.  – точка сочленения
– точка сочленения 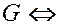
 для некоторых
для некоторых  .
.
=> Точки сочленения разделяют двусвязные компоненты.
Лемма (Ахо). Пусть построено глубинное остовное дерево. Вершина  будет точкой сочленения тогда и только тогда, когда выполняется одно из условий:
будет точкой сочленения тогда и только тогда, когда выполняется одно из условий:
1.  – корень и имеет более 1 сына (поддеревья
– корень и имеет более 1 сына (поддеревья  связаны только через
связаны только через  ).
).
2.  – не корень и для некоторого его сына
– не корень и для некоторого его сына  нет обратных ребер, соединяющих
нет обратных ребер, соединяющих  и\или ее потомков с предками
и\или ее потомков с предками  .
.
 |
Пусть при поиске в глубину вершинам присвоена новая нумерация в порядке их обхода. Тогда, если  – потомок
– потомок  ,
,  – обратное ребро и
– обратное ребро и  , то
, то  – предок
– предок  .
.
Определим функцию «нижний» 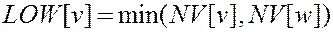 :
:
 обратное ребро
обратное ребро  , где
, где  – потомок
– потомок  (или
(или  ), а
), а  – предок
– предок  (не отец при
(не отец при  , т.к.
, т.к.  – обратное ребро).
– обратное ребро).
 |
(На рисунке значения 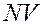 – черные,
– черные,  – красные).
– красные).
Значения функции  нужно определять рекурсивно, вместе с поиском в глубину, как минимальное из 3 значений:
нужно определять рекурсивно, вместе с поиском в глубину, как минимальное из 3 значений:
1.  (начальное значение).
(начальное значение).
2.  , где
, где  – сын
– сын  .
.
3.  , если
, если  обратное ребро
обратное ребро  .
.
Следствие последней леммы:
 – не корень и точка сочленения
– не корень и точка сочленения 
 , где
, где  – сын
– сын  .
.
При поиске в глубину будем помещать все выделенные ребра (древесные и обратные) в стек и выталкивать оттуда мн-ва ребер, принадлежащих отдельным двусвязным компонентам. Для этого достаточно при рекурсивном подъеме находить древесные ребра  , для которых
, для которых  : все ребра от
: все ребра от  и выше в стеке
и выше в стеке  одной компоненте.
одной компоненте.
В программе ниже используются массивы:
Old[n] – старая или новая (непроверенная) вершина,
NV[n] – новый номер вершины,
Low[n] – значения функции,
Fath[n] – номера вершин-отцов.
Граф задан списками смежных вершин L[n].
Подготовка массивов, выделение корней глубинных остовных деревьев (для отдельных компонент связности), вызов рекурсивной функции поиска в глубину:
dcomp = 0; newnum = 0;
for (k = 0; k < n; k++) {
Old[k] = false; Fath[k] = -1;
}
for (k = 0; k < n; k++)
if (!Old[k]) search2(k);
Поиск в глубину с выделением двусвязных компонент:
void search2(int v) {
Old[v] = true; Low[v] = NV[v] = ++newnum;
for (w  L[v])
L[v])
if (Old[w] == 0) { // (v,w) - древесное
push(v, w); Fath[w] = v; search2(w);
if (Low[w]>=NV[v]) {dcomp++; //v – ТС
do rib=pop(); добавить(rib, dcomp);
while (rib!= (v,w));
} Low[v] = min(Low[v], Low[w]);
}
else if (NV[w]<NV[v] && w!=Fath[v]) { // обр
push(v,w); Low[v] = min(Low[w], NV[w]);
}
}
Трудоемкость данного алгоритма составляет  .
.
Сильно связные компоненты
Задан ориентированный граф  . Для него могут быть определены компоненты трех типов, в зависимости от условий связности произвольной пары вершин
. Для него могут быть определены компоненты трех типов, в зависимости от условий связности произвольной пары вершин  и
и  , принадлежащих одной компоненте:
, принадлежащих одной компоненте:
1. Слабо связные – из  и
и  существует маршрут, если все дуги
существует маршрут, если все дуги 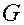 заменить на ребра.
заменить на ребра.
2. Односторонние – существует либо путь из  в
в  , либо из
, либо из  в
в  , либо оба вместе.
, либо оба вместе.
3. Сильно связные – существуют пути из  в
в  и обратно (т.е. цикл, образованный дугами).
и обратно (т.е. цикл, образованный дугами).
Слабо связные компоненты можно найти поиском в глубину на графе, в котором все дуги заменены ребрами.
Односторонние можно выделить с помощью построения и объединения глубинных остовных деревьев со всеми возможными корневыми вершинами.
На множестве вершин  можно определить отношение эквивалентности:
можно определить отношение эквивалентности: 

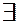 пути из
пути из  в
в  и обратно.
и обратно.
Пусть  – классы эквивалентности, а
– классы эквивалентности, а  – множества дуг, соединяющих вершины
– множества дуг, соединяющих вершины  . Тогда
. Тогда  – сильно связные компоненты
– сильно связные компоненты 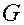 .
.
1-й алгоритм выделения ССК (1 поиск в глубину, Ахо)
При поиске в глубину на орграфе образуются 4 типа дуг:
1. Древесные.
2. Прямые – от предков к потомкам (не древесные).
3. Обратные – от потомков к предкам.
4. Поперечные – соединяют вершины, не являющиеся предками и потомками друг друга.
(на рисунке: 1 – синие, 2 – зеленые, 3 – красные, 4 – розовые; цифры – номера вершин в порядке обхода в глубину).
 |
Лемма: если  – поперечная дуга, то
– поперечная дуга, то  .
.
Док-во:
1.  ведет в уже пройденную вершину
ведет в уже пройденную вершину  , иначе эта дуга была бы древесной.
, иначе эта дуга была бы древесной.
2. Если проверяется дуга  , то поиск в глубину из вершины
, то поиск в глубину из вершины  пока не закончен (необходимо проверить все возможные пути из
пока не закончен (необходимо проверить все возможные пути из  ). Пусть
). Пусть  была пройдена раньше, чем
была пройдена раньше, чем  , т.е.
, т.е.  . Это возможно только в том случае, когда
. Это возможно только в том случае, когда  лежит на некотором пути из
лежит на некотором пути из  (состоящем из древесных дуг), но тогда дуга
(состоящем из древесных дуг), но тогда дуга  – прямая.
– прямая.
Основная лемма об ССК (без док-ва, Ахо):
Пусть  – ССК, а
– ССК, а  – глубинный остовный лес на
– глубинный остовный лес на  . Тогда вершины
. Тогда вершины  вместе с дугами, входящими в
вместе с дугами, входящими в  , образуют дерево.
, образуют дерево.
Следствие:
- любые вершины  имеют общего предка;
имеют общего предка;
- предок  с минимальным номером, присвоенным при поиске, является корнем дерева (и однозначно определяет дерево).
с минимальным номером, присвоенным при поиске, является корнем дерева (и однозначно определяет дерево).
Если перенумеровать  в том порядке, в каком для
в том порядке, в каком для  заканчивается поиск в глубину (т.е., сначала
заканчивается поиск в глубину (т.е., сначала  , затем
, затем  ,…), то выполняется следующая
,…), то выполняется следующая
Лемма: 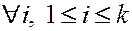 граф
граф  состоит из вершин, являющихся потомками
состоит из вершин, являющихся потомками  и не принадлежащих ни одному из
и не принадлежащих ни одному из  .
.
Практическое следствие: при поиске в глубину будем помещать вершины в стек в порядке их обхода; при обнаружении корня  какой-либо ССК вытолкнем из стека все вершины до
какой-либо ССК вытолкнем из стека все вершины до  включительно – все они принадлежат одной ССК.
включительно – все они принадлежат одной ССК.
Каждая вершина принадлежит только одной ССК, но могут существовать дуги, соединяющие вершины из разных ССК.
Рассмотрим ССК 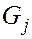 и
и 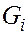 , где
, где 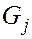 выделяется раньше, чем
выделяется раньше, чем  .
.
 |
Варианты соединений:
1. 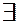 обе дуги –
обе дуги –  и
и  . Невозможен, т.к. в этом случае
. Невозможен, т.к. в этом случае  образуют одну ССК.
образуют одну ССК.
2. 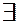 только дуга
только дуга  . Поиск для
. Поиск для 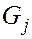 не закончится, пока не будут проверены все возможные пути из ее вершин, в том числе и включающие дугу
не закончится, пока не будут проверены все возможные пути из ее вершин, в том числе и включающие дугу  . Поэтому
. Поэтому  не может быть выделена раньше, чем
не может быть выделена раньше, чем 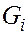 .
.
3. 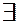 только дуга
только дуга  . Если по этой дуге мы впервые приходим в
. Если по этой дуге мы впервые приходим в 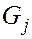 , то
, то  будет древесной дугой, а
будет древесной дугой, а  корнем дерева
корнем дерева  . В противном случае ССК
. В противном случае ССК  уже выделена (ее вершины вытолкнуты из стека) и поперечную дугу
уже выделена (ее вершины вытолкнуты из стека) и поперечную дугу  вообще не нужно обрабатывать.
вообще не нужно обрабатывать.
Пути, состоящие из древесных дуг, ведут от предков к потомкам в дереве.
Прямые дуги просто дублируют участки путей на дереве, поэтому их можно вообще не рассматривать.
Пути от потомков к предкам в дереве определяют обратные и, потенциально, поперечные дуги.
Пусть 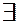 поперечная дуга
поперечная дуга  , где
, где 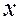 – потомок
– потомок 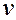 или
или 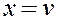 . Если
. Если 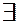 обратная дуга
обратная дуга  , где
, где  – потомок
– потомок  или
или  , а
, а  – предок
– предок  , то вершины
, то вершины  принадлежат одной ССК.
принадлежат одной ССК.
 |
Для каждой вершины  нужно найти ее предка
нужно найти ее предка  , достижимого из
, достижимого из  по путям, содержащим обратные и поперечные дуги, и имеющего минимальный номер
по путям, содержащим обратные и поперечные дуги, и имеющего минимальный номер 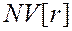 – это корень ССК, содержащей
– это корень ССК, содержащей  .
.
Введем функцию «нижняя связь»
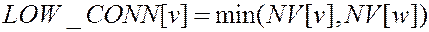 :
:  поперечная или обратная дуга из
поперечная или обратная дуга из  или некоторого потомка
или некоторого потомка 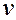 в вершину
в вершину  , причем корень ССК, к-рая содержит
, причем корень ССК, к-рая содержит  , является предком
, является предком 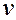 .
.
Лемма:
 явл-ся корнем ССК
явл-ся корнем ССК 
 .
.
В приведенной ниже программе используется стек для выделения вершин ССК.
Значения  вычисляются рекурсивно в массиве LCon.
вычисляются рекурсивно в массиве LCon.
Для того, чтобы не учитывать поперечные дуги, соединяющие разные ССК, исп-ся массив InS: InS[v] = 1, если v – в стеке.
Подготовка массивов, выделение корней глубинных остовных деревьев, вызов рекурсивной функции поиска в глубину:
sccomp = 0; newnum = 0;
for (k = 1; k <= n; k++) {
Old[k] = 0; InS[k] = 0;
}
for (k = 1; k <= n; k++)
if (Old[k] == 0) search_SCC(k);
Поиск в глубину с выделением ССК:
void search_SCC(int v) { Old[v]=1;
LCon[v]=NV[v]=++newnum; push(v); InS[v]=1;
for (w  L[v])
L[v])
if (Old[w] == 0) { // (v,w) - древесная
search_SCC(w);LCon[v]=min(LCon[v],LCon[w]);
}
else if (NV[w]<NV[v] && InS[w]==1) // О\П
LCon[v] = min(LCon[v], NV[w]);
if (LCon[v] == NV[v]) { sccomp++; //v–корень ССК
do x = pop(); InS[x] = 0;
сохранить_вершину(x, sccomp);
while (x!= v);
}
}
Трудоемкость данного алгоритма составляет 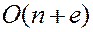 .
.
Следующий рисунок иллюстрирует результаты работы алгоритма поиска в глубину с расчетом новых номеров NV и значений LCon (красные цифры).
При вычислении значений LCon не учитывались поперечные дуги, ведущие в вершины уже выделенных ССК (удаленные из стека).

2-й алгоритм выделения ССК (Кормен)
Данный алгоритм использует поиск в глубину дважды.
При 1-м поиске для каждой вершины вычисляется ее новый номер, но не в порядке прихода в нее ( ), а в порядке завершения поиска (завершения проверки всех дуг, исходящих из данной вершины) –
), а в порядке завершения поиска (завершения проверки всех дуг, исходящих из данной вершины) –  .
.
После этого исходный граф  «транспонируется», т.е. в нем изменяется направление всех дуг. В результате получается граф
«транспонируется», т.е. в нем изменяется направление всех дуг. В результате получается граф  :
:  .
.
Далее проводится поиск в глубину на  , причем вершины выбираются в порядке убывания значений
, причем вершины выбираются в порядке убывания значений  , вычисленных при 1-м поиске. Полученные на данном шаге глубинные остовные деревья соответствуют сильно связным компонентам исходного графа
, вычисленных при 1-м поиске. Полученные на данном шаге глубинные остовные деревья соответствуют сильно связным компонентам исходного графа  .
.
Поиск в глубину с вычислением значений LV:
lastnum = 0; // тек. значение номера
for (k = 1; k <= n; k++) Old[k] = 0;
for (k = 1; k <= n; k++)
if (Old[k] == 0) search(k);
void search(int v) {
Old[v] = 1;
for (w  L[v])
L[v])
if (Old[w] == 0) search(w);
LV[v] = ++lastnum;
}
Иллюстрация работы предыдущего алгоритма (древесные дуги синие, для вершин указаны значения  ):
):
 |
Исходный порядок выбора вершин:  .
.
Порядок первого прихода в вершину:  .
.
Пусть  – произвольная пара вершин
– произвольная пара вершин  . Очевидно, что
. Очевидно, что  достижима из
достижима из  на графе
на графе  , тогда и только тогда, когда
, тогда и только тогда, когда  достижима из
достижима из  на
на  . Поэтому графы
. Поэтому графы  и
и  содержат одни и те же сильно связные компоненты (точнее, мн-ва вершин, образующих ССК).
содержат одни и те же сильно связные компоненты (точнее, мн-ва вершин, образующих ССК).
При поиске в глубину все вершины одной ССК образуют одно дерево, т.е. имеют одного общего предка (основная лемма).
Дерево любой ССК является поддеревом некоторого глубинного дерева, и каждая вершина графа принадлежит какой-либо ССК. Поэтому корни глубинных деревьев являются также корнями ССК.
Выберем вершину с максимальным значением 
 :
:  .
.
 – последняя вершина
– последняя вершина  , в к-рой закончился поиск в глубину, следовательно,
, в к-рой закончился поиск в глубину, следовательно,  – это корень некоторого глубинного дерева (и корень некоторой ССК). Любая вершина этого дерева достижима из
– это корень некоторого глубинного дерева (и корень некоторой ССК). Любая вершина этого дерева достижима из  на графе
на графе  .
.
Проведем поиск в глубину на «транспонированном» графе  , начав с вершины
, начав с вершины  . Очевидно, что
. Очевидно, что  будет корнем некоторого глубинного дерева со мн-вом вершин
будет корнем некоторого глубинного дерева со мн-вом вершин 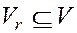 .
.
Любая вершина  будет достижима из
будет достижима из  на
на  , т.е.
, т.е.  достижима из
достижима из  на исходном графе
на исходном графе  .
.
Предположим, что  такая вершина
такая вершина  , что
, что  недостижима из
недостижима из  на
на  .
.
Тогда  и
и  должны принадлежать разным глубинным деревьям
должны принадлежать разным глубинным деревьям  и
и  на графе
на графе  .
.
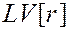 является максимальным среди значений
является максимальным среди значений  , следовательно, построение
, следовательно, построение  началось и закончилось раньше, чем
началось и закончилось раньше, чем  .
.
Но построение  не может закончиться, пока не проверены связи всех его вершин, а
не может закончиться, пока не проверены связи всех его вершин, а  достижима из
достижима из  , т.е.
, т.е.  должна принадлежать
должна принадлежать  – противоречие.
– противоречие.
Следовательно, все вершины  достижимы из
достижимы из  и наоборот, т.е.
и наоборот, т.е.  – это мн-во вершин одной ССК.
– это мн-во вершин одной ССК.
При поиске в глубину на  будем помещать все пройденные вершины в стек и отмечать, как проверенные.
будем помещать все пройденные вершины в стек и отмечать, как проверенные.
После выделения  (проверки всех связей вершины
(проверки всех связей вершины  ) нужно вытолкнуть полученные вершины из стека и продолжить поиск в глубину, начиная с непроверенной вершины, имеющей максимальное значение
) нужно вытолкнуть полученные вершины из стека и продолжить поиск в глубину, начиная с непроверенной вершины, имеющей максимальное значение  . Очередное выделенное дерево будет содержать все вершины следующей ССК.
. Очередное выделенное дерево будет содержать все вершины следующей ССК.
Таким образом, от графа будут последовательно «отщепляться» сильно связные компоненты.
Общая трудоемкость алгоритма составляет  , если используются списки смежных вершин, или
, если используются списки смежных вершин, или  – для матрицы смежности.
– для матрицы смежности.
Иллюстрация работы алгоритма поиска в глубину на графе  . Вершины выбирались в порядке убывания значений
. Вершины выбирались в порядке убывания значений  :
:  .
.

Выделено 3 ССК со мн-вами вершин:  ,
,  ,
,  .
.