МЕТОДОМ КОМПЕНСАЦИИ
Цель работы: изучить компенсационный метод измерения ЭДС источника тока. Измерить ЭДС.
Приборы и оборудование: установка для измерения ЭДС источника тока методом компенсации или лабораторный стенд.
Теоретические сведения
Электрическим током называется направленное движение электрических зарядов. Электрический ток принято характеризовать силой тока - скалярной величиной, равной заряду, проходящему через поперечное сечение проводника за единицу времени. Единица силы тока - ампер (А):
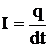 (1)
(1)
Если за любые равные промежутки времени через поперечное сечение проводника проходит одинаковое количество электричества, то такой ток называется постоянным.
За направление тока принимается направление движения положительных зарядов.
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется его плотностью:
 (2)
(2)
Плотность тока - вектор. Направление вектора 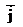 совпадает с направлением упорядоченного движения положительных зарядов.
совпадает с направлением упорядоченного движения положительных зарядов.
В 1826 г. Г.С.Ом экспериментально установил, что сила тока в однородном проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника:
 (3)
(3)
где U - напряжение на концах проводника; R - сопротивление проводника.
Сопротивление зависит от материала, из которого изготовлен проводник, его линейных размеров и формы:
 (4)
(4)
где U - удельное электрическое сопротивление; l - длина проводника; S -площадь сечения. При этом ρ - коэффициент пропорциональности, характеризующий материал проводника. За его единицу в системе СИ принимается сопротивление провода длиной 1м и площадью сечения 1 м2. Единица удельного электрического сопротивления - ом; - метр (Ом-м). 1 Ом·м - это удельное электрическое сопротивление проводника, имеющего электрическое сопротивление 1Oм при длине 1м и площади поперечного сечения 1м2.
Опыт показывает, что зависимость удельного сопротивления (а следовательно, и сопротивления) и температуры описывается линейным законом
pt=p0(1 + αt°);
Rt=R0(1 + αt°), (5)
где ρt и ρо, Rt и ro - соответственно удельные электрические сопротивления и сопротивления проводника при температурах t°C и 0°С; α - температурный коэффициент сопротивления.
При температурах, близких абсолютному нулю (-273°С), сопротивление, многих проводников также стремится к нулю, т.е. проводник переходит в сверхпроводящее состояние.
Если в выражение (3) подставить (4) и учесть, что
 (6)
(6)
где Е - напряженность поля внутри проводника, получим закон Ома в дифференциальной форме:
 (7)
(7)
где  - удельная электрическая проводимость материала проводника (γ). Единица ее измерения - сименс на метр (См/м). Учитывая, что
- удельная электрическая проводимость материала проводника (γ). Единица ее измерения - сименс на метр (См/м). Учитывая, что  - напряженность
- напряженность
электрического поля в проводнике (Е), а  плотность тока (j), то
плотность тока (j), то
j = γE. (8)
Так как носители заряда в каждой точке движутся в направлении вектора  , то направления
, то направления 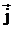 и
и  совпадают. Поэтому формулу j = γE можно записать в векторном виде:
совпадают. Поэтому формулу j = γE можно записать в векторном виде:
 (8)
(8)
Это выражение закона Ома в дифференциальной форме.
Для того чтобы поддержать ток в проводнике достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда считаем положительными) непрерывно отводить приносимые заряды, а к концу с бóльшим потенциалом непрерывно их подводить, т.е. необходимо установить круговорот зарядов, при котором они двигались бы по замкнутой траектории.
В замкнутой цепи имеются участки, на которых заряды движутся в сторону возрастания потенциала, т.е. против электростатического поля. Перемещение зарядов на них возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо по всей цепи, либо на отдельных участках. Они могут быть обусловлены химическими, диффузионными процессами, переменными магнитными полями и т.д.
Основной характеристикой сторонних сил является их электродвижущая сила, ЭДС, т.е. физическая величина, численно равная работе сторонних сил по перемещению единичного заряда. Из определения ЭДС следует, что
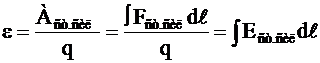 (9)
(9)
где  - напряженность поля сторонних сил.
- напряженность поля сторонних сил.
Из формулы (9) видно, что размерность ε совпадает с размерностью потенциала и измеряется в системе СИ в вольтах (В).
Если источник тока замкнуть на внешнюю нагрузку, равномерно распределенную по контуру, то потенциал будет падать по линейному закону по мере удаления от положительного электрода батареи (рис. 1). При превращении энергии электрического тока во внутреннюю проводник нагревается.

Рис.1
Дж. Джоулем и Э.Ленцем экспериментально было установлено, что количество тепла, выделяющегося в проводнике, определяется по формуле
Q = I2Rt, (10)
где I - сила тока в проводнике; R - сопротивление проводника; t -время: движения тока.
Зная закон Ома и закон Джоуля-Ленца, можно вывести закон Ома для неоднородного участка цепи, т.е. такого, в котором на заряды действуют как электростатические, так и сторонние силы.
Пусть дана неоднородная цепь (рис. 2).

Рис. 2
Согласно закону сохранения энергии количество тепла, выделенного в цени, равно сумме работы сил электрического поля и работы сторонних сил источника тока:
Q=Aэл.поля +Аст.поля ,
где Aэл.поля =q(φA-φB) - работа сил электростатического поля; Аст.сил =±qε - работа сторонних сил (положительная, см. рис. 2а; отрицательная, см. рис. 2,б).
Учитывая, что Q = I2(R + г)t,
где I - сила тока в цепи; R - сопротивление внешнего участка цепи (нагрузки); r - внутреннее сопротивление источника, получим следующее выражение:
I2(R + r)t = q(φA-φB)±qε.
Принимая во внимание, что I =  , последнее выражение можно записать так:
, последнее выражение можно записать так:
I(R + r)q = qφA -φB)±qε.
Сокращая на q, получим
I(R + r)=(φА- φB)±ε (11)
Выражение (11) представляет собой закон Ома для неоднородного участка цепи, где I(R+r) - падение напряжения на участке цепи UR+r; (φА- φB) – разность потенциалов, обозначаемая буквой U без индекса.
При использовании этого закона необходимо учитывать правило знаков: направление обхода участка цепи задает индексация потенциалов точек А и В.
Падение напряжения I(R+r) берется со знаком «плюс», если направление тока совпадает с направлением обхода участка цепи.
ЭДС источника е также берется со знаком «плюс», если напряженность поля сторонних сил совпадает с направлением обхода участка цепи.
Если цепь замкнута, т.е. φА = φв и φА – φв = 0, то
 (12)
(12)
Выражение (12) представляет собой закон Ома для замкнутой цепи: если сопротивление нагрузки равно нулю (R=0), то сила тока короткого замыкания рассчитывается по формуле
 (13)
(13)
Одним из самых удобных методов определения электродвижущих сил является компенсационный метод. Схема, отражающая его, изображена на рис. 3
(ε0 - вспомогательный источник тока с ЭДС, заведомо превосходящей ЭДС исследуемого источника и известную ЭДС εн нормального элемента).

Рис. 3
При помощи переключателя К мы можем подсоединить к цепи либо исследуемый источник, либо нормальный элемент. R, реохорд, - проволока с подвижным контактом, натянутая на линейку со шкалой (вместо проволоки может использоваться навитая на стержень спираль).
Включим в цепь исследуемый источник. Запишем закон Ома для неоднородного участка цепи:
IrR = (φс-φА)-εх, (14)
где Ir - ток, идущий по гальванометру; R - сопротивление всего неоднородного участка.
Перемещая контакт С по реохорду, мы изменим разность потенциалов φс-φА. Так как (φс-φА)>εх,то можно найти такое положение X, при котором
(φс - φА)=εх (15)
При этом условии Ir =0; правая часть равенства (14) обратится в нуль. Величина εх компенсируется разностью потенциалов φx-φА.
При смещении контакта С от X к А разность потенциалов (φB-φА) будет меньше εх, а ток также поменяет направление.
Замена исследуемого источника на нормальный элемент при помощи переключателя К компенсирует его ЭДС (благодаря перемещению контакта С в положение N). Должно выполняться условие
φN-φА=εх (16)
Обратить внимание на то, что компенсация ЭДС возможна только в том случае, если вспомогательный источник  и компенсируемые источники
и компенсируемые источники 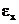 или
или  включены одноименными полюсами навстречу друг другу.
включены одноименными полюсами навстречу друг другу.
Разделим равенство (15) на (16):

Учитывая, что  и
и  =
=  , по закону Ома для однородных участков цепи ХА и NA
, по закону Ома для однородных участков цепи ХА и NA

где  - сопротивление на участке ХА; RN - сопротивление на участке NA.
- сопротивление на участке ХА; RN - сопротивление на участке NA.
Ток, идущий по реохорду, при этом одинаков. Сократив на I, получим
формулу:

Откуда 
Сопротивление участка прямо пропорционально его длине.
Следовательно, 

где  - длина участка АХ;
- длина участка АХ;  - длина участка AN.
- длина участка AN.
Окончательная формула имеет вид
 (17)
(17)
Сопротивление ro служит для изменения чувствительности микровольтметра и предохраняет его от высокого тока.
Порядок выполнения работы
1. Получить допуск у преподавателя. Включить установку.
2. С помощью ключа К1 подсоединить источник  .
.
3. Переключателем К к компенсационной цепи подсоединить источник 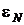 (значение
(значение 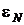 дано на стенде. Для сохранения стабильности элемента
дано на стенде. Для сохранения стабильности элемента  и
и 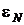 цепь включать на короткое время).
цепь включать на короткое время).
4. Перемещая свободный контакт по реохорду, добиться нулевого значения
силы тока в микроамперметре, т.е. тем самым, добиться полной компенсации значения 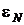 разностью потенциалов на реохорде R. Измерить расстояние
разностью потенциалов на реохорде R. Измерить расстояние  по линейке. Полученный результат занести в таблицу.
по линейке. Полученный результат занести в таблицу.
| i | 
| 
| 
| 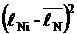
|
5. С помощью переключателя К подсоединить к компенсационной цепи
источник 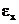 , см. рис. 3.
, см. рис. 3.
6. Перемещая свободный конец по реохорду, добиться нулевого значения силы тока в микроамперметре, т.е. тем самым добиться полной компенсации значений  разностью потенциалов на реостате R. Измерить расстояние
разностью потенциалов на реостате R. Измерить расстояние  на линейке. Полученный результат занести в таблицу.
на линейке. Полученный результат занести в таблицу.
7. Опыт повторит 5 раз.
8. Вычислить значение 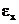 по формуле (17);
по формуле (17);

8. Найти ошибку в измерениях  и
и  по формулам
по формулам

 ;
;  .
.
9. Найти относительную ошибку измерений:

11.Определить доверительную границу измерений:

11.Ответ записать в виде
 ;
;  .
.
Контрольные вопросы
1.Что такое электрический ток, сила тока, плотность тока?
2. Вывести закон Ома для полной цепи.
3. Каков физический смысл ЭДС? Что такое сторонние силы? Каково их на
значение?
4 Чем компенсируется неизвестная ЭДС при достижении нулевого показания гальванометра?
ь. Если в схеме компенсации источник заменить другим источником с такой же ЭДС, но с большим внутренним сопротивлением, то в какую сторону следует сместить движок реохорда для восстановления компенсации?
ЛАБОРАТОРНАЯ РАБОТА № 3
ИССЛЕДОВАНИЕ ЗАКОНОВ ПОСТОЯННОГО ТОКА
Цель работы: исследование зависимости величины UR (падения напряжения на внешнем сопротивлении цепи) от величины силы тока; определение ЭДС и внутреннего сопротивления источника; изучение зависимости между Р, полной мощностью всей цепи; PR, мощностью внешней части цепи; Рr, мощностью внутри источника, КПД источника и внешним сопротивлением R.
Приборы и оборудование: установка для изучения законов постоянного тока.
Теоретические сведения
Работа по переносу электрического заряда определяется по формуле

Так как величина заряда q=It, то работа электрического тока на участке цепи
A = UIt.
Для однородного участка цепи U=IR, т.е.
A = I2Rt = 
Так как мощность  то P=IU; для однородного участка цепи
то P=IU; для однородного участка цепи
 (1)
(1)
где PR - мощность, выделяемая во внешней части цепи, обладающей сопротивлением R.
Учитывая закон Ома для замкнутой цепи

получим выражение
 . (2)
. (2)
Взяв производную  и приравняв ее к нулю, найдем, что PR будет иметь максимальное значение при R=r, т.е. когда внешнее сопротивление цепи равно внутреннему сопротивлению источника. В замкнутой цепи работу совершают только сторонние силы. По определению ЭДС
и приравняв ее к нулю, найдем, что PR будет иметь максимальное значение при R=r, т.е. когда внешнее сопротивление цепи равно внутреннему сопротивлению источника. В замкнутой цепи работу совершают только сторонние силы. По определению ЭДС
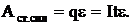
Полная мощность всей замкнутой цепи

Учитывая закон Ома для замкнутой цепи, получим выражение
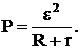 (3)
(3)
Коэффициент полезного действия источника тока рассчитывается по формуле
 (4)
(4)
Для исследования законов постоянного тока применяется установка, схема которой изображена на рис. 1  - источник тока; mA – миллиамперметр для измерения тока; V – вольтметр для измерения напряжения на внешнем резисторе;
- источник тока; mA – миллиамперметр для измерения тока; V – вольтметр для измерения напряжения на внешнем резисторе;  - магазин резисторов, при помощи которого можно устанавливать необходимое сопротивление).
- магазин резисторов, при помощи которого можно устанавливать необходимое сопротивление).
По закону Ома для замкнутой цепи
 (5)
(5)

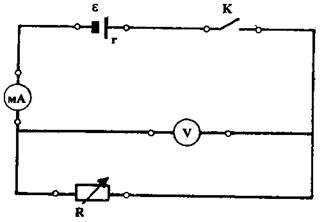
Рис. 1
График зависимости UR(I), см. рис. 2, есть прямая линия, отсекающая на оси UR значение, равное ЭДС источника ε, а на оси I-значение, равное силе тока короткого замыкания 
Внутреннее сопротивление источника –

Мощность внешней части цепи (полезная мощность) –
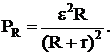

Рис. 2
Графиком зависимости PR(R), см. рис. Заявляется кривая линия, имеющая экстремальную точку при R=r и асимптотически приближающаяся к оси сопротивления R:
 →0 при R→0;
→0 при R→0;
 при R=0
при R=0
Полная мощность равна 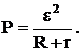
Графиком зависимости Р(R) является гипербола (рис. 4):
При R→0 
При R→∞ Р→0.
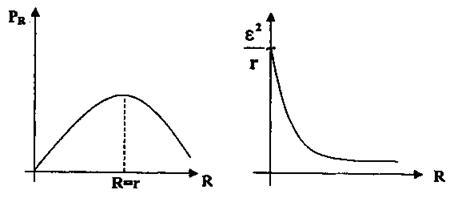
Рис. 3 Рис. 4
Коэффициент полезного действия источника тока 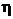 определяется по формуле (4)
определяется по формуле (4)

и имеет график, асимптотически приближающийся к горизонтальной прямой  ; при R→∞
; при R→∞ 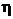 →1 (рис. 5).
→1 (рис. 5).
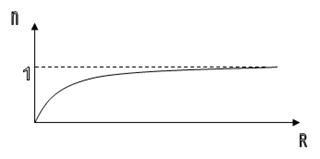
Рис.5
Порядок выполнения работы
1.Собрать рабочую схему (рис. 1) на тренаже и показать ее преподавателю.
2. Получив допуск, подойти к готовой установке и замкнуть цепь ключом К.
3. На магазине резисторов установить сопротивления R, равные 10, 20, 30 Ом
и т.д. Выбрать 30 точек, записывая при этом показания миллиамперметра и
вольтметра в таблицу.
Таблица
| R | I | 
| 
| 
| 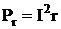
| 
|
4. По данным таблицы построить график зависимости  так, чтобы число
так, чтобы число
экстремальных точек, лежащих ниже и выше этой прямой, было одинаково.
Разброс точек происходит из-за случайных явлений, сопровождающих процесс измерения.
5. По графику определить ЭДС источника ε и внутреннее сопротивление г, учитывая, что  при I=0,
при I=0, 
6. Провести дополнительные измерения I и  при R=r и в окрестности этой
при R=r и в окрестности этой
точки через 2 Ома.
7. Заполнить нее графы таблицы по расчетным формулам, указанным в ней.
8. По данным таблицы построить графики зависимостей P(R), PR(Р), Pr(R)
9. По данным таблицы построить графики зависимости 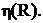
10.Сравнить полученные экспериментальные кривые с теоретическими
кривыми.
Контрольные вопросы
1.Дать понятие мощности тока и назвать единицы ее измерения.
2. Какие виды мощности вы знаете? Дать их краткую характеристику.
3. От чего зависит КПД источника тока?
4. По графику (рис. 6) определить зависимость UR(I), ЭДС источника  , силу
, силу
тока короткого замыкания  ; внутреннее сопротивление источника г, силу
; внутреннее сопротивление источника г, силу
тока и падение напряжения, при которых мощность, выделяемая на внешнем
резисторе, будет максимальной.

Рис. 6
5. На координатной плоскости изображены 3 графика (рис. 7). Указать, какой из них соответствует графикам зависимости: Pr(R) - полезной мощности от внешнего сопротивления, P(R) - полной мощности от внешнего сопротивления, 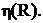 КПД источника от внешнего сопротивления.
КПД источника от внешнего сопротивления.

Рис. 7
Определить по этим графикам ЭДС источника ε, внутреннее сопротивление источника r и записать аналитическое выражение зависимостей P(R), PR(R), 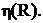
6. Как изменятся графики зависимостей PR(R), UR(I), PR(I), если внутреннее сопротивление источника увеличится вдвое? Почему лампочка в 3,5 В не горит при подключении ее к батарее «Крона» - источнику питания для транзисторных приемников (ЭДС источника равна 9В)?
ЛАБОРАТОРНАЯ РАБОТА 4
ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА С ПОМОЩЬЮ
ЭЛЕКТРОННОГО ВОЛЬТМЕТРА
Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов.
Приборы и оборудование: источник питания ( ), электронный вольтметр (В7-16А), потенциометр (R14), эталонный конденсатор (Сэт), исследуемый конденсатор (Сх), переключатель (S4).
), электронный вольтметр (В7-16А), потенциометр (R14), эталонный конденсатор (Сэт), исследуемый конденсатор (Сх), переключатель (S4).
Теоретические сведения
Опытным путем было установлено, что в природе существует два типа электрических зарядов, условно названных положительными и отрицательными. Одноименные заряды отталкиваются друг от друга, разноименные притягиваются.
Р, Милликеи доказал, что электрический заряд дискретен, т.е. величина заряда любого тела составляет целое число, кратное элементарному электрическому заряду е (e=1,6∙10-19 Кл). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
В результате обобщения опытных данных был сформулирован фундаментальный закон природы - закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри нее.
Единица электрического заряда, 1 кулон (Кл), - это электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за время, рапное 1с:
1Кл=1 А∙1с.
Закон взаимодействия неподвижных точечных электрических зарядов был открыт Кулоном: сила взаимодействия F двух точечных зарядов прямо пропорциональна величине зарядов q1 и q2 и обратно пропорциональна квадрату расстояния г между ними:
 ∙
∙  (1)
(1)
где  - электрическая постоянная;
- электрическая постоянная;  - диэлектрическая проницаемость среды (безразмерная величина).
- диэлектрическая проницаемость среды (безразмерная величина).
Напряженность  электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:
электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:

Направление вектора  совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряженности электрического поля:
совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряженности электрического поля:

Графически электростатическое поле изображают с помощью линий напряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженности (рис. I).
Величина

называется потоком вектора напряженности через площадку dS. Здесь dS = dSn - вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке ( ).
).
Электростатические поля подчиняются принципу суперпозиции: напряженность  результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:
результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:
 (3)
(3)
где  - напряженность электростатического поля, созданного i-м зарядом.
- напряженность электростатического поля, созданного i-м зарядом.

Рис. 1
Теорема Остроградского-Гаусса для электростатического поля в вакууме звучит так: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на eq:
 (4)
(4)
Из теоремы Гаусса следует, что напряженность электростатического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями в вакууме будет равна
 , (5)
, (5)
где  - поверхностная плотность заряда плоскостей.
- поверхностная плотность заряда плоскостей.
Если между заряженными плоскостями находится изолятор с диэлектрической проницаемостью  , то напряженность поля внутри него уменьшается в
, то напряженность поля внутри него уменьшается в  раз (рис. 2):
раз (рис. 2):
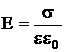 (6)
(6)
Электростатическое поле является полем консервативных сил, т.е. работа, совершаемая силами поля по перемещению электрического заряда из одной точки пространства в другую, не зависит от траектории движения заряда, а определяется только его начальным и конечным положениями. Для такого рода полей можно ввести понятие потенциальной энергии заряда, численно равной работе, совершаемой силами электростатического поля по перемещению его ич данной точки пространства в другую (ту, в которой потенциальная энергия заряда равна нулю).

Рис. 2
Как правило, потенциальная энергия заряда, удаленного в бесконечность, считается равной нулю. Поэтому она будет равна
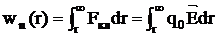 , (7)
, (7)
где  - модуль радиус-вектора
- модуль радиус-вектора 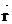 ;
;  - кулоновская сила;
- кулоновская сила;  - напряженность электростатического поля; qo - электрический заряд.
- напряженность электростатического поля; qo - электрический заряд.
Если заряд q0 перемещается из первой точки во вторую(определяются соответственно радиус-векторами  и
и 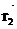 то работу, совершаемую силами поля, можно найти как разность работ
то работу, совершаемую силами поля, можно найти как разность работ

A 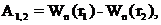 (8)
(8)
где  и
и  ;
;  и
и  - работы, совершаемые силами поля при перемещении заряда из первой и второй точек в бесконечность.
- работы, совершаемые силами поля при перемещении заряда из первой и второй точек в бесконечность.
Потенциал - физическая величина, определяемая работой сил поля по перемещению единичного положительного заряда из данной точки в бесконечность:

Единица потенциала - вольт (В): 1 В - потенциал такой точки поля, в которой заряд в 1Кл обладает потенциальной энергией в 1 Дж:

Поскольку  , то
, то

 (10)
(10)
Отсюда

 (11)
(11)
Зная потенциал в каждой точке пространства  можно найти напряженность электростатического поля:
можно найти напряженность электростатического поля:
 (12)
(12)
Знак «минус» указывает на то, что вектор напряженности Ё направлен в сторону убывания потенциала.
Потенциал уединенного проводника прямо пропорционален его заряду;

При этом величину  (13)
(13)
называют электроемкостью уединенного проводника. Единица электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1Кл, т.е.

Для накопления значительных зарядов служат конденсаторы, состоящие из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы подразделяются на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению накопленного заряда q к разности потенциалов  между обкладками:
между обкладками:

где  напряжение между обкладками. Плоский конденсатор обладает емкостью
напряжение между обкладками. Плоский конденсатор обладает емкостью

где  - диэлектрическая проницаемость изолятора;
- диэлектрическая проницаемость изолятора;  - электрическая постоянная; S - площадь обкладки; d - расстояние между обкладками.
- электрическая постоянная; S - площадь обкладки; d - расстояние между обкладками.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи параллельно или последовательно. У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна  см рис. 3.
см рис. 3.

Если емкости отдельных конденсаторов  то их заряды равны соответственно
то их заряды равны соответственно

а заряд батареи конденсаторов-

Полная емкость батареи –
 , (16)
, (16)
т.е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи, см. рис. 4, равна
 .
.
Причем для любого из рассматриваемых конденсаторов
 .
.

С другой стороны,

откуда  , (17)
, (17)
т.е. при последовательном соединении конденсаторов суммируются обратные величины емкостей.
Если дана емкость эталонного конденсатора Сэт, то неизвестную емкость другого конденсатора Сх можно определить следующим образом.
Сначала конденсатор Сэт зарядить от источника постоянного тока (рис.5а). При этом накапливается заряд q. С помощью вольтметра измерить напряжение на обкладках конденсатора:

Тогда
 .
.
Отсюда
 . (18)
. (18)
Затем эталонный конденсатор отключить от источника питания и к нему параллельно присоединить конденсатор неизвестной емкости Сх (рис. 5б). Электрический заряд q распределится по конденсаторам Сэт и Сх.

Согласно закону сохранения зарядов в замкнутой системе
 (19)
(19)
где q1, q2- электрические заряды на конденсаторах Сэти Сх.
После этого измерить напряжение  на обкладках конденсаторов, причем
на обкладках конденсаторов, причем
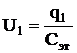 и
и  .
.
Отсюда
 и
и  . (20)
. (20)
Поэтому

В результате  (21)
(21)
Порядок выполнения работы
1. Тумблером включить установку.
2. Клеммы Сэт проводниками соединить с клеммами переключателя S2.
3. Переключателем S включить напряжение от источника питания на эталонном конденсаторе.
4. Установить движком потенциометра R на напряжение U0=(1±0,2) В. Снять показания вольтметра.
5. Переключателем S2 отключить эталонный конденсатор от источника питания.
6. Соединить проводниками Сэт и Сх1 параллельно и снять показания вольтметра U1.
7. Тумблером S3 разрядить конденсаторы.
8. Подавая на эталонный конденсатор напряжение от 1 В до 1,4 В, провести измерения 3 раза. Данные занести в таблицу.
9. Для каждой пары значений напряжений U0 и U1 найти электроемкость по формуле
 .
.
Затем определить среднюю величину электроемкости Сх1(ср). Результаты вычислений занести в таблицу.
10. По п.п. 3-9 найти электроемкость Сх2.
Таблица
| U0 | U1 | Cx1 | U0 | U2 | Cx2 | U0 | Uпар | Cпар | U0 | Uпосл | Cпосл |

| 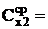
| 
| 
|
11. Соединить конденсаторы Сх1 и Сх2 параллельно.
12. По п.п. 3-9 найти электроемкость батареи Спар.
13. Соединить конденсаторы Сх1 и Сх2 последов