Каким знаком обозначается принадлежность?
а) Z б) ∈ в) = г) N
8). Какое значение имеет x в уравнении cos x = −1?
а) π + 2πn, n ∈ ℤ б) 
− πn, n ∈ ℤ в) 2π + 
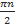, n ∈ ℤ г) π − πn, n ∈ ℤ
9). Чему равен результат выражения sin2x − 1 + cos2x после упрощения?
а) 
б) 1 в) cos2x г) 0
10). Решите уравнение tg x = 1
а) x = 
- 2πn, n ∈ ℤ б) x = -3π + πn, n ∈ ℤ в) x = 
+ πn, n ∈ ℤ г) x = 2πn, n ∈ ℤ
Чему равен arcctg(-1)?
а)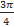 
б) в) − г) 0
При каких значениях x можно использовать выражение arcsin x?
а) −1 ⩾ x ⩾ 1 б) −1 ⩽ x ⩽ 1 в) 0 > x > 1 г) −1 < x > 1
Какое уравнение не имеет корней?
а) sin x = 0 б) cos x = − 
в) sin6x = 0,6 г) sin x = 
Тригонометрические уравнения.
2 вариант
1). Какое решение имеет тригонометрическое уравнение cos(x) = a, если |a| ⩽ 1?
a) x = (-1)n arcsin(a) + πn б) x = ±arccos(a) + 2πn
в) x = arcsin(a)n + πn г) x = 2πn
2). Решите уравнение tg5x =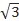 
а) x = 5πn, n ∈ ℤ б) x =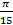 
+ 
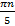, n ∈ ℤ
в) x = 
- πn, n ∈ ℤ г) x = -π + 
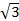πn, n ∈ ℤ
3). Что является целым числом в x = 2πn?
а) n б) 2 в) π г) x
4). Какой способ решения как основной можно применить для уравнения:
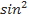x + 2 sin x − 3 = 0?
а) способ разложения на множители
б) способ однородных уравнений
в) способ с применением ограниченности суммы
г) способ замены переменной
5). Для какого выражения подходит область значений (− 
; )?
а) 3arctg(-x) б) arcsin x в) arctg x г) 
arccos x
6). Чему равен cos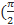 
+ 2πn) = …
а) 1 б) 0 в) -2 г) 7
Каким знаком обозначается множество целых чисел?
а) Z б) ∈ в) = г) N
8). Какое значение имеет x в уравнении cos x = 1?
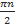а) π + 2πn, n ∈ ℤ б) − πn, n ∈ ℤ в) 2π + , n ∈ ℤ г) 2πn, n ∈ ℤ
9). Чему равен результат выражения sin2x − 2 + cos2x после упрощения?
|
|
а) 0 б) 1 в) −1 г) cos2x
10). Решите уравнение tg x = 0
а) x = − 2πn, n ∈ ℤ б) x = πn, n ∈ ℤ в) x = + πn, n ∈ ℤ г) x = 2πn, n ∈ ℤ
11). Чему равен arccos(−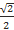 
)?
а) 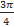б) в) − г) 0
При каких значениях x можно использовать выражение arccos x?
а) −1 ⩾ x ⩾ 1 б)) −1 < x > 1 в) 0 > x > 1 г) −1 ⩽ x ⩽ 1
Какое уравнение не имеет корней?
а) sin x = 0 б) cos x = − в) sin6x = 1,6 г) sin x = 
Практическая работа №9
Правила дифференцирования, ее геометрический и механический смысл.
1 вариант Канноев
2 вариант Мелкозеров, Тренин, Холманский, Шошин, Эльжуркаев.
1 вариант https://docs.google.com/forms/d/1D4X0p1GCS5wIcRVlWE0a92i-8IwIpX7ztzWXakh3IVw/edit
2 вариант https://docs.google.com/forms/d/1DFg434xs-Uy3Aujm-3C_-rXkqf8cCQ1XJuPVM2y4Kkg/edit
Самостоятельная работа по теме: Производная показательной и логарифмической функций.
1 вариант Александров, Дубовенко, Елагина, Елизаров, Жорова, Костюк, Лахтачев
2 вариант Ломаев, Лутохин, Мелкозеров, Осипов, Тренин, Тырков, Холманский, Шошин, Эльжуркаев.
1 вариант
Основная ссылка:
https://onlinetestpad.com/3twprliwmgiq2
2 вариант
Основная ссылка:
https://onlinetestpad.com/cb6nnxhwrwjsw
Практическая работа №10
Применение производной функции.
1 вариант Александров, Алексеенко, Бобин, Дубовенко, Елагина, Ивков, Канноев, Костюк.
2 вариант Мамонова, Мелкозеров, Сергеев, Холманский, Шошин, Эльжуркаев.
1 вариант
https://docs.google.com/forms/d/1b1MrRHlXgSRpgW9V7VADUPjQkOKTzDr78GaEg407UPg/edit
2 вариант
https://docs.google.com/forms/d/1duiA53xRRLiiQvjV46xVUAvmE3LqytkMCsEbwnXl3Co/edit
Практическая работа.
«Вычисление площади криволинейной трапеции».
1 вариант Канноев, Сергеев, Шошин
|
|
2 вариант Дубовенко, Мамонова, Осипов, Эльжуркаев.
3 вариант Елизаров, Тырков
4 вариант Ивков, Мелкозеров, Холманский
1 вариант
1) Вычислите (предварительно сделав рисунок) двумя способами площадь фигуры, ограниченной указанными линиями:
у = 4х – 8, у = 0, х = 4.
2) Найдите площадь фигуры, ограниченной графиком функции
f(x) = x2 + 5x + 6, прямыми x = −1, x = 2 и осью абсцисс.
3) Вычислить площадь криволинейной трапеции, ограниченной графиком функции
у = х3 – х, у = 0, х = −1, х = 2.
2 вариант
1) Вычислите (предварительно сделав рисунок) двумя способами площадь фигуры, ограниченной указанными линиями:
у = 3х + 6, у = 0, х = 1.
2) Найдите площадь фигуры, ограниченной графиком функции
f(x) = x2 − 6x + 8, прямыми x = −2, x = −1 и осью абсцисс.
3) Вычислить площадь криволинейной трапеции, ограниченной графиком функции
у = х3 – 4х, у = 0, х = −2, х = 1.
3 вариант
1) Вычислите (предварительно сделав рисунок) двумя способами площадь фигуры, ограниченной указанными линиями:
у = 5х – 10, у = 0, х = 4.
2) Найдите площадь фигуры, ограниченной осями координат, графиком функции
f(x) = x2 − 6x + 9 и прямой x = 2.
3) Вычислить площадь криволинейной трапеции, ограниченной графиком функции
у = 
х3, у = 0, х = −1, х = 2.
4 вариант
1) Вычислите (предварительно сделав рисунок) двумя способами площадь фигуры, ограниченной указанными линиями:
у = 2х + 4, у = 0, х = 1.
2) Найдите площадь фигуры, ограниченной осями координат, графиком функции
f(x) = x2 + 6x + 16 и прямой x = −2.
3) Вычислить площадь криволинейной трапеции, ограниченной графиком функции
|
|
у = 1 − х3, у = 0, х = −2, х = −1.
Математический диктант «Параллельность прямых и плоскостей»
1 вариант Александров, Алексеенко, Бобин, Григорчук, Елизаров. Ивков, Канноев, Ломаев, Лутохин
2 вариант Мамонова, Осипов, Пигульский, Столповских, Тренин, Шошин, Эльжуркаев
1 вариант Основная ссылка:
https://onlinetestpad.com/cgg4jar5imjwo
2 вариант
Основная ссылка:
https://onlinetestpad.com/3mjdkedjfzjzi
Математический диктант «Перпендикулярность прямых и плоскостей»
1 вариант Григорчук, Елизарова, Зайцев, Костюк, Лахтачев, Лутохин, Пигульский, Мамонова
2 вариант Канноев, Лутохин, Столповских, Тренин, Шошин, Эльжуркаев
1 вариант
Основная ссылка:
https://onlinetestpad.com/sehvqsifbpatg
2 вариант
Основная ссылка:
https://onlinetestpad.com/hdk3idiv6zhxm