Деревянные конструкции
Расчет элементов ДК по предельным состояниям. Расчет на смятие. Расчет элементов ДК по предельным состояниям. Расчет на скалывание.
В соответствии с действующими в России нормами деревянные конструкции должны рассчитываться по методу предельных состояний.
Предельными являются такие состояния конструкций, при которых они перестают удовлетворять требованиям эксплуатации. Внешней причиной, которая приводит к предельному состоянию является силовое воздействие (внешние нагрузки, реактивные силы). Предельные состояния могут наступать под влиянием условий работы деревянных конструкций, а также качества, размеров и свойств материалов. Различают две группы предельных состояний:
1 – по несущей способности (прочности, устойчивости).
2 – по деформациям (прогибам, перемещениям).
^ Первая группа предельных состояний характеризуется потерей несущей способности и полной непригодностью к дальнейшей эксплуатации. Является наиболее ответственной. В деревянных конструкциях могут возникать следующие предельные состояния первой группы: разрушение, потеря устойчивости, опрокидывание, недопустимая ползучесть. Эти предельные состояния не наступают, если выполняются условия:
σ ≤ R,
τ ≤ Rск (или Rср),
т.е. когда нормальные напряжения (σ) и касательные напряжения (τ) не превышают некоторой предельной величины R, называемой расчетным сопротивлением.
Расчет на изгиб (прочность, устойчивость, жесткость, косой изгиб). Как определить требуемое количество гвоздей в соединении.
Изгибаемые элементы
В изгибаемых элементах от нагрузок, действующих поперек продольной оси, возникают изгибающие моменты ^ М и поперечные силы Q,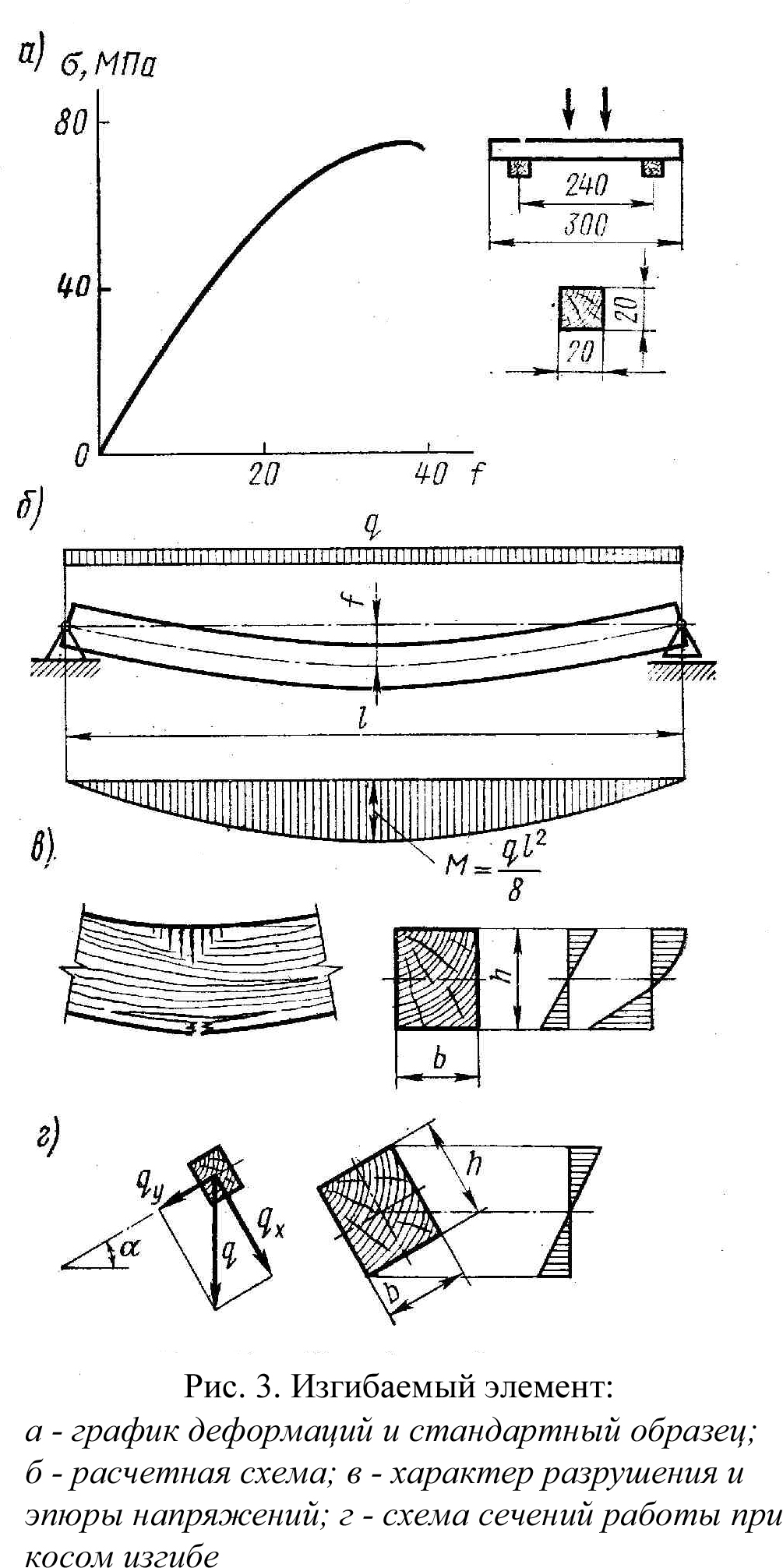 
определяемые методами строительной механики. Например, в однопролетной балке пролетом l от равномерно-распределенной нагрузки q возникают изгибающие моменты 
|
|
и поперечные силы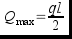 
.
От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба σ, которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается.
Диаграмма как и для сжатия, примерно до половины, имеет линейное очертание, затем изгибается, показывая ускоренный рост прогибов.
=80 МПа – предел прочности чистой древесины на изгиб при кратковременных испытаниях. Разрушение образца начинается с появления складок в крайних сжатых волокнах и завершается разрывом крайних растянутых. Расчетное сопротивление изгибу по СНиП II-25-80 рекомендуется принимать таким же, как и при сжатии, т.е. для 1 сорта Rи =14 МПа – для элементов прямоугольного сечения высотой до 50 см. Брусья с размерами сечения 11 – 13 см. при высоте сечения 11 – 50 см. имеют меньше перерезанных волокон при распиловке, чем доски, поэтому их прочность повышается до Rи =15 МПа. Бревна шириной свыше13 см. при высоте сечения 13 – 50 см. совсем не имеют перерезанных волокон, поэтому Rи =16 МПа.
Расчет изгибаемых элементов на прочность
Производится по формуле:
σ= 
, где
М – максимальный изгибающий момент,
Wрасч – расчетный момент сопротивления поперечного сечения.
Для наиболее распространенного прямоугольного сечения
; 
.
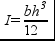Подбор сечения изгибаемых элементов производится по этой же формуле, определяя 
, затем, задавая
|
|
один из размеров сечения (b или h), находят другой размер.
2. Расчет на устойчивость поской формы дефорирования элементов прямоугольного постоянного сечения
Производят по формуле:
σ= 
, где
М – максимальный изгибающий момент на рассматриваемом участке lp,
Wбр – максимальный момент сопротивления брутто на рассматриваемом участке lp, φм – коэффициент устойчивости.
Коэффициент φм для изгибаемых элементов прямоугольного постоянного поперечного сечения шарнирно-закрепленных от смещения из плоскости изгиба, следует определять по формуле:
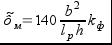,где
lp – расстояние между опорными сечениями элемента (расстояние между точками закрепления сжатого пояса),
b – ширина поперечного сечения,
h – максимальная высота поперечного сечения на участке lp,
kф – коэффициент, зависящий от формы эпюры на участке lp (определяется по таблице СНиП II-25-80).
При расчете элементов переменной высоты сечения значение коэффициента φм следует умножать на коэффициент kжм, а при подкреплении из плоскости изгиба в промежуточных точках растянутой кромки – на коэффициент kпм.
Оба эти коэффициента определяются по СНиП.
При наличии точек закрепления растянутых зон n≥ 4, kжм =1.
Проверку устойчивости плоской формы изгиба элементов постоянного двутаврового или коробчатого сечения следует производить в тех случаях, когда lp≥ 7 b, где b – ширина сжатого пояса поперечного сечения. Расчет следует производить по формуле:
, где
φ – коэффициент продольного изгиба сжатого пояса,
Rc – расчетное сопротивление сжатию,
Wбр – момент сопротивления брутто, в случае фанерных стенок – приведенный момент сопротивления в плоскости
|
|
изгиба элемента.