Пункт 3: Построение годографа разомкнутой ИСАУ
Построим годограф разомкнутой ИСАУ по выражению W*(p):
|
Построим годограф по точкам. Для этого воспользуемся формулу Эйлера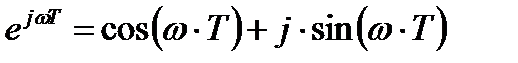 
. Домножив полученное выражение на комплексно-сопряженное знаменателю число получим:
|
Выделим действительную и мнимую часть выражения, получим соответственные результаты:
| w | Координаты точек |
| w0/10 | 5.422-38.337j |
| 2w0/10 | -1.521-10.021j |
| 3w0/10 | -1.865-5.58j |
| 4w0/10 | -1.95-3.731j |
| 5w0/10 | -1.984-2.682j |
| 6w0/10 | -2-1.98j |
| 7w0/10 | -2.009-1.458j |
| 8w0/10 | -2.014-1.038 |
| 9w0/10 | -2.017-0.678 |
| w0 | -2.019 |
Построим АФХ по точкам:
|
Как можно видеть, АФХ, построенный по точкам, совпадает с построенным ранее.
Также возможно построение годографа ИСАУ по годографу 
. Для этого необходимо воспользоваться формулой
, где w0=2* 
Стоит отметить, что эта формула позволяет построить лишь приближенно.
Годограф, построенный данным образом для данной системы, будет выглядеть так:
|
Пункт 4: Оценка устойчивости замкнутой импульсной САУ и нахождение предельного коэффициента усиления
а) По критерию Найквиста:
Годограф 
охватывает точку (-1;j0), то есть рассматриваемая САУ в замкнутом состоянии является неустойчивой.
Рассчитаем Кпред. При К=0.727 годограф разомкнутой системы охватывает точку (-1;j0), по критерию Найквиста система является неустойчивой, необходимо уменьшать значение К.
Составим пропорцию:
К - 2.019
Кпред -1
Получим Кпред=0.36
б) По критерию Гурвица
Найдем передаточную функцию замкнутой ИСАУ:
W*з(p)= 
Рассмотрим знаменатель полученного выражения. Проведем замену 
В свою очередь, z заменим на 
и приравняем полученное выражение к нулю.
Приведем левую часть уравнения к общему знаменателю:
Чтобы система была устойчивой, должны выполняться следующие условия:
-Все коэффициенты при v и определитель Гурвица второго порядка положительные.
|
Система неустойчива. Найдем Кпр из уравнения 3:
|
в) Определение устойчивости САУ по корням характеристического уравнения:
Найдем корни характеристического уравнения:
Корни уравнения:
x 1 = -3.018
x 2 = 1.002
x 3 = 0.985
Видно, что есть корни уравнения по модулю больше единицы, то есть система неустойчива. Подставив в уравнение Кгр, найденное в предыдущих исследованиях, получим следующие корни:
x 1 = -1
x 2 = 0.005 + i × (-1)
x 3 = 0.005 - i × (-1)
То есть при данном К система находится на границе устойчивости.
Пункт 5: Построение переходного процесса для замкнутой ИСАУ
В предыдущем пункте была получена передаточная функция замкнутой ИСАУ. Подставив в нее числовые значения коэффициентов, получим:
|
Так как ИСАУ неустойчива, необходимо сделать коэффициент усиления в 1.75 раз меньше предельного, то есть k=0,2
|
Разделим это выражение на 
и перейдем от изображения к оригиналу:
Построим график переходного процесса:
|
Пункт 6: Определение статической и кинетической ошибки замкнутой импульсной САУ
Для расчета ошибок используются следующие формулы:
Тогда для статической ошибки:
На входе системы X(t)=1(t), то есть
|
Для кинетической ошибки
На входе системы X(t)=t×1(t), тогда
|
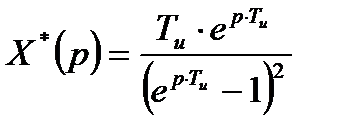
Национальный Исследовательский Университет
Московский Энергетический институт
Кафедра Управления и информатики
Расчетное задание по теме
«АНАЛИЗ ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
Вариант №74
| Выполнил | |
| Рубан С.В. | |
| Группа | А-2-08 |
| Принял | |
| Преподаватель | Коломейцева М.Б. |
Москва.2011г.