Определение мощности на привод водокольцевого вакуумного насоса

Потребная производительность вакуумного насоса определяется количеством доильных аппаратов. Общее их число составляет 24 штуки. Один доильный аппарат потребляет 5 м³/ч воздуха. Тогда потребная производи-тельность насоса составит 120 м³/ч.

Мощность определяем по формуле

, кВт (3.1) (6,1)

где − давление всасывания, (0,05 МН/м²);

− давление нагнетания, (0,15 МН/м²);

− производительность по всасыванию;

=0,6 изотермический коэффициент

Из данной формулы получаем = 7,5 кВт.

Принимаем электродвигатель с мощностью 7,5 кВт и частотой вращения 1440 об/мин. Двигатель АИР 132S4 ТУ-525.564-84 с диаметром вала 30 мм.

Определение радиуса ротора

Радиус ротора определяем по теоретической производительности вакуумного насоса

, м³/об (3.2) (7.3) (6.2)

где − радиус ротора, м

− эксцентриситет, м (составляет 1/8 )

− длина ротора, м

Тогда

(3.3) (6.3)

Откуда

(3.4) (7.4) (6.4)

С учетом числа оборотов вала насоса ( оборотов в минуту) получим

м.

Расчет вала

На валу закреплены муфта 1 и колесо 2 (рис. 4.4, а). Мощность, передаваемая электродвигателем N =7,5 кВт. Число оборотов электродвигателя n =1440 об/мин. Муфта передает вращающий момент

(3.5)

Длина вала между опорами l =500 мм; диаметр колеса D =200 мм. Определим диаметр вала по теории наибольших касательных напряжений.

Материал вала – сталь 45. Допускаемое напряжение принять [s] = 50 Н/мм².

Следует отметить, что муфта передает валу только вращающий момент, т. е. скручивает вал, но не изгибает его (собственный вес муфты и вала не учитывается, влияние их веса обычно невелико).

Таким образом, участок вала от муфты до колеса скручивается постоянным моментом М _К=49,74 Н×м. Сила F_t приложенная к ободу колеса, должна быть приведена к точке, лежащей на оси вала.

1. На рис. 4.4, б показана расчётная схема вала. При переносе силы F_t добавляется пара сил c моментом (сила этой пары отмечена на схеме двумя чертежами).

Плоскость действия пары сил перпендикулярна оси вала, и вал вращается с постоянной угловой скоростью, следовательно, = .

Отсюда

(3.6)

2.Расчетная схема вала при кручении изображена на рис. 4.4, в.

Пользуясь методом сечений, можно легко определить, что крутящий момент M _к= =49,74 Н×м возникает только на участке вала от муфты до колеса. Эпюра крутящих моментов изображена на рис. 4.4, .

3. Расчетную схему вала изображаем как балку на двух опорах с нагрузкой посередине (рис. 4.4, ), причем сила F_t будет направлена перпендикулярно оси.

Строим эпюру изгибающих моментов. Так как нагрузка приложена симметрично опор, реакция опор равна F_t /2=0,497/2=0,2487 кН и направлена вертикально вверх.

К балке приложены только сосредоточенные силы, следователь­но, эпюра изгибающих моментов очерчена наклонными прямыми ли­ниями. Для построе­ния эпюры достаточно вычислить изгибающие моменты в трех сечениях (A, B, C):

M _{И А} =0;

M _{И C} =0;

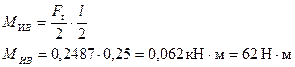(3.7)

Нужно обратить внимание, что при определении изгибающего момента в сечении В отбрасывается пра­вая или левая часть балки вместе с силой F_t, действие которой учитывается возникающей опорной реакцией F_t /2. На рис. 4.4, е показана эпюра изгибающих моментов.

4. Вычисляем по теории набольших касательных напряжений максимальный эквивалентный момент М _экв. Максимальный изгибающий М _{И max} и крутящий М _к: моменты возникают в сечении В, для которого вычисляем эквивалентный момент:

(3.8)

5. Определяем теперь диаметр вала

(3.9)

Окончательно принимаем d =32 мм.

Рис.4.4 Схема нагрузок и эпюры моментов вала