Как уже было показано, в качестве оптимальной структуры релейного регулятора может быть использована структура, обоснованная в п.6 (рис. 6.4).
Рисунок 7.1 – Схема релейного регулятора
В качестве численных значений изменяемых параметров структуры – значение коэффициентов и постоянной времени апериодического звена первого порядка. По умолчанию значение параметров:
1) Вектор коэффициентов – 1;
2) Вектор постоянных времени Т, с – 1;
При таких значениях график процесса, протекающего в системе будет выглядеть следующим образом:
Рисунок 7.2 – График процесса, протекающего в системе
Фазовый портрет процессов представлен на рисунке 7.3
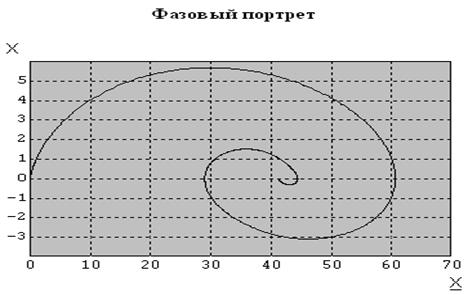
Рисунок 7.3 – Фазовый портрет процессов, протекающих в системе
На рисунке 7.2 видно,что присутствие обратной связи с апериодическим звеном 1-го порядка выводит систему из колебательного состояния, т.е. обратная связь останавливает реле до того как оно вошло в зону чувствительности.
Рисунок 7.3 представляет собой фазовый портрет системы.
Анализ графика (рис.6.2) даёт следующие результаты:
хуст=40 B, 
=±3,5 B.
tн= 69.43 c. Достигается при t = хуст.
xmax = 61.1311 B. Достигается при t = 18.6964 c
%
Составим передаточную функцию замкнутой обратной связи:
Необходимо согласовать какое постоянное время необходимо поставить. Для этого решим уравнение, представленное формулой (3), из которого можно вычислить постоянное время (T).
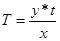, где (3)
y – выходной сигнал,
x – входной сигнал,
t – время за которое входной сигнал доходит до 70 В.
Так как входной сигнал равен 70В, выходной сигнал равен 40, время за которое входной сигнал доходит до 70В равно 3 секунды (время берется из рисунка 7.4)
|
|
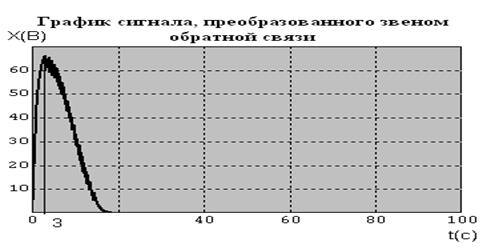
Рисунок 7.4 – График сигнала, преобразованного звеном обратной связи.
Подставим значение в (3):
с.
Подставим в апериодическое звено постоянное время равное 1,7 секунды. Посмотрим поведения переходного процесса при таких параметрах:
1.
1) Вектор коэффициентов – 1;
2) Вектор постоянных времени Т, с – 1,7;
Рисунок 7.5 – График процесса, протекающего в системе
Рисунок 7.6 – Фазовый портрет процессов, протекающих в системе
В переходном режиме качество системы не удовлетворяет требованиям, следовательно, чтоб в замкнутой системе регулирования имели место плавные (без перерегулирования) и быстрые переходные процессы необходимо увеличить коэффициент усиления звена, что понизит колебательный процесс.
2.
1) Вектор коэффициентов – 2;
2) Вектор постоянных времени Т, с – 1,7;
При таких значениях график процесса, протекающего в системе будет выглядеть следующим образом:
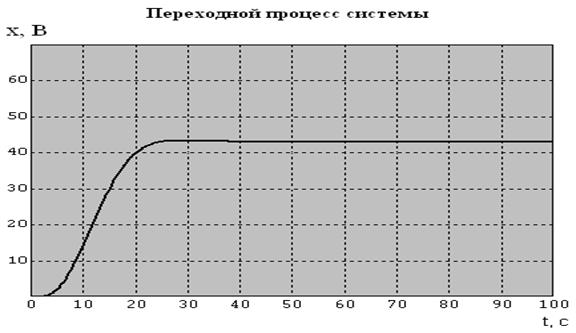
Рисунок 7.8 – График процесса, протекающего в системе
Фазовый портрет процессов представлен на рисунке 7.9
Рисунок 7.9 – Фазовый портрет процессов, протекающих в системе
Анализ графика (рис.7.8) даёт следующие результаты:
хуст=40 B, =±3,5 B.
tн= 20.55 с. Достигается при t = хуст.
xmax = 41.09 B. Достигается при t = 27.65 c
%, что находится в рамках допустимого.
Таким образом была выбрана структура и численные значения параметров для обеспечения в замкнутой системе регулирования плавных (без перерегулирования) и быстрых переходных процессов, ошибка регулирования не превышает 3.5 В.
Таким образом была выбрана структура и численные значения параметров для обеспечения в замкнутой системе регулирования плавных (без перерегулирования) и быстрых переходных процессов, ошибка регулирования не превышает 3.5 В. Параметры указаны в Таблице 2.
|
|
Таблица 2 – Подобранные параметры для звена обратной связи
| Коэффициент усиления | |
| Постоянная времени | 1.7 |
| Вектор начальных условий |
ВЫВОДЫ
В процессе написания курсовой работы был проведён анализ динамических свойств отдельно объекта управления и системы управления в целом, данных в задании, при помощи программы ПК «МВТУ», позволяющей вести расчёты в системах управления, сконструированных непосредственно в программе.
На базе данной системы управления был сконструирован релейный регулятор, к которому были подобраны параметры, отвечающие требованиям задания, что позволило понять на практике каким образом действуют релейные регуляторы и осуществляется переходной процесс в системе управления.
ЛИТЕРАТУРА
1. Бесекерский В.А.Теория систем автоматического регулирования.1975;
2. Попов Е.П. Теория линейных систем автоматического регулирования и управления.1989