Методы и модели решения задач оптимизации
Транспортных процессов
Сетевая модель комплекса работ в транспортировке. Среди инструментовоптимизации логистических процессов в транспортировке выделяется метод сете-вого планирования, это объясняется графической интерпретацией реальных путей транспортировки в виде сетей, а также необходимостью соблюдения определенной последовательности проведения работ по текущему ремонту и техническому об-служивания. В транспортировке задачи рационального планирования сложного комплекса работ имеют следующие общие черты:
весь комплекс работ представляет собой совокупность элементарных работ;
работы не могут выполняться в произвольном порядке, для начала одних работ требуется предварительное выполнение некоторых других.
Решение этих задач методами сетевого планирования предполагает по-строение сетевой модели комплекса работ. Сетевая модель изображается в виде сетевого графика, отображающего технологическую взаимосвязь между рабо-тами. В сетевом планировании основные элементы сетевого графика (дуги и вершины) принято называть работами и событиями.
Термин «работа» может иметь различные значения:
– действительная работа, требующая затрат времени и ресурсов;
– ожидание — процесс, не требующий затрат труда, но занимающий время (например, процессы сушки пиломатериалов, твердения бетона и т. д.);
– фиктивная работа — логическая связь между двумя или несколькими рабо-тами (событиями), не требующая затрат труда, материальных ресурсов и времени. Она указывает, что возможность начала одной работы непосредственно зависит от результата другой. Продолжительность фиктивной работы равна нулю.
Событие —это момент завершения какого-либо процесса.Событие можетявляться частным результатом отдельной работы или суммарным результатом нескольких работ. Конечный результат любой работы важен не только как факт окончания данной работы, но и как необходимое условие для начала следующих работ. Событие не имеет продолжительности во времени.
Сетевой график ограничен исходным и завершающим событиями. Исход-ное событие (источник) не имеет предшествующих работ и событий. Завер-шающее событие (сток) не имеет последующих работ и событий. У всех собы-
тий сети, кроме исходного и завершающего, имеются, по крайней мере, по од-ной непосредственно предшествующей и по одной непосредственно за ним сле-дующей работе. Событие, непосредственно предшествующее работе, по отно-шению к ней называется начальным, а событие, непосредственно следующее за ней, — конечным. Исходная информация о работах, которые требуется выпол-нить, должна содержать: 1) перечень всех работ; 2) последовательность их вы-полнения; 3) оценку каждой работы (продолжительность, стоимость и т. п.). Информация о некотором проекте может быть задана в виде структурной таб-лицы комплекса работ (табл. 2.3).
| Таблица 2.3.Исходная информация построения сетевого графика | |||||
| Работа | Опирается | Продолжитель- | Работа | Опирается | Продолжитель- |
| на работы | ность работы | на работы | ность работы | ||
| a 1 | — | a 8 | a 3 | ||
| a 2 | — | a 9 | a 4, a 5, a 7 | ||
| a 3 | а 1 | a 10 | a 4, a 5, a 7 | ||
| a 4 | а 1 | a 11 | a 6, a 9 | ||
| a 5 | а 2 | a 12 | a 6, a 9 | ||
| a 6 | а 2 | a 13 | a 8, a 10, a 11 | ||
| a 7 | а 3 |
Сетевой график строится следующим образом:
– кружками обозначаются события;
– стрелками, соединяющими события, обозначаются работы;
– сплошными стрелками изображаются действительные работы;
– пунктирными — ожидания и фиктивные работы.
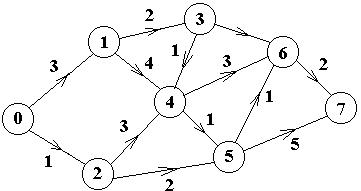
Построим сетевой график для последовательности работ, представленных в табл. 2.3. На предварительном этапе события, обозначающие начала или концы работ, можно нумеровать в произвольном порядке.
Пусть 0 — исходное событие. Работы a 1 и a 2 не имеют предшествующих работ, поэтому они выходят из исходного события.
На работу a 1 опираются работы a 3 и a 4, следовательно, в конце дуги, соответ-ствующей работе a 1, изображается событие, характеризующее ее окончание (номер 1), и из этого события выходят две дуги, отвечающие работам a 3 и a 4.
На работу a 2 опираются работы a 5 и a 6, следовательно, в конце дуги, соот-ветствующей работе a 2, изображается событие, характеризующее ее окончание (номер 2), из которого выходят две дуги, отвечающие работам a 5 и a 6.
На работу a 3 опираются работы a 7 и a 8, следовательно, в конце дуги, соот-ветствующей работе a 3, изображается событие, характеризующее ее окончание (номер 3), из которого выходят две дуги, отвечающие работам a 7 и a 8.
Работы a 9 и a 10 опираются на работы a 4, a 5 и a 7, поэтому необходимо объеди-нить концы дуг, соответствующие этим работам, в виде нового события (номер 4), а затем из события 4 изобразить три дуги, соответствующие работам a 4, a 5 и a 7.
Работы a 11 и a 12 опираются на работы a 6 и a 9, поэтому концы дуг, соответст-вующие работам a 6 и a 9, объединяются в виде очередного события (номер 5), и из события 5 изображаются две дуги, соответствующие работам a 11 и a 12.
Работа a 13 опирается на работы a 8, a 10 и a 11, поэтому концы дуг, соответст-вующие работам a 8, a 10 и a 11, объединяются в виде следующего события (номер 6), из которого изображается дуга, соответствующая работе a 13.
| Рис. 2.12.Сетевой график |
| с указанием ранних и поздних сроков |
| свершения событий |
| Рис. 2.11.Связь работы и событий |
| Начальное |
| событие |
| Конечное |
| событие |
| Работа (i, j) |
| i |
| j |
| tij |
| Рис. 2.10. Предварительный сетевой |
| график комплекса работ |
На работы a 12 и a 13 не опирается ни одна работа, поэтому их окончанием
служит завершающее событие (номер 7). Сетевой график изображен на рис. 2.10. Он выражает логическую связь в
последовательности событий и работ.
Для удобства работы с сетью по оп-ределению временных параметров необ-ходимо произвести упорядоченную нуме-рацию событий. События являются упо-рядоченными, если для каждой работы номер ее начального события меньше но-мера ее конечного события. Работу в се-тевых графиках принято кодировать па-рой (i, j), где i — номер начального, а j —

номер конечного события (рис. 2.11). В пронумерованной сети для каждой работы (i, j) всегда i < j. Продолжительность ра-боты tij принять проставлять в сетевом графике над соответствующей стрелкой.
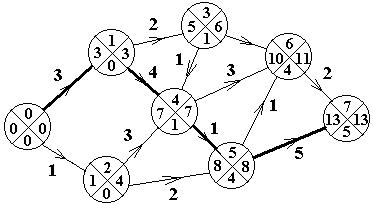
Пусть весь комплекс работ изобра-жен в виде пронумерованного сетевого графика (рис. 2.12) и известна продолжи-тельность tij каждой работы. Минималь-ное время, необходимое для выполнения всего комплекса работ, называется крити-ческим временем (t кр). Рассмотрим любой полный путь сетевого графика, т. е. путь от исходного события до завершающего события. Продолжительностью пути на-зывается время, необходимое для выпол-
нения всех работ, лежащих на этом пути. Обычно на сети существует несколько полных путей различной продолжительности. Нетрудно понять, что критическое время равно продолжительности самого длительного по времени полного пути. Такой путь называется критическим (L кр).Таким образом, полный путь сетевого графика, имеющий наибольшую длину, является критическим. В сети может быть несколько критических путей, имеющих одинаковую длину. Критический путь имеет особое значение в системе сетевого планирования, т. к. работы этого пути определяют общий цикл завершения всего комплекса работ.
Работы и события, лежащие на критическом пути, называются критическими, остальные работы и события сети будут некритическими. Если выполнение какой-либо критической работы будет задержано на некоторый срок, то это вызовет за-паздывание выполнения всего комплекса работ на тот же срок. Чтобы ускорить выполнение комплекса работ, необходимо сократить сроки выполнения критиче-ских работ. Некритические работы допускают некоторое запаздывание с их вы-полнением, и это не вызывает задержки срока реализации всего комплекса работ. Чтобы найти критический путь, критическое время и некоторые другие характери-стики сетевого графика, вводятся понятия раннего и позднего сроков свершения событий. Под свершением события понимается момент, к которому заканчивают-
ся все входящие в него работы, и может быть начата любая выходящая работа. Со-бытие может иметь некоторый интервал свободы свершения.
Математическое моделирование в задачах транспортного процесса. Ма-тематическая модель есть приближенное описание объекта(явления,процесса),выраженное с помощью математической символики. Общую схему математиче-ского моделирования можно изобразить в виде, представленном на рис. 2.13.
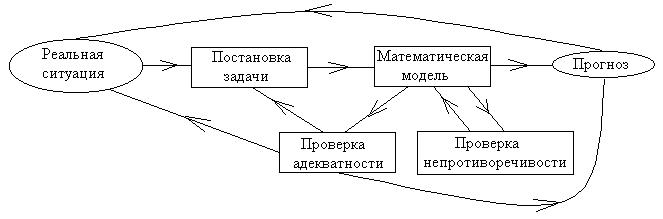
Рис. 2.13. Общая схема математического моделирования
Математическое моделирование имеет два существенных преимущества перед остальными видами моделирования:
– дает быстрый ответ на поставленный вопрос, на что в реальной обста-новке могут потребоваться иногда даже годы;
– дает возможность экспериментирования, осуществить которое на реаль-ном объекте зачастую просто невозможно.
В ходе моделирования можно получить ответы на бесчисленное число самых разнообразных вопросов. Постановка задачи и разработка математической модели требуют обращения к предметной области (управлению, проектированию, разра-ботке технологических процессов). Специалисты в предметной области, как пра-вило, прекрасно знают свой предмет, но обычно не имеют представления о том, что требуется для разработки модели и решения задачи на ЭВМ. Поэтому содер-жательная постановка задачи зачастую оказывается перенасыщенной сведениями, которые совершенно излишни для работы на ЭВМ.
В зависимости от характера изучаемых процессов в системе математиче-ские модели бывают:
• статические, отражающие поведение объекта в какой-либо момент време-ни (например, поперечный разрез объекта);
• динамические, отражающие поведение объекта во времени (временные ряды);
• детерминированные, отображающие детерминированные процессы, т. е. про-цессы, в которых предполагается отсутствие всяких случайных воздействий;
• стохастические, отображающие вероятностные процессы и события;
• дискретные, предназначенные для описания дискретных процессов;
• непрерывные, отражающие непрерывный характер процессов, протекаю-щих в системе;
• дескриптивные, служащие лишь для описания процессов функционирова-ния, протекающих в системе;
• оптимизационные, позволяющие управлять характеристиками процессов. Требования, предъявляемые к математическим моделям: адекватность, не-
противоречивость, универсальность, экономичность.
Основные требования к построению математических моделей информаци-онных систем:
Математическая модель должна отражать основные свойства исследуемого объекта с точки зрения интересующего параметра или группы параметров.
Математическая модель должна быть достаточно простой в содержательном смысле, т. е. результаты ее анализа должны быть легко интерпретируемы.
Математическая модель должна быть адаптированной под имеющиеся исходные данные.
Математическая модель должна быть легко модифицируемой при появле-нии новых исходных данных или сведений о внутренней природе системы.
Математическая модель информационной системы должна быть сфор-мулирована так, чтобы размерность этой модели позволяла бы проводить расче-ты на доступной вычислительной технике в разумные сроки.
Учитывая, что характеристики транспортных процессов полностью соответ-ствуют требованиям, предъявляемым в математическом моделировании, а также актуальность оптимизации транспортной логистики и сравнительно невысокие затраты при возможности проработки большого количества оптимизационных вариантов, использование математического моделирования в транспортных про-цессах безусловно необходимо. Например, задача логистической оптимизации материального потока лесоматериалов заключается в необходимости удовлетво-рения потребностей получателей лесоматериалов и обеспечить минимальные за-траты на поставку. Затраты на поставку включают закупку и транспортировку. Современный лесопромышленный комплекс часто организует холдинги, вклю-чающие сеть лесозаготовительных предприятий и лесоперерабатывающее пред-приятие, а также возможный лесной терминал.
Для формулирования математической модели введем ряд обозначений: i — количество лесозаготовительных предприятий (от 1 до m); k — количество по-требителей лесоматериалов (от 1 до n); j — количество лесных терминалов (от 1 до t); xij — грузопоток лесоматериалов от лесозаготовительных предприятий до j -го терминала; cij — стоимость перевозки1м3лесоматериалов от i -го лесозагото-вительного предприятия до j -го терминала; xjk — грузопоток лесоматериалов от j -го терминала до k -го потребителя; cik — стоимость перевозки1м3лесоматериа-лов от j -го терминала до k -го потребителя; cj — стоимость погрузочно-разгрузочных работ, хранения 1 м3 лесоматериалов; Xj — объем грузопереработ-ки лесоматериалов на j-м терминале, м3; Pi — объем лесоматериалов, поступаю-щий от i -го лесозаготовительного предприятия до j -го терминала; Qk — объем ле-соматериалов, потребляемый k -м потребителем, м3; Z — общие логистические издержки оптимальной организации грузопотоков лесоматериалов в холдинге.
С учетом выше приведенных условных обозначений математическая модель транспортной задачи логистической оптимизации грузопотоков лесоматериалов в холдинге заключается в минимизации общих логистических издержек:
| mt | t | tn | ||
| → min. | ||||
| Z =∑ ∑ cij xij +∑ c j x j +∑ k ∑ c jk x jk | ||||
| i =1 j =1 | j =1 | j =1 k =1 |
Ограничения:
t
P =∑ xij,характеризует объем лесоматериалов,поступающих с i- го лесо-
=1
заготовительного предприятия на j -й лесной терминал, м3.
t
Q =∑ x jk,характеризует потребность k -го потребителя в лесопродукции,м3.
=1
xij > 0; xjk > 0,что свидетельствует о том,что материальный поток можетбыть только положительным.
m n
∑ Pi = ∑ Qk, характеризует равенство объемов лесопродукции, отправ-
i =1 k =1
ляемой с лесозаготовительных предприятий на терминалы и с терминалов, при-нимается потребителями.
m n
X j =∑ xij =∑ x jk,свидетельствует о том,что объем грузопереработки на
i =1 j =1
j -м терминале равен грузопотоку лесоматериалов от i- го лесозаготовительногопредприятия до j -го терминала и равен грузопотоку лесоматериалов от j -го тер-минала до k- го потребителя.
Использование математического аппарата теории массового обслужива-ния в транспортных процессах. В логистическом управлении сервисными про-цессами можно использовать для оптимизации известную систему массового об-служивания, которая с помощью моделирования потоков позволяет решать задачи планирования производственной базы сервиса, а также организации самого про-цесса технического обслуживания и ремонта автомобилей наилучшим образом.
На основе использования математического аппарата теории массового об-служивания определяются закономерности формирования производительности
пропускной способности системы обслуживания. В результате использования этих методов представляется возможным оценивать надежность функциониро-вания способности производственно-технической базы, обеспечить интенсифи-кацию производства и повышение эффективности работы исполнителей и ис-пользования производственных мощностей. Обеспечение работоспособности автомобилей в предприятиях автомобильного транспорта осуществляет инже-нерно-техническая служба. Она производит планирование производством тех-нического обслуживания (ТО) и текущего ремонта (ТР) с учетом специализа-ции, концентрации и кооперации производства, обеспеченности трудовыми и материальными ресурсами, унификации и типизации технологических процес-сов и элементов производственно-технической базы, использования инструмен-тальных методов диагностирования и контроля технического состояния под-вижного состава автомобильного транспорта.
Состав предприятий и специализированных производств автотранспорта определяется перечнем основных и вспомогательных работ, выполняемых в процессе ТО и ТР автотранспортным предприятием. Системы, в которых пере-менными и случайными являются моменты поступления требований на обслу-живание и продолжительность самих обслуживании, называются системами массового обслуживания (СМО).В области технической эксплуатации автомо-билей к ним относятся: посты, линии, участки автотранспортных предприятий, автокомбинатов, объединений, баз централизованного технического обслужи-вания, станций технического обслуживания, склады запасных частей, агрегатов, механизмов и деталей, топливо- и маслораздаточные колонки АЗС, автомобили технической помощи и др. Система массового обслуживания состоит из элемен-тов: входящего потока требований, очереди, обслуживающих аппаратов и вы-ходящего потока требований. Под требованием понимается потребность в про-
ведении работ по ТО и ремонту автомобилей. Требование можно отождествлять с его носителем: автомобилем, агрегатом, механизмом, деталью.
Входящий поток требований представляет собой совокупность требованийна удовлетворение потребности в проведении технических воздействий. Заявки поступают в некоторые случайные моменты времени. Число требований, посту-пающих в систему за единицу времени, является случайной величиной, а входя-щий поток представляет собой случайный процент. Требования могут быть одно-родными и неоднородными. Так, например, поток требований на один вид ТО, с одной стороны, является однородным, с другой стороны, если поток образуется из технологически несовместимых групп автомобилей, он будет неоднородным.
Обслуживающие аппараты —это совокупность отдельных рабочих звень-ев, бригад, постов с необходимым оборудованием, средствами механизации, ин-струментом и оснасткой, запасе новых и отремонтированных агрегатов, узлов механизмов и деталей. Очередь образуется в том случае, когда пропускная спо-собность обслуживающих аппаратов недостаточна по отношению к величинам входящего потока требований.
Выходящий поток требований в зависимости от структуры и параметровСМО составляют обслуженные и не обслуженные требования.
СМО классифицируются следующим образом:
а) по длине очереди: с потерями, без потерь и с ограничением по длине очереди или времени нахождения в ней;
б) по количеству каналов обслуживания: одноканальные (все требования обслуживаются одним аппаратом) и многоканальные (требование может быть обслужено любым свободным аппаратом);
в) по типу обслуживающих аппаратов: однотипные (могут быть универсаль-ными или специализированными) и разнотипные (одновременно могут использо-ваться универсальные, специализированные и специальные аппараты);
г) по количеству фаз обслуживания: однофазные (требование обслуживается одним аппаратом за одну постановку) и многофазные (требование обслуживается последовательно несколькими аппаратами). Системами однофазовым обслужи-ванием являются отдельные посты, рабочие места, на которых выполняется пол-ный комплекс необходимых работ по техническому обслуживанию и ремонту. Примером СМО с многофазовым обслуживанием является поточная линия ТО, т. к. на отдельных постах выполняется только определенный перечень работ, а вы-полнение полного объема ТО проводится по всей поточной линии;
д) по порядку обслуживания: системы с приоритетом (например, первооче-редная заправка маршрутных автобусов и специальных машин на АЗС, первооче-редное проведение ремонта с малым объемом и др.) и без приоритета;
е) по структуре систем: замкнутые (входящий поток требований зависит от количества обслуженных требований) и открытые (входящий поток требований не зависит от количества обслуженных требований);
ж) по взаимопомощи: с взаимопомощью (пропускная способность и произ-водительность обслуживающих аппаратов будет зависеть от занятости других аппаратов) и без взаимопомощи (параметры пропускной способности и произ-водительности обслуживающих аппаратов постоянны и не зависят от простоя других аппаратов).
Входящий поток требований представляет собой поток автомобилей, агре-гатов, механизмов и деталей на проведение ТО и ремонта. Потоки требований
на ТО и ремонт не постоянны в течение суток, недели, месяца, года. В ходе производства сервисных услуг поступление автомобилей на посты технического обслуживания и ремонта всегда неравномерно, поэтому можно говорить, что поток требований — величина случайная. Требование на обслуживание возни-кает как объективная необходимость, подчиняющаяся определенным законо-мерностям теории надежности. Фактическая реализация этих требований в сис-теме ТО и ремонта являются ординарными и с отсутствием последействия. Ор-динарность означает, что вероятность возникновения на элементарном отрезке времени двух или более требований пренебрежимо мала по сравнению с длиной самого отрезка. Отсутствие последействия — это независимость потока от чис-ла ранее поступивших отказов и моментов их возникновения. Так как поток требований в систему ТО и ремонта формулируется от списочного количества автомобилей, то он является потоком с отсутствием последействия. Поток, от-вечающий требованию стационарной ординарности и отсутствия последейст-вия, является простейшим. Для простейшего потока вероятность возникновения определенного числа требований определяется законом Пуассона:
Pk (t) = (ω k ⋅ t) k e −ω t ,
где k = 0, 1, 2, … — число отказов, возникающих за время t; ω — параметр пото-ка отказов.
Для правильного функционирования ремонтного процесса оборудование и его пропускная технологическая способность должны наилучшим образом и в срок удовлетворять все поступившие заявки. Поэтому возникает еще одно на-правление логистического управления автосервисными процессами — это по-иск оптимальных решений входящих потоков требований (заявок) на обслужи-вание. Кроме того, распределение времени на текущий ремонт происходит по экспотенциальному закону распределения: например, на устранение мелких технических неисправностей будет затрачен небольшой отрезок времени, в то время как текущий ремонт большой сложности происходит редко. Таким обра-зом, рассмотрение во взаимосвязи операционного и логистического управления при производстве сервисных работ и услуг в автотранспортном предприятии предполагает расширение оптимизационных возможностей автотранспортного предприятия в направлении повышения своей конкурентоспособности.
Транспортно-экспедиционная фирма —