Виды функций и их графики

Понятие функции

Зависимость одной переменной у от другой х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией.

Общий вид функции: у = f(х),

где х – независимая переменная (аргумент), у – зависимая переменная (функция).

Область определения функции D(f) - множество, на котором задаётся функция. Другими словами: множество значений, которые может принимать аргумент.

Область значений функции E(f) - множество, состоящее из всех значений, которые принимает функция.

График функции – множество точек на координатной плоскости, координатами которых являются пары чисел (х; у), где х – значение аргумента, у – соответствующее ему значение функции.

Нули функции – значения аргумента, при которых функция равна 0.

Виды функций и их графики

ü Линейная функция y = kx + m

График функции – прямая.

Коэффициент k отвечает за угол наклона (k>0 – угол острый, k<0 – угол тупой, k=0 – горизонтальная прямая), m – за сдвиг графика вверх-вниз (m>0 – вверх, m<0 – вниз).

у = kx – частный случай линейной функции при m=0.

В этом случае график функции обязательно проходит через начало координат.

Свойства функции y = kx + m

1) D(f) = (-∞; +∞)

2) Возрастает, если k > 0; убывает, если k < 0

3) Не ограничена ни снизу, ни сверху

4) Нет ни наибольшего, ни наименьшего значений

5) E(f) = (-∞; +∞)

у = 3

у = -х - 1

у = х+1

ü Функция y = kx² (k ≠ 0) График функции – парабола.

Свойства функции y = kx² Если k > 0

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4)

k>0

y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

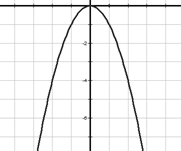
Если k < 0

1)

k<0

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; 0], убывает на луче [0; +∞)

3) Не ограничена снизу, ограничена сверху

4) y наим не существует, у наиб = 0

5) Непрерывна

6) E(f) = (-∞; 0]

ü Квадратичная функция y = ax² + bx + c

График функции – парабола, у которой:

® вершина располагается в точке (x0; y0), где x0 = , y0 = f(x0)

® ветви, направлены вверх, если а > 0, и вниз, если а < 0

® прямая х = х0 является ось ю симметрии параболы.

Число с – ордината точки пересечения параболы с осью Оу.

Свойства функции y = ax² + bx + c

Если а > 0

1) D(f) = (-∞; +∞)

2)

а>0

Убывает на луче (-∞; - ], возрастает на луче [- ; +∞)

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [y0; +∞)

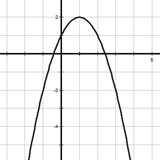Если а > 0

1)

а<0

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; - ], убывает на луче [- ; +∞)

3) Не ограничена снизу, ограничена сверху

4) y_наим не существует, у_наиб = 0

5) Непрерывна

6) E(f) = (-∞; y₀]

ü

k > 0

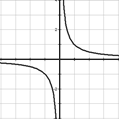Функция обратной пропорциональности y =

График функции – гипербола.

Свойства функции y =

1) D(f) = (-∞; 0) 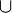(0; +∞)

2) Если k > 0, то функция убывает на промежутке (-∞; 0) (0; +∞)

k < 0

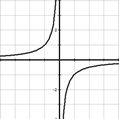Если k < 0, то функция возрастает на промежутке (-∞; 0) (0; +∞)

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Функция непрерывна на открытом луче (-∞; 0) и на открытом луче (0; +∞)

6) E(f) = (-∞; 0) (0; +∞)

ü Функция y =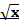

График функции – ветвь параболы, перевернутая «набок».

Свойства функции y =

1) D(f) = [0; +∞)

2) Возрастает

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

ü Функция y =

График функции – объединение двух лучей: y = x, x ≥ 0 и y = -x, x ≤ 0

Свойства функции y =

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

 

y = x ⁿ (n = 3, 5, 7, 9…)

График функции – кубическая парабола (при n=3)

Свойства функции

1)

n = 3

D(f) = (-∞; +∞)

2) Возрастает

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Непрерывна

6) E(f) = (-∞; +∞)

Преобразования графика функции y = f(x)

1) y = f(x) + a

Сдвиг вверх на а единиц, если a > 0

Cдвиг вниз, если a < 0

2) y = f(x + a)

Сдвиг влево на а единиц, если a > 0

Сдвиг вправо, если a < 0

3) - y = f(x)

Зеркальное отражение относительно Ох

4) y = f(-x)

Зеркальное отражение относительно Оу

5) y = a·f(x)

Растяжение вдоль Оу, если a > 1

Растяжение вдоль Ох, если 0 < a < 1

6) y = f(|x|)

Для x ≥ 0, y = f(x)

Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую.

7) y = |f(x)|

Для f(x) ≥ 0, |f(x)| = f(x)

Для f(x) < 0, |f(x)| = -f(x)

Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox.