Теорема: А 1, А 2,..., Аn образуют полную группу несовместных событий, то сумма их вероятностей равна 1.
Доказательство
А 1 + А 2 + А 3 +... + Аn – достоверное
P (A 1 +... + An) = 1.
А 1, А 2,..., An – несовместны.
Теорема сложения для несовместных событий.
Таким образом, P (A 1) + P (A 2) +... + P (An) = 1. ▲
Утверждение: 
Доказательство
А и 
несовместны, образуют полную группу.
пример 1. Производятся три выстрела по одной мишени. Вероятность попадания при 1ом, 2ом, 3ем выстрелах равны p 1 = 0,4; p 2 = 0,5; p 1 = 0,7. Найти вероятность того, что будет только одно попадание.
Решение
А – одно попадание из трех;
А 1 – попадание при 1ом выстреле;
А 2 – попадание при 2ом выстреле;
А 3 – попадание при 3ем выстреле.
пример 2. Стрелок А поражает мишень с вероятностью 0,6; стрелок B – 0,5 C – 0,4. Стрелки произвели одновременно выстрелы и две пули попали в цель. Что вероятнее попал стрелок С или нет?
Решение
А – попал А p 1 = 0,6
B – попал B p 2 = 0,5
C – попал C p 3 = 0,4
D – 2 попадания из трех.
Найти PD (C).
Вероятность появления хотя бы одного из событий А 1, A 2,..., An равна разности между 1 и вероятностью непоявления ни одного из событий.
пример. Сколько подбрасываний монеток нужно произвести, чтобы хотя бы один раз появился герб, если вероятность этого события должна быть не меньше 0,9375.
Решение
Пусть произведено n подбрасываний. Найдем вероятность, что герб выпадет хотя бы один раз.
А – герб выпадет хотя бы один раз.
– герб не выпадет ни разу.
Формула полной вероятности
Пусть В 1, В 2,..., Вn несовместны и образуют полную группу.
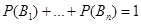
Назовем эти события гипотезами.
Пусть событие А может произойти только одновременно с одной из гипотез, тогда
– это формула полной вероятности.
Доказательство
А = В 1 А + В 2 А +... + BnA.
По теореме сложения для несовместных событий P (A) = P (B 1 A) +... + P (BnA).
По теореме умножения 
пример. В ящике лежит 20 теннисных мячей – 12 новых и 8 старых. Наугад извлекаются два мяча для игры. После чего их снова возвращают в ящик. Затем вынимают два мяча для второй новой игры. Найти вероятность, что они новые.
Решение
А – 2 мяча для 2ой игры – новые.
В 1 – для первой игры – 2 новых
В 2 – для первой игры – 1 новый и 1 старый
В 3 – для первой игры – 2 старых
По условию задачи всего 20 мячей – 12 новых и 8 старых.
Формула Бейеса
Пусть известны начальные вероятности гипотез (до опыта). Произвели опыт, в результате которого произошло событие А. Как изменяются вероятности гипотез.
Доказательство
пример. 5% мужчин и 0,25% женщин являются дальтониками. Произвольно выбранное лицо оказалось дальтоником, найти вероятность, что это мужчина.
Решение
B 1 – муж. В 2 – жен. А – дальтоник
Повторные испытания
Пусть проводятся n независимых испытаний, в каждом из которых событие А может произойти или не произойти. Вероятность появления А в каждом испытании постоянна и равна р. Тогда вероятность того, что А не произойдет в каждом испытании обозначим q и равна она: 
.
Требуется найти, что Pn (k) – вероятность того, что событие А появится k раз в n испытаниях.
В – А появилось k раз из n. 
k множителей из n можно разместить 
раз.
По теореме сложения: 
пример. Производится 5 подбрасываний монеты. Найти вероятность того, что герб выпадет а) не более 2 раз; б) не менее 2 раз.
Решение
!!! Формула Бернулли применяется для небольших n.
Асимптотические формулы n → ∞