Геометрическое пространство

БАЗОВЫЕ ГЕОМЕТРИЧЕСКИЕ ЗНАНИЯ

Геометрическим пространством принято считать бесконечное множе ство геометрических элементов. Например, прямую можно считать пространством, если она представляется как множество точек. Плоскость как пространство является множеством точек или прямых. Этот ряд примеров можно продолжать достаточно долго, что обеспечивается универсальностью определения пространства.

Распространенным способом образования пространства является кинематический. Суть его заключается в том, что некоторый элемент, например точка, прямая или плоскость, перемещаясь по какому-либо закону, образует это пространство. Например, результатом перемещения точки является линия. Прямолинейное перемещение образует прямую линию, криволинейное – кривую линию. Перемещение прямой или кривой линии образует плоскость или пространство и т. д.

Геометрическое пространство отличают следующие свойства, которые необходимо учитывать при работе с ним:

· относительность;

· абстрактность;

· размерность;

· проективность.

Относительность. Любой геометрический элемент может являться одновременно пространством, и наоборот, любое пространство может оказаться элементом. Здесь важно понять, что принцип относительности действует и в геометрии. Любое определение не является жестко фиксированным по отношению к определяемому объекту. Например, прямая может быть представлена как множество точек, тогда она представляет собой пространство. Если она мыслится как неделимый объект, тогда она может быть элементом плоскости или другого пространства.

Абстрактность. Геометрическое пространство является математическим объектом, и, как любой математический объект, оно не существует в реальной действительности.

Размерность. Одной из распространенных операций над геометрическими пространствами является выделение элемента этого пространства. Для этого в пространстве фиксируется система координат и намечается процедура соотнесения элементов с этой системой. В результате образуется некий набор чисел, который принято считать размерностью этого пространства.

Рассмотрим несколько примеров применительно к линейным пространствам. Положению произвольных точек А и В на прямой l (рис. 3) ставится в соответствие набор из одного числа. Это расстояние от выбранной точки до некоторой фиксированной точки О, играющей роль координатной системы. В результате прямая, как множество точек, представляет собой одномерное пространство.

 

Рис. 3. Выделение точки из множества точек прямой

 

Положению точки А в плоскости ставится в соответствие набор из двух чисел (рис. 4), которые считываются на координатных осях х и у. Процедура сопоставления заключается в проведении через точку прямых, параллельных осям координат. Множество точек плоскости – двухмерное пространство.

Рис. 4. Выделение точки из множества точек в плоскости

Положению точки А в трехмерном пространстве соответствует набор из трех чисел (рис. 5). Для того чтобы ее выделить, необходимо выполнить известную процедуру. Через заданную точку провести три плоскости α, β, γ. Каждая из этих плоскостей пересечет ось координат, которой она перпендикулярна, и выделит на ней точку. Расстояние от этой точки до начала координат измеряется конкретными числами аx, аy, аz. В результате получим три числа, которые позволяют выделить в трехмерном пространстве одну точку из бесконечного множества ей подобных.

.

Рис. 5. Выделение точки из множества точек в трехмерном пространстве

Исходя из требования рациональности, набор чисел должен быть минимальным. Это требование является непременным условием при выделении геометрического элемента из множества ему подобных. Поэтому, выделяя одну прямую из множества прямых плоскости, достаточно набора из двух чисел, поскольку положение прямой определяется двумя точками, но взять их нужно на координатных осях (рис. 6). В результате плоскость, как множество прямых, оказывается двухмерным пространством.

Положение прямой в трехмерном пространстве соответствует набору из четырех чисел, так как две ее точки целесообразно взять в координатных плоскостях (рис. 7). Следовательно, множество прямых трехмерного пространства образует четырехмерное пространство. Возникающая здесь риторическая тавтология связана с традицией в наименовании пространств, но она не искажает существо рассматриваемой ситуации.

 

Рис. 6. Выделение одной прямой из множества прямых в плоскости

Рис. 7. Выделение одной прямой из множества прямых трехмерного пространства

Три точки, определяющие положение плоскости в трехмерном пространстве, лучше всего выбрать на координатных осях. Таким образом, положению плоскости в пространстве соответствуют три числа (рис. 8).

 

 

Рис. 8. Выделение одной плоскости из множества плоскостей трехмерного пространства

Очевидно, что этот ряд примеров можно продолжать достаточно долго, и в каждом случае положение элемента в пространстве соответствует набору чисел. С этим соответствием связано понятие о размерности пространства. Сколько чисел входит в набор, такова и размерность пространства. Таким образом, прямолинейный ряд точек имеет размерность, равную единице (R ¹), плоское поле точек и прямых двумерно (R²), трехмерное пространство (R ³) как множество точек имеет размерность, равную трем, но как множество прямых оно уже четырехмерно (R ⁴).

Обобщая сказанное, можно сделать вывод: размерность – это минимальный набор чисел, который определяет положение элемента в пространстве.

Проективность. Основная цель, которая определяла необходимость создания геометрии как науки – конструирование геометрических моделей реальности. Историческая ретроперспектива показывает, что период ее существования накопил много вариантов геометрии, которые описывают те или иные аспекты реальности. Это геометрии Евклида, Лобачевского, Римана (многомерная, аффинная и проективная геометрии). Следует заметить, что глаз человека устроен так, что он не видит параллельных объектов. Поэтому для описания процесса возникновения изображений, аналогичных тем, которые видит глаз человека, целесообразно использовать проективную геометрию. Она, как и глаз человека, не видит различия между параллельными и непараллельными объектами. Геометрическое пространство в этой геометрии обладает свойством проективности. Его обеспечивает наличие бесконечно удаленных элементов. Чтобы понять, что это такое, рассмотрим пример на рис. 9.

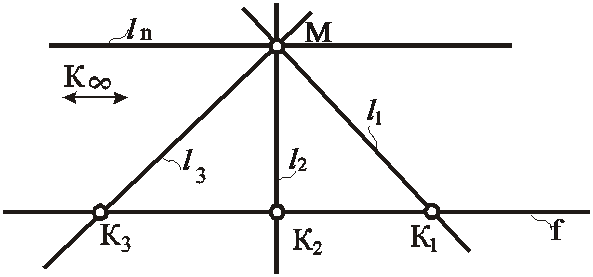
Рис. 9. Выявление бесконечно удаленной точки прямой

 

В плоскости зафиксированы точка М и прямая f. Через точку М проведем прямую l, которая пересечет прямую f в точке К. Вращая прямую l вокруг точки М по часовой стрелке (можно и против часовой стрелки), будем следить за движением точки К. Она пробежит по всем точкам прямой f. В случае, когда прямя l окажется параллельной прямой f, мы увидим точку К в бесконечности, если посмотрим влево. Если посмотрим право, то также увидим общую точку этих прямых. Но здесь возникает парадоксальная ситуация: известно, что две не совпавшие прямые имеют только одну общую точку. А у нас их две. Это противоречит одному из базовых положений геометрии Евклида. Чтобы ликвидировать это противоречие, объединим эти точки в одну. В результате получим проективную прямую, которая оказывается замкнутой на бесконечности одной точкой. В этой точке с ней будут пересекаться и другие параллельные ей прямые. Таким образом, все прямые, которые лежат в одной плоскости, пересекаются друг с другом. Только точки пересечения параллельных прямых находятся в бесконечности.

Повысим размерность всех элементов на единицу. В результате получим конструкцию, которая состоит из двух плоскостей ά, β и двух прямых m, k (рис. 10). Плоскость β будем вращать вокруг прямой m и следить за перемещением прямой k. В случае, когда плоскости ά и β станут параллельными друг другу, прямая k уйдет в бесконечность. Плоскость ά (как и плоскость β ) окажется замкнутой на бесконечности одной прямой. По этой прямой будут пересекаться все плоскости параллельные ά и β. Таким образом, все плоскости, которые принадлежат одному трехмерному пространству, пересекаются друг с другом. Только линии пересечения параллельных плоскостей находятся в бесконечности.

 

Рис. 10. Выявление бесконечно удаленной прямой плоскости

 

Символическая запись выявленной ситуации выглядит следующим образом:

R¹ É одна R⁰,

R² É одна R¹,

R³ É одна R²,

…………………

Rⁿ É одно R^n-1.

 

Она позволяет логически обобщить принадлежность бесконечно удаленных элементов их пространствам. Словесное описание этой символической записи выглядит так:

· прямая, как проективное пространство, содержит одну бесконечно удаленную точку;

· плоскость, как проективное пространство, содержит одну бесконечно удаленную прямую;

· трехмерное проективное пространство содержит одну бесконечно удаленную плоскость.

Обобщая сказанное, дадим определение проективному пространству.

Проективное геометрическое пространство содержит одно бесконечно удаленное подпространство, размерность которого на единицу меньше размерности самого пространства.

В существующей литературе бесконечно удаленные элементы еще называют несобственными.

Между пространствами или их элементами существует два типа отношений: позиционные и метрические.

Позиционные отношения геометрических элементов возникают тогда, когдаони характеризуются без применения чисел, а только с использованием таких терминов, как “принадлежит”, “пересекается”, “объединяется” и т.п. Выявление позиционных характеристик связано с решением позиционных задач, таких, как установление принадлежности элементов пространству или выявление третьего элемента (пространства), который является результатом расположения двух данных элементов (пространств). Например, очень распространенной задачей является установление принадлежности точки к прямой, плоскости или поверхности; линии к плоскости или поверхности. Очень часто встречаются задачи на объединение двух элементов (пространств): через две точки нужно провести прямую, через три точки – плоскость и т.д. Результатом взаимного расположения пространств может быть точка пересечения прямой с плоскостью или поверхностью, а также линия пересечения двух поверхностей и т.п. Целесообразно поделить все позиционные задачи на две группы:

1) выявление взаимной принадлежности элемента и пространства;

2) определение третьего пространства (элемента) как результата расположения двух данных.

Первая группа задач является наиболее простой и лежит в основе решения второй группы задач. Основными операциями, которые приходится выполнять при решении этих задач, являются пересечение и объединение. Используя символическую запись, данную в таблице, можно очень подробно записать решение любой задачи.

Метрические отношения геометрических элементов возникают тогда, когда к оценке их взаимного расположения привлекаются числа. Для их выявления решаются такие метрические задачи, как определение расстояния от одного элемента до другого, угла между двумя элементами и натуральной величины плоской фигуры.

Задача освоения приемов работы с геометрическими моделями конкретизируется в решении позиционных и метрических задач (рис. 1). Алгоритмы решения указанных задач нашли практическое применение в построении теней (позиционные задачи) и разверток (метрические задачи).

Решение как позиционных, так и метрических задач представляет собой последовательность действий (алгоритм). Эту последовательность целесообразно записывать. Запись может быть текстовая и символическая. Последняя отличается лаконичностью и образностью. В таб. 1 даны условные обозначения элементов пространства и их отношений.

Геометрические пространства могут иметь различную организацию. Традиционно некоторые из них имеют названия. Множество точек прямой называется прямолинейным рядом точек. Точки, заполняющие кривую линию, образуют криволинейный ряд точек. Плоскость как множество точек называется плоским полем точек, а как множество прямых - плоским полем прямых.

Если в плоскости зафиксировать точку, то множество прямых, принадлежащих ей, образует пучок прямых. В случае, когда точка зафиксирована в трехмерном пространстве, то множество прямых, проходящих через нее, образует связку прямых. Множество плоскостей, принадлежащих фиксированной точке трехмерного пространства, образует связку плоскостей. Множество плоскостей, содержащих одну фиксированную прямую, образует пучок плоскостей.

 

 

Условные обозначения

 

Таблица 1

 

Элементы пространства или отношения элементов	Условные обозначения	Примеры
Точки	Прописные буквы латинского алфавита	А, B, C....
Линии	Строчные буквы латинского алфавита	a, b, c,...
Плоскости, поверхности, углы	Строчные буквы греческого алфавита	a, b, g,...
Тождественное совпадение элементов	º	А º В
Принадлежность одного элемента другому	É, Ì	А Ì a, l É М
Пересечение элементов	Ç	m Ç n
Объединение элементов	È	M È f
Непересечение элементов		k r
Результат операции	=	m Ç n = К

 

Контрольные вопросы

1. Дать определение геометрического пространства.

2. Как объяснить относительность геометрического пространства?

3. Почему геометрическое пространство абстрактно?

4. Что такое размерность геометрического пространства?

5. Какое пространство считают проективным?

6. Какие отношения геометрических элементов считают позиционными?

7. Какие отношения геометрических элементов считают метрическими?

8. Что такое прямолинейный ряд точек?

9. Что такое криволинейный ряд точек?

10. Какое множество называют плоским полем точек?

11. Что такое пучок прямых?

12. Какое множество называют пучком плоскостей?

13. Что такое связка прямых?

14. Какое множество называют связкой плоскостей