Лабораторная работа №1. 1.

Тема: Однофазные цепи переменного тока с последовательным соединением элементов.

Цель: Экспериментальное исследование однофазных цепей переменного тока с последовательным соединением элементов и практическое определение их параметров.

Основные сведения.

В цепях постоянного тока все проводники обладают электрическим сопротивлением, которое принято называть омическим. В цепях переменного тока имеют место следующие виды сопротивлений: активное – R; реактивное – X и полное – Z. Геометрическую интерпретацию связи между ними даёт треугольник сопротивлений (рисунок 18), из которого следуют соотношения:

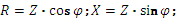
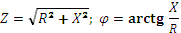
Активным сопротивлением обладают элементы, в которых электрическая энергия необратимо преобразуется в тепловую, световую, механическую т.д. (резисторы, лампы накаливания, электронагревательные приборы и др.). Реактивным сопротивлением обладают элементы способные запасать энергию в магнитном или электрическом полях, например, катушки индуктивности и конденсаторы. По своей физической природе реактивное сопротивление отличается от активного, и оно обусловлено влиянием магнитного и электрического полей, связанных с цепью.

При постоянном токе магнитный поток, создаваемый катушкой индуктивности, в установившемся режиме постоянен, сопротивление катушки невелико, так как обусловлено только омическим сопротивлением провода обмотки. При переменном токе магнитный поток в катушке изменяется во времени, и согласно закону электромагнитной индукции в катушке индуктируется э.д.с. противоиндукции, препятствующая изменению тока. За счёт этой э.д.с. катушка индуктивности оказывает противодействие переменному току, характеризующееся величиной индуктивного сопротивления: 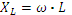, где 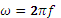- угловая (циклическая) частота переменного тока; L – индуктивность.

При постоянном напряжении, заряд конденсатора постоянен: 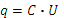, где С – ёмкость конденсатора. Активное сопротивление конденсатора бесконечно велико за счёт прослойки диэлектрика между его обкладками. Переменное напряжение создаёт изменяющийся во времени заряд, и в диэлектрике возникает ток смещения 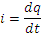. Противодействие конденсатора переменному току характеризуется величиной ёмкостного сопротивления: .

В отличие от активного, индуктивное и ёмкостное сопротивления не связаны с преобразованием электрической энергии в энергию другого вида, за что получили название реактивных.

В общем случае, когда участок цепи содержит последовательно соединённые индуктивность и ёмкость, его реактивное сопротивление равно разности индуктивного и ёмкостного сопротивлений: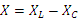

Реактивное сопротивление – величина алгебраическая и его знак определяется тем, какое из сопротивлений (индуктивное или ёмкостное) преобладает. При 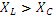величина 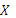положительна, при 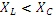– отрицательна.

При заданном напряжении действующее значение тока определяется формулой: , выражающей закон Ома для участка цепи переменного тока.

Энергетические процессы в цепях переменного тока имеют особенности по сравнению с цепями постоянного тока. Помимо необратимого преобразования электрической энергии в энергию другого вида в них наблюдается процесс обратимого преобразования электрической энергии. При возрастании синусоидального тока (а, следовательно, и магнитного потока) в индуктивности электрическая энергия преобразуется и накапливается в виде энергии магнитного поля, которая достигает максимума при максимальном значении тока. При убывании тока энергия магнитного поля преобразуется в электрическую и возвращается в цепь, т.е. происходит периодический обмен энергией между магнитным полем индуктивности и цепью. Подобное преобразование электрической энергии в энергию электрического поля наблюдается в ёмкости при приложенном синусоидальном напряжении. При возрастании напряжения конденсатор потребляет энергию (заряжается) из цепи, запасая её в электрическом поле. При убывании напряжения конденсатор, разряжаясь, отдаёт энергию обратно в цепь.

При анализе энергетических процессов в цепях переменного тока используются четыре понятия мощности:

· Мгновенная мощность: , где 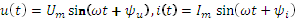- мгновенные значения напряжения и тока, изменяющиеся во времени по синусоидальному закону. Мгновенная мощность даёт значение мощности, потребляемой участком цепи в произвольный момент времени.

· Активная мощность: 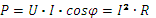, где и действующие значения напряжения и тока; 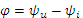– сдвиг по фазе между напряжением и током; - коэффициент мощности. Активной мощностью оценивается средняя за период скорость необратимого преобразования электрической энергии в энергию другого вида. Активная мощность измеряется в ваттах (Вт).

· Реактивная мощность: 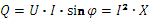. Понятие реактивной мощности, применяется для оценки процессов обмена энергией между электрическим и магнитным полями участка цепи и внешней цепью. Реактивная мощность измеряется в вольт-амперах реактивных (вар).

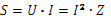· Полная мощность: . Полной мощностью называют расчётную величину, характеризующую пропускную способность участка цепи. Полная мощность измеряется в вольт-амперах (ВА).

Коэффициент мощности показывает, в какой степени используется пропускная способность участка цепи.

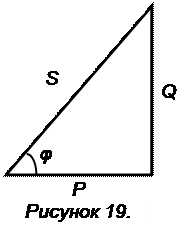
Активная, реактивная и полная мощности связаны соотношениями, которые следуют из треугольника мощностей (рисунок 19) подобного треугольнику сопротивлений: .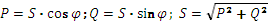

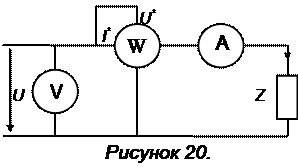Значения активной, реактивной, полной мощностей и параметров участка цепи могут быть экспериментально определены с помощью ваттметра, амперметра и вольтметра, включенных по схеме, показанной на рисунке 20 (ваттметр измеряет активную мощность, амперметр и вольтметр – действующие значения тока и напряжения). Используя показания приборов, можно рассчитать остальные параметры по формулам:

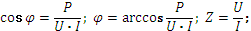
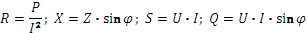
Анализ цепей переменного тока, как правило, сопровождается построением векторной диаграммы, представляющей совокупность векторов, изображающих синусоидально изменяющиеся во времени токи и напряжения. При построении векторной диаграммы длины векторов берут равными (в принятых масштабах) действующим значениям величин, а углы между ними – соответствующим сдвигам фаз.

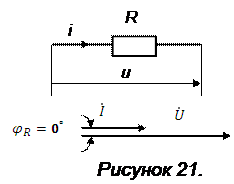Резистор представляет собой активную нагрузку, так как влияние индуктивности и ёмкости в нём настолько мало, что им можно пренебречь. Ток в активном сопротивлении и напряжение на нём совпадают по фазе, т.е. угол сдвига фаз: 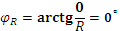. На векторной диаграмме для участка цепи, содержащего резистор (рисунок 21) векторы тока и напряжения сонаправлены.

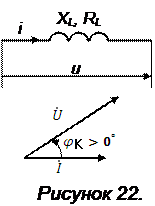Реальная катушка индуктивности – нагрузка активно-индуктивного характера, так как вследствие потерь мощности на нагрев провода обмотки она обладает помимо индуктивного сопротивления X_L активным сопротивлением R_L. Угол сдвига фаз между током в катушке индуктивности и напряжением на ней: 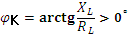, т.е. ток в индуктивности отстаёт от напряжения на ней. На векторной диаграмме для участка цепи, содержащего катушку индуктивности (рисунок 22), вектор напряжения повернут относительно вектора тока против часовой стрелки на угол .

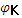В реальном конденсаторе при низких частотах (≤ 50 Гц) практически отсутствуют потери мощности и его можно рассматривать как ёмкостную нагрузку. Угол сдвига фаз между током в конденсаторе и напряжением на нём 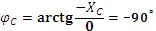, т.е. ток в конденсаторе опережает напряжение на угол . На векторной диаграмме для участка цепи, содержащего конденсатор (рисунок 23), вектор напряжения повернут относительно вектора тока по часовой стрелке на угол .

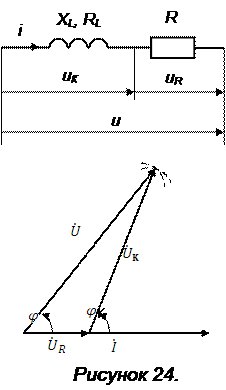Качественная векторная диаграмма для цепи, содержащей последовательно соединённые катушку индуктивности и резистор, представлена на рисунке 24. После выбора масштаба по току (М_I = … А/см) и масштаба по напряжению (М_U = … В/см) начинают построение диаграммы с вектора тока, так как при последовательном соединении элементов на всех участках цепи ток один и тот же. Затем, в принятом масштабе строят векторы напряжений на резисторе 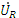, на катушке , используя при этом значения углов сдвига фаз для этих участков. Напряжение на входных зажимах в соответствии со вторым законом Кирхгофа должно удовлетворять условию:

Положение концов векторов и 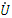можно определить способом засечек. Угол φ есть сдвиг по фазе между напряжением и током на входе цепи. Аналогично строится векторная диаграмма для цепи, содержащей последовательно соединённые резистор и конденсатор.