В 1881 г. Липпман (1845-1921), исходя из термодинамических соображений, предсказал обратный пьезоэлектрический эффект, который в том же году и был обнаружен братьями Кюри на кристаллах кварца. Обратный пьезоэлектрический эффект состоит в том, что при внесении пьезоэлектрического кристалла в электрическое поле в кристалле возникают механические напряжения, под действием которых кристалл деформируется.
Допустим, что кварцевая пластинка (см. рис. 4) внесена в электрическое поле, направленное параллельно оси  . Пусть она в направлениях
. Пусть она в направлениях  и
и  поддержана также действию механических натяжений
поддержана также действию механических натяжений  и
и  соответственно. Если
соответственно. Если  - объем пластинки, то элементарная работа, которую надо затратить на ее поляризацию при квазистатическом процессе, определяется выражением
- объем пластинки, то элементарная работа, которую надо затратить на ее поляризацию при квазистатическом процессе, определяется выражением  . Элементарная же механическая работа, совершаемая квазистатическими силами натяжения при удлинении ребер
. Элементарная же механическая работа, совершаемая квазистатическими силами натяжения при удлинении ребер  и
и  , будет
, будет  . Применим к рассматриваемому процессу термодинамическое соотношение
. Применим к рассматриваемому процессу термодинамическое соотношение  . Разделив его на
. Разделив его на  и обозначив через
и обозначив через  и
и  значения удельной энтропии и внутренней энергии, получим
значения удельной энтропии и внутренней энергии, получим
 ,
,
Или
 .
.
Введя функцию  , преобразуем это соотношение к виду
, преобразуем это соотношение к виду
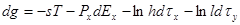 .
.
Так как выражение справа есть полный дифференциал функции  , то должно быть
, то должно быть
 ,
,
 .
.
или с учетом соотношения (1)
 ,
, 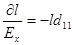 . (2).
. (2).
Эти формулы и описывают обратный пьезоэлектрический эффект в кварце. В линейном приближении, в котором только и верна излагаемая теория, формулы (2) записываются в виде
 , (3).
, (3).
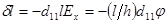 . (4).
. (4).
где  и
и  — абсолютные приращения размеров пластинки при наложении электрического поля
— абсолютные приращения размеров пластинки при наложении электрического поля 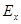 ,a
,a  - разность потенциалов между гранью
- разность потенциалов между гранью  и гранью, ей противоположной (рис. 4).
и гранью, ей противоположной (рис. 4).
Формула (3) выражает продольный обратный пьезоэлектрический эффект, а формула (4)- поперечный. При наложении электрического поля параллельно электрической оси меняется толщина пластинки (продольный эффект) и се длина (поперечный эффект). Если толщина 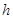 увеличивается, то длина
увеличивается, то длина 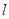 уменьшается, и наоборот, причем относительные изменения этих размеров по абсолютной величине одинаковы, так что объем пластинки остается неизменным. Абсолютное значение
уменьшается, и наоборот, причем относительные изменения этих размеров по абсолютной величине одинаковы, так что объем пластинки остается неизменным. Абсолютное значение  не зависит от толщины пластинки, а только от приложенной разности потенциалов
не зависит от толщины пластинки, а только от приложенной разности потенциалов  . При
. При  СГСЭ-ед. из формулы (3) находим
СГСЭ-ед. из формулы (3) находим  . Если
. Если  , то поперечный эффект при той же разности потенциалов будет в 10 раз больше. Модуль Юнга (1773-1829) кварца в направлении электрической оси
, то поперечный эффект при той же разности потенциалов будет в 10 раз больше. Модуль Юнга (1773-1829) кварца в направлении электрической оси  . При толщине пластинки
. При толщине пластинки  в ней в случае продольного эффекта в приведенном выше примере возникают натяжения или давления
в ней в случае продольного эффекта в приведенном выше примере возникают натяжения или давления  .
.
Термодинамические рассуждения, изложенные выше, проведены в предположении, что температура остается постоянной. Поэтому пьезоэлектрический модуль  может быть охарактеризован как изотермический модуль. Нетрудно видеть, как следует изменить эти рассуждения применительно к адиабатическим процессам. Формулы (1), (3) и (4) остаются верными и для таких процессов. Только изотермический пьезоэлектрический модуль
может быть охарактеризован как изотермический модуль. Нетрудно видеть, как следует изменить эти рассуждения применительно к адиабатическим процессам. Формулы (1), (3) и (4) остаются верными и для таких процессов. Только изотермический пьезоэлектрический модуль  надо заменить адиабатическим.
надо заменить адиабатическим.