1. C помощью 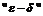 рассуждений доказать, что
рассуждений доказать, что
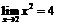 .
.
Заполнить следующую таблицу:
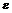
| 0,1 | 0,01 | 0,001 | 0,0001 | … |
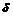
|
2. На языке 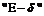 доказать, что
доказать, что
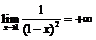 .
.
Заполнить следующую таблицу:
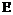
| … | ||||
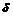
|
Сформулировать с помощью неравенств следующие утверждения:
3. а) 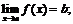 б)
б) 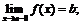 в)
в) 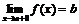 .
.
4. а) 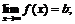 б)
б) 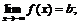 в)
в) 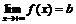 .
.
5. а) 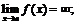 е)
е) 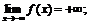
б) 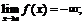 ж)
ж) 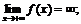
в) 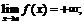 з)
з) 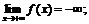
г) 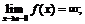 и)
и) 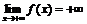 .
.
д) 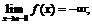
6. а) 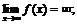 е)
е) 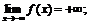
б) 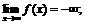 ж)
ж) 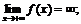
в) 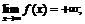 з)
з) 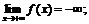
г) 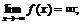 и)
и) 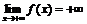 .
.
д) 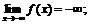
7. Пусть 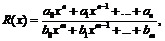
где 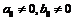 . Доказать, что
. Доказать, что 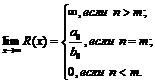
Найти значение следующих выражений:
8. а) 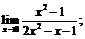 б)
б) 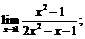 в)
в) 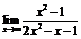 .
.
9. 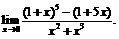 10.
10. 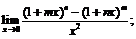
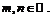
11.  12.
12. 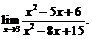
13. 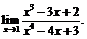 14.
14. 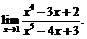
15. 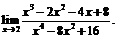 16.
16. 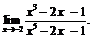
17. 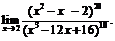 18.
18. 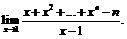
19. 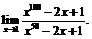 20.
20. 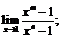
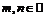 .
.
21. 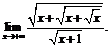 22.
22. 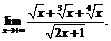
23. 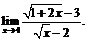 24.
24. 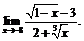
25. 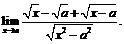 26.
26. 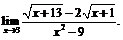
27.  28.
28. 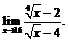
29. 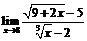 . 30.
. 30. 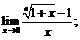
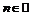 .
.
31. 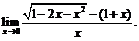 32.
32. 
33. 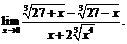 34.
34. 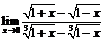 .
.
35. 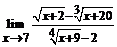 . 36.
. 36. 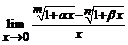 ;
; 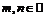 . 37.
. 37. 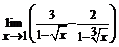 . 38.
. 38. 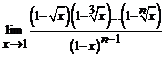 . 39.
. 39. 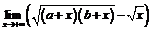 . 40.
. 40. 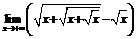 .
.
41. 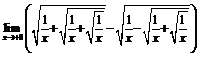 .
.
42. 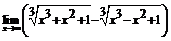 . 43.
. 43. 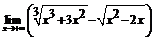 . 44.
. 44. 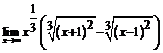 . 45.
. 45. 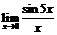 . 46.
. 46. 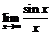 .
.
47. 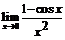 . 48.
. 48. 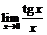 . 49.
. 49. 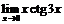 .
.
50. 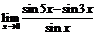 . 51.
. 51. 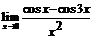 .
.
52. 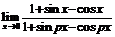 . 53.
. 53. 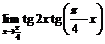 . 54.
. 54. 
55. Доказать равенства: a) 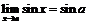 , б)
, б) 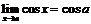 , в)
, в) 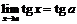 ,
, 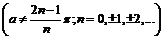 .
.
Найти пределы:
56. 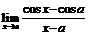 . 57.
. 57. 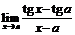 . 58.
. 58.  .
.
59. 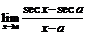 . 60.
. 60. 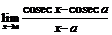 .
.
61. 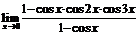 . 62.
. 62. 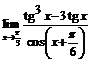 .
.
63. 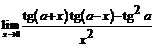 . 64.
. 64. 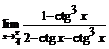 .
.
65. 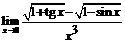 . 66.
. 66. 
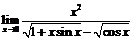 .
.
67. 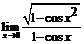 . 68.
. 68. 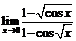 .
.
69.  .
.
70. а) 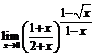 , б)
, б)  , в)
, в) 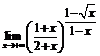 .
.
71. 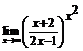 . 72.
. 72. 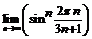 . 73.
. 73. 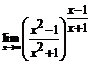 . 74.
. 74. 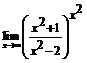 . 75.
. 75. 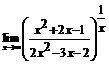 . 76.
. 76. 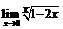 .
.
77. 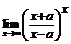 . 78.
. 78. 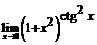 . 79.
. 79.  . 80.
. 80. 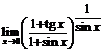 . 81.
. 81. 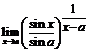 . 82.
. 82. 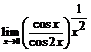 .
.
83. 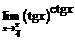 . 84.
. 84. 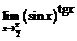 . 85.
. 85. 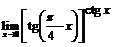 .
.
86. 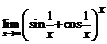 . 87.
. 87.  . 88.
. 88. 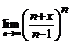 .
.
89. 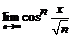 . 90.
. 90. 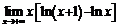 . 91.
. 91. 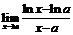 (a >0). 92.
(a >0). 92. 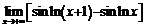 . 93.
. 93. 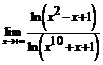 .
.
94. 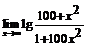 . 95.
. 95. 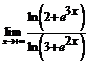 . 96.
. 96.  .
.
97. 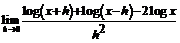 (x >0). 98.
(x >0). 98. 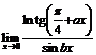 .
.
99. 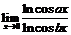 100.
100. 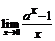 (a >0). 101.
(a >0). 101. 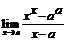 (a >0). 102.
(a >0). 102. 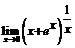 . 103.
. 103. 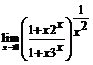 .
.
104. 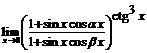 . 105.
. 105. 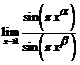 .
.
106. 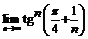 . 107.
. 107. 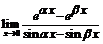 .
.
108. 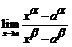 (a >0). 109.
(a >0). 109. 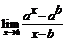 (a >0).
(a >0).
110. 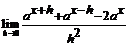 (a >0). 111.
(a >0). 111. 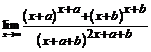 . 112.
. 112. 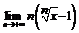 (x >0). 113.
(x >0). 113. 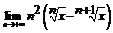 (x >0).
(x >0).
114. 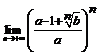 (a >0, b >0). 115.
(a >0, b >0). 115.  (a >0, b >0). 116.
(a >0, b >0). 116. 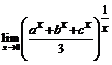 (a >0, b >0, c >0).
(a >0, b >0, c >0).
117. 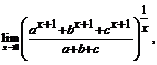 (a >0, b >0, c >0).
(a >0, b >0, c >0).
118. 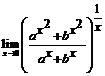 (a >0, b >0). 119.
(a >0, b >0). 119. 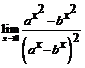 (a >0, b >0).
(a >0, b >0).
120. a) 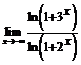 ; б)
; б) 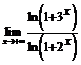 .
.
121. 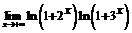 . 122.
. 122. 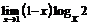 .
.
О-символика. Сравнение функций
Определение 1.
Функция 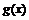 называется ограниченной по сравнению с функцией
называется ограниченной по сравнению с функцией 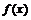 при
при  , если существует такая
, если существует такая
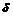 -окрестность точки
-окрестность точки 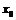 и такая постоянная
и такая постоянная  что как только
что как только 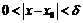 , тотчас выполняется
, тотчас выполняется 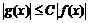 .
.
Для введенного понятия используется следующее обозначение: 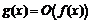 при
при  (читается так: «
(читается так: «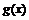 есть
есть 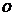 большое от
большое от 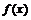 при
при  »).
»).
Знак  имеет здесь иной смысл, чем обычно, он лишь указывает на то, что рассматриваемое свойство имеет место только в некоторой окрестности точки
имеет здесь иной смысл, чем обычно, он лишь указывает на то, что рассматриваемое свойство имеет место только в некоторой окрестности точки 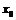 , но ни о каком пределе речь не идет.
, но ни о каком пределе речь не идет.
Аналогично определяется смысл записи 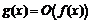 при
при 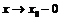 ,
, 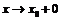 , x→∞, x→+∞, x→–∞.
, x→∞, x→+∞, x→–∞.
Если 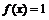 , то запись
, то запись 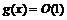 ,
,  означает, что в некоторой проколотой окрестности точки
означает, что в некоторой проколотой окрестности точки 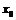 функция
функция 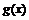 ограничена.
ограничена.
Пример 1. Верно ли: 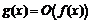 ,
,  , если
, если
1) 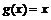 ,
, 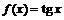 ,
,  ;
;
2) 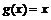 ,
, 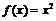 ,
, 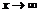 .
.
1) Используя известное неравенство 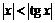 при
при 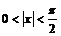 , получаем, что постоянное
, получаем, что постоянное 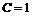 ,
, 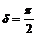 . Верно.
. Верно.
2) Для 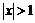 имеем:
имеем: 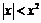 , следовательно, функция
, следовательно, функция 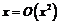 при
при 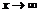 , хотя функция
, хотя функция 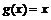 не является ограниченной при
не является ограниченной при 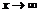 , она ограничена по сравнению с функцией
, она ограничена по сравнению с функцией 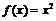
 .
.
Определение 2.
Если 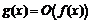 ,
,  , а
, а 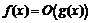 ,
,  , то функции
, то функции 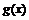 и
и 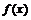 называются функциями одного порядка при
называются функциями одного порядка при  . В этом случае пишут:
. В этом случае пишут: 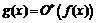 ,
,  .
.
Теорема.
Для того чтобы функции 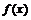 и
и 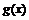 были функциями одного порядка при
были функциями одного порядка при  , достаточно, чтобы при
, достаточно, чтобы при  существовал конечный и не равный нулю предел отношения этих функций:
существовал конечный и не равный нулю предел отношения этих функций: 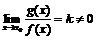 .
.
Пример 2. Какие из следующих пар функций являются функциями одного порядка при  :
:
1) 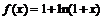 ,
, 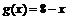 ;
;
2) 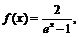
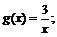
3) 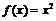 ,
, 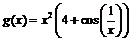 ;
;
4) 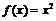 ,
, 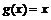 .
.
1) Так как 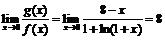 , то
, то 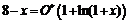 ,
,  .
.
2) Учитывая, что 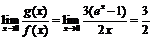 , имеем:
, имеем: 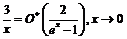 . Отметим, что при
. Отметим, что при  обе функции являются бесконечно большими.
обе функции являются бесконечно большими.
3) 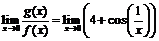 не существует. Однако же данные функции являются при
не существует. Однако же данные функции являются при  функциями одного порядка. Действительно, так как
функциями одного порядка. Действительно, так как  при
при 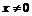 , то
, то 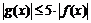 , то есть
, то есть 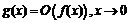 . С другой стороны,
. С другой стороны, 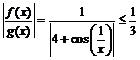 ,
, 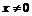 , то есть
, то есть 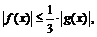 и
и 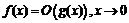 . Итак,
. Итак, 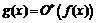 ,
, 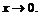
4) Воспользоваться теоремой нельзя, так как 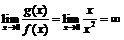 .
.
Данные функции не являются функциями одного порядка при  , так как, какова бы ни была постоянная
, так как, какова бы ни была постоянная  , неравенство
, неравенство 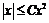 ,
, 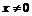 не выполняется ни в какой окрестности точки
не выполняется ни в какой окрестности точки 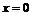 , и функция
, и функция 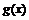 не является ограниченной по сравнению с функцией
не является ограниченной по сравнению с функцией 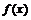 при
при  .
.
Отметим, что пример 2.3 показывает: существование конечного предела 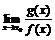 достаточное, но не является необходимым условием того, что функции
достаточное, но не является необходимым условием того, что функции 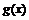 и
и 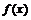 одного порядка при
одного порядка при  .
.
Определение 3.
Функция 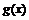 называется эквивалентной функции
называется эквивалентной функции 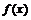 при
при  , если существует
, если существует 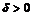 и функция
и функция 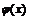 такие, что как только
такие, что как только 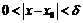 , выполняется
, выполняется 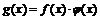 , причем
, причем  .
.
Для эквивалентности функций используется обозначение:
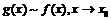 .
.
Аналогично определяется эквивалентность функций в случае 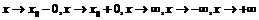 .
.
Вместо названия «эквивалентна» иногда пишут «асимптотически равна».
Непосредственно из определения следует, что отношение эквивалентности функций:
1) рефлексивно, то есть 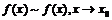 ;
;
2) симметрично, то есть, если 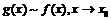 , то
, то 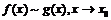 ;
;
3) транзитивно, то есть, если  , то
, то 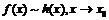 .
.
Теорема.
Для того чтобы функции 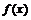 и
и 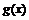 были эквивалентны при
были эквивалентны при  , достаточно, чтобы
, достаточно, чтобы 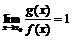 .
.
Из теоремы и известных пределов следуют часто применяемые эквивалентности: 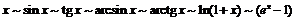 при
при  .
.
Справедливы и более общие эквивалентности: если при 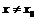 функция
функция 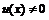 и при
и при 
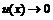 , то при
, то при 
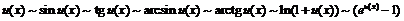 (следует из теоремы о пределе композиции).
(следует из теоремы о пределе композиции).
Пример 3. Какие из следующих пар функций являются эквивалентными при x→ 0:
1) 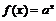 ,
, 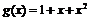 ;
;
2) 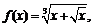
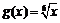 ;
;
3) 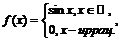
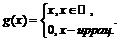
1) Так как 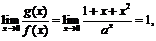 то
то 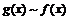 при
при  .
.
2) Так как 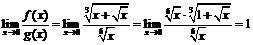 ,
,
то 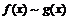 при
при  .
.
3) В этом случае 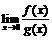 не существует, однако
не существует, однако 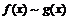 при x→ 0. Действительно, существует функция
при x→ 0. Действительно, существует функция 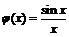 такая, что
такая, что 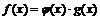 и
и 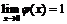 .
.
Теорема дает достаточное условие, но не необходимое. Это условие 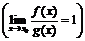 будет являться и необходимым, если в окрестности точки
будет являться и необходимым, если в окрестности точки 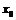
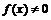 , и
, и 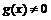 .
.
Определение 4.
Функция 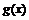 называется бесконечно малой по сравнению с функцией
называется бесконечно малой по сравнению с функцией 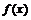 при
при  , если в некоторой проколотой окрестности точки
, если в некоторой проколотой окрестности точки 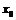 существует такая функция
существует такая функция 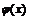 , что
, что 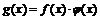 и
и 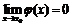 .
.
Из определения следует, что если в окрестности точки 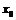
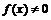 ,
, 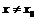 , то функция
, то функция 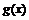 будет бесконечно малой по сравнению с
будет бесконечно малой по сравнению с 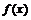 при
при  тогда и только тогда, когда
тогда и только тогда, когда 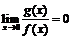 .
.
Для обозначения введенного понятия используется запись: 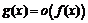 ,
,  (читается так: «
(читается так: «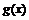 есть
есть 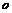 малое от
малое от 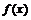 при
при  »). Аналогично определяется смысл записи
»). Аналогично определяется смысл записи 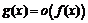 при
при 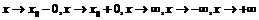 .
.
Если 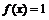 , то запись
, то запись 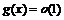 при
при  означает, что функция
означает, что функция 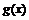 является бесконечно малой при
является бесконечно малой при  .
.
Определение 5.
Если при 
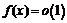 , а
, а 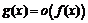 , то говорят, что функция
, то говорят, что функция 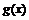 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 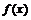 при
при  .
.
Пример 4. Установить, какие из следующих утверждений верны:
1) 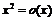 при а)
при а)  , б)
, б) 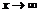 ;
; 
2) 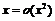 при а)
при а)  , б)
, б) 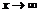 ;
;
3) 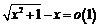 при а)
при а) 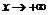 , б)
, б) 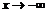 ;
;
4) 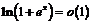 при а)
при а) 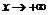 , б)
, б) 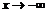 .
.
1) а) Утверждение верно, так как 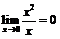 ;
;
б) Утверждение неверно, ибо 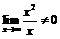 .
.
2) а) Утверждение неверно, так как 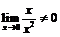 ;
;
б) Утверждение истинно, ибо 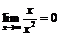 .
.
3) а) Утверждение верно, так как 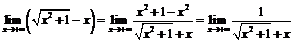
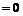 ;
;
б) Утверждение неверно, ибо 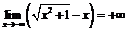 .
.
4) а) Утверждение неверно, так как  ;
;
б) Утверждение истинно, так как 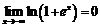 .
.
Пример 5. Доказать или опровергнуть утверждение: 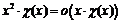 ,
,  , где
, где 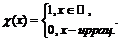
Здесь функция 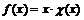 обращается в нуль в точках, сколь угодно близких к точке
обращается в нуль в точках, сколь угодно близких к точке 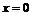 . Поэтому придется воспользоваться определением символа
. Поэтому придется воспользоваться определением символа  . Так как существует функция
. Так как существует функция 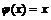 , что
, что  и
и 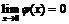 , то
, то 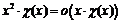 ,
,  - утверждение истинно.
- утверждение истинно.
Замечание!!
При использовании равенств с символами 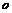 и
и 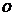 следует иметь в виду, что эти равенства не являются равенствами в обычном смысле. Так, из равенств
следует иметь в виду, что эти равенства не являются равенствами в обычном смысле. Так, из равенств 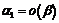 ,
, 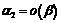 при
при  не следует, что
не следует, что 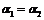 :
: 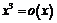 ,
, 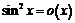 при
при  , но
, но  .
.
Пример 6. Докажем следующие правила: при  :
:
1) 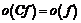 ,
,  — постоянная;
— постоянная;
2) 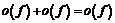 ;
;
3) 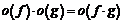 ;
;
4)  .
.
Для доказательства этих правил возьмем левую часть рассматриваемых равенств и докажем, что ее можно заменить правой.
1) По определению символа 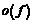 :
:
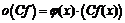 ,
, 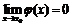 , но тогда
, но тогда
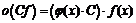 , где
, где 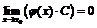 и
и 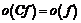 ,
,  .
.
2) Так как 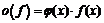 ,
, 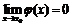 , то
, то 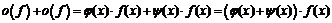 , где
, где 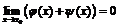 , и, таким образом,
, и, таким образом, 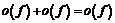 при
при  .
.
3) Учитывая, что 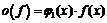 ,
, 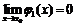 ,
, 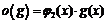 ,
, 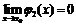 , получим:
, получим: 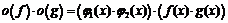 ,
,
где  , поэтому:
, поэтому: 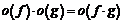 при
при  .
.
4) Так как 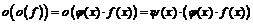 , где
, где 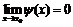 и
и 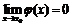 , то
, то 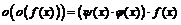 , где
, где 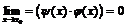 , т.е.
, т.е.  при
при  .
.
В силу доказанных соотношений 1) – 4) левую часть каждого из них можно заменить правой, проделать обратную замену, вообще говоря, нельзя.
Пример 7. Доказать равенства при  :
:
1) 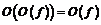 ;
;
2) 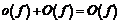 .
.
Обозначим 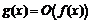 ,согласно определению символа
,согласно определению символа 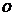 :
: 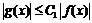 в некоторой
в некоторой 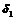 - окрестности точки
- окрестности точки 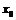 .
.
1) Тогда 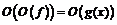 и, вводя обозначение
и, вводя обозначение 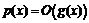 , будем иметь:
, будем иметь: 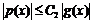 в некоторой
в некоторой
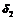 -окрестности точки
-окрестности точки 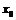 .
.
Если 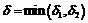 , то в
, то в 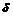 - окрестности точки
- окрестности точки 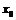 будем иметь
будем иметь 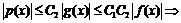
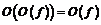 при
при  .
.
2) Символ 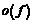 по определению означает:
по определению означает: 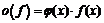 ,
, 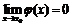 . Тогда
. Тогда 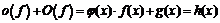 .
.
Так как 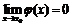 , то в некоторой окрестности точки
, то в некоторой окрестности точки 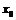
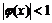 ,следовательно:
,следовательно: 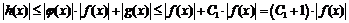 , то есть
, то есть 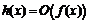 или
или 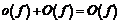 при
при  .
.
Вычисление пределов функций существенно упрощается, если использовать понятие эквивалентности функций и следующие две теоремы.
Теорема 1.
Для того чтобы функции 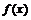 и
и 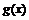 , отличные от нуля в некоторой окрестности точки
, отличные от нуля в некоторой окрестности точки 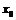 , были эквивалентными при
, были эквивалентными при  , необходимо и достаточно, чтобы выполнялось хотя бы одно из условий:
, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий: 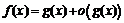 либо
либо 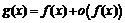 при
при  .
.
Теорема 2.
Пусть 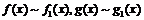 при
при  . Тогда, если существует
. Тогда, если существует 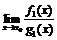 , то существует и
, то существует и  , причем эти пределы равны.
, причем эти пределы равны.
Пример 8.Найти 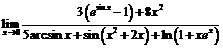 .
.
При  имеем:
имеем: 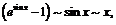
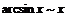 ,
, 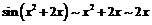 ,
, 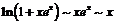 .
.
Следовательно, 
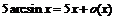 ,
,  ,
, 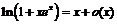 ,и
,и  Используя далее правила обращения с символами
Используя далее правила обращения с символами 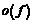 :
: 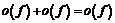 ,
, 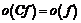
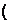 пример 6 (1,2)
пример 6 (1,2) 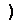 , получим:
, получим:
 .
.
Пример 9.Найти 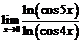 .
.
При  имеем:
имеем: 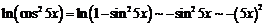 ,
,
аналогично 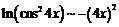 , поэтому
, поэтому 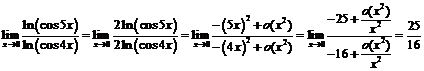 Пример 10. Найти
Пример 10. Найти 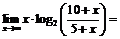
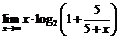 .
.
При 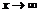 функция
функция 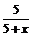
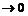 . Тогда, используя замечательный предел
. Тогда, используя замечательный предел 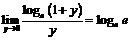 , получим:
, получим: 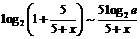 при
при 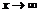 , т.е.
, т.е.  и
и 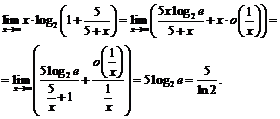
Убедимся, что 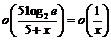 при
при 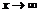 .
.
По определению символа 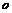 :
: 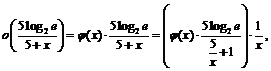 где
где 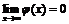 . Но тогда
. Но тогда 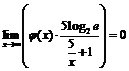 и требуемое установлено.
и требуемое установлено.
Пример 11.Найти 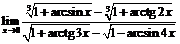 .
.
Воспользуемся замечательным пределом: 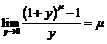 .
.
Тогда 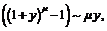
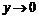 .
.
Поэтому 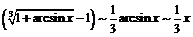 ,
, 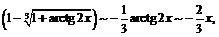
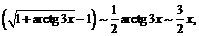
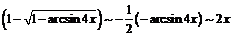 при
при  .
.
Следовательно, 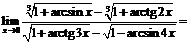
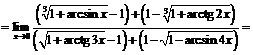
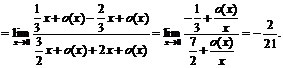
Определение 6.
Если функция 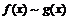 при
при  , то говорят, что функция
, то говорят, что функция 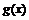 есть главная часть функции
есть главная часть функции 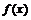 при
при  .
.
Например: 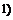
 при
при  , т.е.
, т.е. 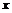 есть главная часть функции
есть главная часть функции 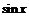 при
при  ;
;
2) 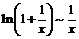 при
при 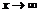 , т.е. функция
, т.е. функция 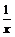 есть главная часть функции
есть главная часть функции 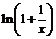 при
при 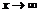 .
.
При решении задач удобно выразить главную часть б.м. или б.б. функции через простейшую б.м. или б.б.
Определение 7.
При  б.м. вида
б.м. вида  называют простейшей б.м., а б.б.
называют простейшей б.м., а б.б. 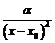 - простейшей б.б. При
- простейшей б.б. При 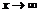 б.м.
б.м. 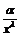 называют простейшей б.м., а б.б.
называют простейшей б.м., а б.б. 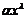 -простейшей б.б. (Здесь
-простейшей б.б. (Здесь 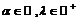 ).
).
Определение 8.
Нахождение для данной функции 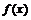 эквивалентной ей при
эквивалентной ей при  простейшей б.м. или б.б. называется выделением главной части функции при
простейшей б.м. или б.б. называется выделением главной части функции при  .
.
Пример 12. Выделить главную часть следующих б.м. или б.б. при  функций:
функций:
1) 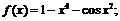 2)
2) 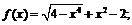
3) 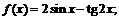 4)
4) 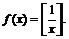
1) Так как 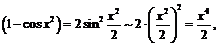 то
то
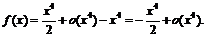
Итак, 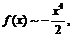
 .
. 
2) Так как 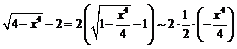 при
при  , то
, то 
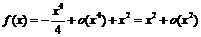 , следовательно,
, следовательно, 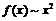 при
при  .
.
3) Требуется найти функцию вида 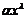 такую, что
такую, что  . Рассмотрим
. Рассмотрим 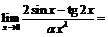
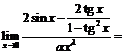
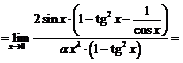
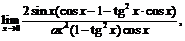
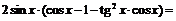
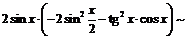 ~
~ 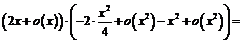
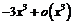 - согласно правилам обращения с символом
- согласно правилам обращения с символом 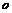 .
.
Тогда 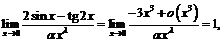 если
если 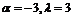 . Следовательно,
. Следовательно, 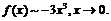
4) Функция