Определение предела функции по Коши

Предел функции

Будем рассматривать общий случай: векторную функцию векторного аргумента: 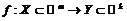или .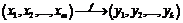

Существует два определения предела функции:

-по Гейне (на языке последовательностей);

-по Коши (на языке «ε-δ»-окрестностей).

Определение предела функции по Гейне:

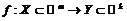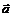Пусть и - предельная точка множества 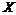. Вектор 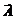называется пределом функции при , если для любой последовательности 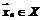, , 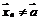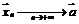соответствующая последовательность значений функции 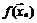всякий раз сходится к .

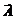Для предела используют обозначение: .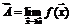

Определение сохраняет смысл для числовой функции, если 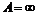, и для числовой функции числового аргумента, когда .

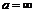Определив предел функции через предел последовательности, мы можем использовать все теоремы, касающиеся предела последовательности.

Пример 1. Покажем, что 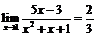. Для любой последовательности 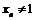, 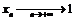по теореме об арифметических свойствах предела последовательности имеем:

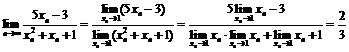
Определением предела функции по Гейне очень удобно пользоваться при доказательстве отсутствия предела функции.

Чтобы доказать, что 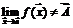, достаточно указать хотя бы одну последовательность 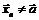, 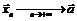и такую, что .

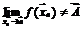Пример 2. Докажем, что 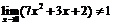. Пусть 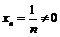, 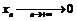. Тогда

.

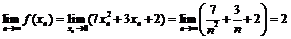Если же потребуется доказать, что 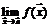не существует, то необходимо выбрать две различные последовательности 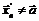, , 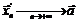, 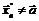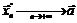и такие, что .

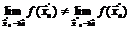Пример 3.Покажем, что не существует .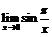

Выберем 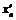и 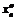из условий:

,

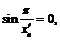
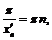
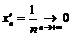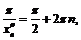
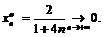
При этом .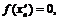

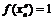Пример 4. Покажем, что функция Дирихле 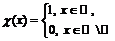не имеет предела ни в одной точке .

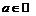Пусть 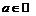- произвольно, а 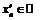, , 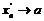тогда 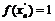, 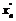-последовательность иррациональных чисел, 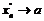, тогда 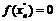. Таким образом, .

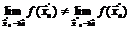Определение предела функции по Коши

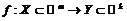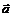Пусть и - предельная точка множества 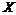. Вектор 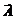называется пределом функци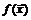и при 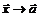, если для любой окрестности 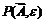вектора 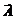существует такая проколотая окрестность 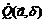точки 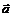, что как только 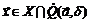, тотчас .

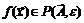Используя понятие окрестности, данное определение может быть сформулировано в следующем виде:

Вектор 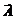называется пределом функци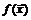и при 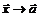, если для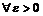 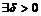такое, что для 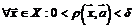тотчас выполняется .

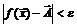Пример 5.Доказать, что .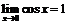

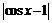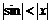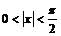Согласно определению оценим разность . Получим, используя неравенство для : , что 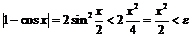, откуда 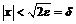. Таким образом, для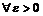 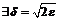такое, что для .

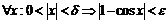Отметим, что и в рассмотренном примере, и во многих других мы не решаем неравенство 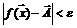, т.е. не находим множество тех и только тех значений 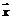, для которых оно имеет место. Наша цель – установить такую окрестность точки 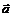, в которой неравенство заведомо выполняется.

Пример 6. Доказать, что .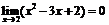

Оценим разность 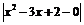. Имеем: 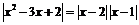. Множитель 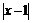не является ограниченным на множестве 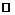, поэтому здесь необходимо выделить некоторую окрестность точки 2, в которой и проводить дальнейшие оценки, например, 1-окрестность, т.е. интервал (1,3). Для 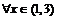имеем 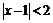, следовательно, 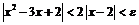. Так как 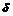- окрестность не должна выходить за пределы 1-окрестности, то положим 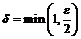, тогда из неравенства 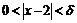будет следовать .

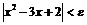Пример 7. Доказать, что .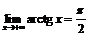

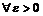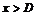Требуется для указать такое число , что для любого будет выполнено 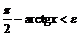, следовательно 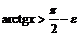. В силу монотонности функции 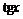на интервале 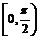получим: .

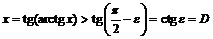Итак, для 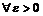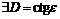, что .

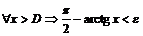Пример 8. Доказать, что .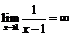

Требуется для 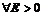указать 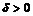такое, что при .

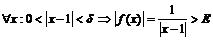Из последнего неравенства находим:

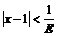, откуда получаем .

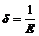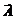Запишем на языке « » утверждение «вектор не является пределом функци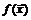и при »: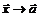

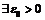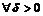
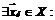
такое, чт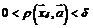о , но .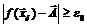

Пример 9. Покажем, что .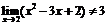

Рассмотрим разность

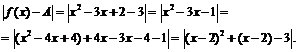
Используя неравенство 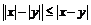, получим:

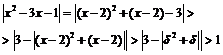
как только 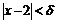для любого .

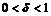Итак, 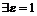, что при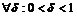 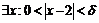, но при этом .

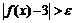Пример 10.Доказать, что не существует .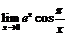

Пусть 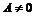- произвольное вещественное число.

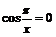, если .

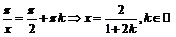Тогда, для ,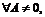

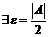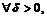
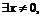
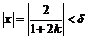
(за счёт выбора соответствующего целого числа 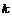), но тем не менее 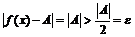. Следовательно, для .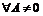

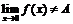Пусть теперь .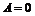

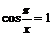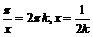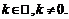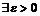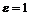
, если , В этом случае, , , 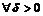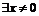и , что 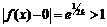. Итак, .

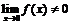Доказаны важные теоремы:

1. Определения Гейне и Коши эквивалентны.

2. Если существует предел 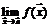, то этот предел единственный.

Отметим важный факт: в определениях предела по Гейне и Коши не требуется, чтобы функция 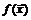была бы определена в точке 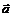, поэтому ни значение 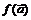, если 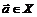, ни неопределённость 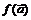не влияют на существование и величину .

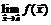Для числовой функции числового аргумента и векторной функции числового аргумента введём понятие одностороннего предела функции в данной точке .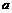

Определение Гейне:

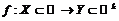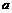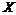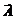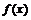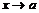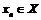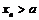
Пусть и - предельная точка множества . Вектор называется пределом функции при справа (слева), если для любой последовательности , , 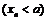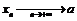соответствующая последовательность значений функции 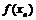всякий раз сходится к .

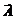Определение Коши:

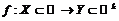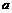Пусть и - предельная точка множества 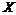. Вектор 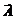называется пределом функци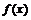и при 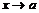справа (слева), если для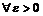 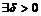такое, что для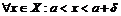 справедливо неравенство .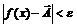

Для обозначения левого и правого пределов используют следующую символику:

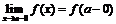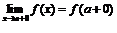, , есл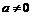и , и 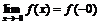, , 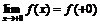если .

Теорема:

Функция 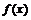имеет предел в точке 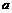тогда, и только тогда, когда существуют предел слева и предел справа и они равны: .

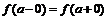Пример 11. Доказать, что 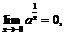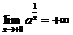, если .

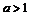При 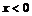неравенство 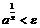справедливо для любого 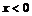, если 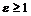, поэтому для 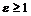в качестве 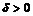подойдёт любое положительное число. Если же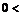 , то логарифмируя неравенство, получим: 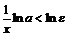, откуда 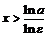. Таким образом, для 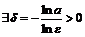такое, что для 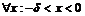имеет место: 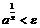, т.е. .

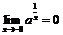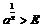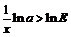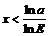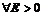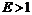
Рассмотрим неравенство: . Логарифмируя, имеем: , откуда . Следовательно, для , 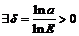такое, что для любого 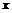: 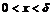тотчас выполняется: 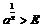, т.е. .

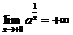Приведённые выше примеры показывают, что, пользуясь только определением предела, мы можем лишь проверить, является ли данное число пределом данной функции или нет, но не имеем конструктивного метода вычисления предела.