Математика
Способы выражения комплексных чисел
В ряде случаев квадратные уравнения не имеют решения в множестве действительных чисел. Например, для уравнения 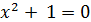 нельзя указать действительное значение неизвестного
нельзя указать действительное значение неизвестного 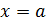 , удовлетворяющего его решению, поскольку
, удовлетворяющего его решению, поскольку 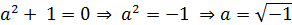 . Для решения аналогичных уравнений введен символ
. Для решения аналогичных уравнений введен символ 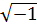 , который обозначается через j.
, который обозначается через j.
Комплексным числом  называется выражение вида
называется выражение вида 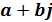 , где
, где 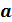 и
и 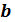 – действительные числа, символ
– действительные числа, символ  .
.
Комплексные числа имеют геометрическую интерпретацию. Для этого служит комплексная плоскость, имеющая две взаимно перпендикулярных оси; по горизонтальной оси откладывается действительная часть комплексного числа, по вертикальной оси – мнимая. Тогда комплексному числу на комплексной плоскости соответствует единственная определенная точка. Так комплексному числу  соответствует точка с координатами
соответствует точка с координатами 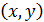 , при этом
, при этом  ; рисунок 5. Поэтому это же комплексное число можно записать в виде
; рисунок 5. Поэтому это же комплексное число можно записать в виде 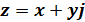 . Такая форма записи комплексного числа называется алгебраической.
. Такая форма записи комплексного числа называется алгебраической.
Рисунок 8 Рисунок 9
Между множеством комплексных чисел и множеством точек плоскости существует взаимно-однозначное соответствие.
Комплексные числа 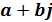 и
и 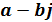 называются комплексно-сопряженными. Число, комплексно сопряженное числу
называются комплексно-сопряженными. Число, комплексно сопряженное числу  , обозначается
, обозначается 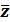 .
.
Если  , то его комплексно сопряженное число имеет вид
, то его комплексно сопряженное число имеет вид 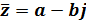 ; рисунок 9.
; рисунок 9.
Положение любой произвольной точки М на координатной плоскости можно задать двумя иными параметрами: r -длиной отрезка ОМ и φ -углом, образованным отрезком ОМ с осью ОР в положительном направлении; рисунок 10.
Рисунок 10
Совокупность точки О и оси ОР образует систему координат на плоскости, которая называется полярной системой. Числа r и φ называются полярными координатами точки М. При этом r называется полярным радиусом (модулем) точки М, φ - полярным углом (аргументом).
Для удобства работы с комплексными числами целесообразно совместить полярную и прямоугольную системы координат таким образом, чтобы полюс О совпадал с началом прямоугольной системы, а полярная ось ОР – с положительным направлением оси x; рисунок 11.
Рисунок 11
Точка М в полярной системе имеет координаты r и φ, в прямоугольной системе – x и y. Из рисунка 11 очевидно, что эти координаты связаны соотношениями:
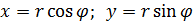 ; (1)
; (1)
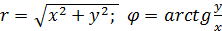 .(2)
.(2)
При определении угла φ необходимо учитывать знаки переменных x и y.
Если точка М представляет некое комплексное число 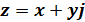 (3), то числа x и y являются ее координатами в прямоугольной системе. Подставив уравнения (1) в уравнение (3) получаем тригонометрическую форму записи комплексного числа:
(3), то числа x и y являются ее координатами в прямоугольной системе. Подставив уравнения (1) в уравнение (3) получаем тригонометрическую форму записи комплексного числа:
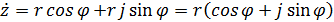 ,
,
где  . - мнимая часть комплексного числа,
. - мнимая часть комплексного числа,
 - действительная часть.
- действительная часть.
В полярной системе точка М имеет координаты r и φ, где r – абсолютная величина комплексного числа (модуль), φ – аргумент комплексного числа (полярный угол).
Формулы (1) служат для перевода тригонометрической формы комплексного числа в алгебраическую; формулы (2) – для перевода алгебраической формы комплексного числа в тригонометрическую.
Комплексное число может быть представлено в показательной форме, для чего используется формула Эйлера:
 .
.
Если мнимая часть комплексного числа в алгебраической форме имеет знак минус, то аргумент этого числа в показательной форме также имеет знак минус:
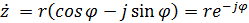 .
.