Изокванта означает одинаковое количество продукции, т.е. изокванте принадлежат любые комбинации труда и капитала, которые позволяют фирме производить то же самое количество продукции.
При фиксированном Q производственной функции Q = f(L, K) соответствует определенная изокванта.
Изокванта – это «кривая безразличия» для производственной функции. Семейство изоквант показано на рисунке:
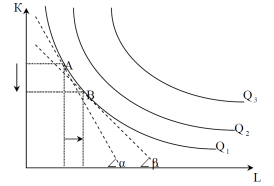
Важнейшая характеристика изокванты – предельная норма технического замещения или MRTS.
Если отложить труд (L) по горизонтали, капитал (К) по вертикали, то

Здесь Q – фиксированный выпуск продукции.
MRTSLK по своему экономическому содержанию, аналогична MRS XY, рассматриваемой в теории потребительского выбора.
MRTSLK – это норма, в которой количество капитала может быть уменьшено при увеличении количества труда на 1 единицу, при этом выпуск продукции остается неизменным.
MRTSLK можно также определить как норму, в которой количество капитала может быть увеличено при уменьшении количества труда на 1 единицу при неизменности объема выпускаемой продукции.
Поскольку при движении вдоль изокванты количество произведенной продукции не меняется, то справедливо равенство:
ΔL·MPL + ΔK·МР K = ΔQ = 0.
Отсюда,
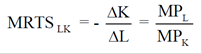
Геометрически MRTSLK равна тангенсу угла наклона касательной, например MRTSLK (А) = tgα, MRTS LK (B) = tgβ (рис.).
При движении вдоль изокванты сверху вниз MRTSLK убывает, или, что эквивалентно, изокванта является выпуклой к началу координат. Убывание предельной нормы технического замещения связано с законом убывающей предельной отдачи, т.к. именно этот закон определяет изменение величин MPL и МРK при изменении L и К.
Задача 1
Фирма использует два ресурса в количествах x1 и x2; ее производственная функция q = a  , цены ресурсов p1 и p2. Найти:
, цены ресурсов p1 и p2. Найти:
а) уравнение пути оптимального роста фирмы;
б) функцию общих затрат длительного периода;
в) функцию общих затрат короткого периода, считая первый ресурс переменным, второй – постоянным.
Решение:
а) Путь оптимального роста фирмы – это множество экономически эффективных способов производства, т. е. таких способов, которые позволяют произвести любое возможное количество продукта с минимальной стоимостью используемых ресурсов. Для каждого экономически эффективного способа предельная норма технического замещения ресурсов равна соотношению их цен.
Предельные производительности ресурсов:

предельная норма технической замены:

Таким образом, путь оптимального роста — прямая, описываемая уравнением:

б) Используем полученное уравнение для определения экономически эффективного набора ресурсов, необходимого для производства продукта в количестве q. Подставим выражение для x2 в производственную функцию:

откуда

в) В случае, когда x2 = const, изменение объема выпуска достигается выбором соответствующей величины x1, так что в коротком периоде

и поэтому

Комментарий. Поскольку LTC(q) — это минимальные затраты на производство объема q при условии, что все ресурсы — переменные, а STC(q) – минимальные затраты при условии, что некоторые ресурсы — постоянные, можно утверждать, что STC(q) ≥ LTC(q) при любом q. Выражения для затрат короткого и длительного периодов, полученные при решении задачи, иллюстрируют это общее положение:

Задача 2
Обнаружено, что при остановке автоматического станка происходит уменьшение выработки за день с 200 ед. прод. до 180 ед.прод. В случае невыхода на работу 10 сотрудников уменьшение объема производства составляет с 200 ед. прод. до 190 ед. прод. Сколько сотрудников можно сократить безболезненно для объема выпуска, если купить дополнительно 1 станок? Как этот показатель называется на языке экономической теории?
Решение:
1. Предельный продукт:
МРст = (200-180) ед. прод. / 1 станок = 20 ед.пр./ст.
МРсотр = (200-190) сотр. / 10 сотр. = 1 ед.пр. /сотр.
Предельная норма технического замещения:
MRTSсотр/ст = МРст/МРсотр = 20/1 = 20 сотр/ст
Задача 3
На оптимальное соотношение факторов производства. Цена рабочей силы – 1000 руб. Цена работы единицы оборудования – 2000 руб.
Какой прирост производства продукции принесет найм трех дополнительных рабочих, если только что установленный станок привел к увеличению объема производства на 100 ед. прод., считая, что структура производства оптимальна.
Решение:
В точке оптимума МР раб/ МР обор = Рраб/ Робор
МРобор = 100 ед.пр./ст.
МРраб. = (Рраб. / Робор.) ·МР обор. = (1000 р./чел. /2000 р./чел.)*100 ед.пр./ст. = 50 ед.пр./чел.
Δf = МР раб. * ΔХраб = 50 ед.пр./чел. * 3 чел. = 150 ед.пр.
Задача 4
Построить производственную функцию методом изоквант, найти линию оптимального производства (графически) при ценах факторов производства Рх1 = 2 р./шт., Рх2 = 4 р,/шт. Производственная функция:
F(x1,x2) =  =
= 

Решение:
При f = 1 линия изокванты х1 = 1/х2. Функция строится по точкам при f = 2 линия изокванты х1 = 4/х2. В точке равновесия d x2/ d x1 = Px1/ Px2 = 2/4 = 1/2.
Для f1 точка равновесия
x2’ = (1/x1)’ = - 1/x12 = - 1/2
0,7 1 1, 4 2 3 4 х2
x1 = √2 x2 = 1/ √2
Решение аналогично задачи 1:
а) Путь оптимального роста фирмы – это множество экономически эффективных способов производства, т. е. таких способов, которые позволяют произвести любое возможное количество продукта с минимальной стоимостью используемых ресурсов. Для каждого экономически эффективного способа предельная норма технического замещения ресурсов равна соотношению их цен.
Предельные производительности ресурсов:

предельная норма технической замены:

Таким образом, путь оптимального роста — прямая, описываемая уравнением:
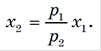
б) Используем полученное уравнение для определения экономически эффективного набора ресурсов, необходимого для производства продукта в количестве q. Подставим выражение для x2 в производственную функцию:

откуда


Эластичность замещения
Эластичность замещения (σ) измеряет, как быстро предельная норма технического замещения капитала трудом (MRTS LK) изменяется при движении вдоль изокванты.
При движении вдоль изокванты сверху вниз изменяется соотношение (K/L), причем оно падает. Поэтому можно найти процентное изменение в соотношении (K/L), приходящееся на каждый процент изменения величины MRTS LK при движении вдоль изокванты.
Эластичность замещения (σ), таким образом, может быть рассчитана по формуле:

Очевидно, σ ≥ 0.
Если замещение капитала трудом осуществляется трудно (с технической точки зрения), тогда процентное изменение в MRTS LK при движении вдоль изокванты будет значительным и величина σ будет близка к нулю.
Если замещение капитала трудом осуществляется легко, то процентное изменение в MRTSLK будет незначительным и величина σ будет большой.
Можно сказать, что коэффициент σ определяет меру кривизны изокванты.

На рис (а) фирма имеет ограниченные возможности замещения капитала трудом, MRTSLK изменяется заметно при движении вдоль изокванты; изокванта имеет L – образную форму.
На рис. (б) фирма обладает широкими возможностями для замещения одного фактора производства другим, MRTS LK изменяется незначительно при движении вдоль изокванты.
Задача 1
Задана производственная функция Q = √L + √K. Чему равна эластичность замещения труда капиталом?
Решение:
Найдем MRTS LK.
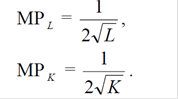
Запишем значение σ следующим образом:

Обратите внимание, что отношение K/L рассматривается как функция от величины MRTSLK. Если ввести упрощающие обозначения MRTS LK = х,
K/L = у, то у = х 2 и


Следовательно,

Задача № 2
Найти эластичности замещения ресурсов для следующих производственных функций:

Решение:
Эластичность замещения ресурсов представляет собой эластичность отношения количеств ресурсов x2/x1 по предельной норме технической замены MRTS12.
а) Найдем предельные продукты ресурсов:

Отсюда

Предельная норма технической замены представляет собой степенную функцию отношения x2/x1; показатель степени равен 1/2. Эластичность степенной функции равна показателю степени, так что эластичность MRTS12 по x2/x1 равна 1/2, а эластичность обратной зависимости, которая нас интересует, равна 2.

В этом случае зависимость также степенная, показатель степени равен 1; соответственно эластичность замещения равна 1.

Здесь показатель степени равен 2, эластичность замещения равна 1/2.