Производство и производственная функция
Производство – это деятельность, направленная на преобразование экономических ресурсов (факторов производства) в целях получения необходимых экономическим субъектам товаров и услуг.
Системы производства:
1. Заказное (или штучное) – предполагает производство по индивидуальным заказам и завершается выпуском единственного в своем роде, уникального продукта (произведение искусства, самолет, здание офиса или электростанция и т.п.)
Главная особенность – высокая эффективность даже при малых масштабах, спрос на высококвалифицированные ресурсы (их количество – основной фактор определяющий размеры производства).
2. Массовое – производство большими или небольшими партиями многих видов изделий из однотипных и стандартизованных комплектующих:
а) негибкое – выпуск однородной стандартизованной продукции; капиталоемкая технология, которая достигает результатов при больших объемах выпуска (фраза Генри Форда: «Потребитель может пожелать машину любого цвета, если этот цвет черный»);
б) гибкое – производство с расширением номенклатуры изделий, использованием различных комбинаций стандартных комплектующих (производство автомобилей различных моделей на основе использования одних и тех же двигателей).
в) поточное (процессное) – характеризуется непрерывным потреблением сырья и материалов и соответственно непрерывным потоком продукции. Например, нефтеперерабатывающие заводы, заводы по промышленной переработки молока и т. п. Наибольшая эффективность достигается при круглосуточной работе 7 дней в неделю, т.к. чем выше степень использования оборудования, тем ниже себестоимость. Высокоавтоматизированное и капиталоемкое производство, требующее малого использования трудовых ресурсов.
Технология производства – способ соединения экономических ресурсов для производства заданного объема товаров и услуг. Критерием выбора той или иной технологии является эффективность производства, различают:
1. Экономическую эффективность, которая отражает стоимостную зависимость между расходами фирмы на факторы производства (издержками) и ее доходами.
2. Технологическую эффективность, которая характеризует зависимость между используемыми ресурсами и получаемой продукцией в натуральном выражении, которая оценивается:
1) через максимизацию выпуска при данной комбинации ресурсов;
2) через минимизацию количества ресурсов, обеспечивающих данный объем выпуска.
Изменение цен или каких-либо других параметров рыночной конъюнктуры может сделать ранее выбранный способ производства неэффективным, и наоборот.
Технологическая зависимость между количеством ресурсов, затрачиваемых в единицу времени, и максимально возможным объемом выпуска продукции называют производственной функцией.
Производственные ресурсы, такие как рабочая сила, капитал, используемые фирмой для производства товаров и услуг, называются факторами производства. Фирма может использовать различные комбинации факторов для производства заданного объема продукции.
Производственная функция есть математическое представление различных технологических способов, из которых фирма может выбирать для производства продукции.
Производственная функция характеризует максимальный выпуск продукции при заданных количествах используемых факторов производства.
Для двух факторов производства – рабочей силы (труда, L) и капитала (К) – производственную функцию можно записать следующим образом:
Q = f(L, K).
Покажем на графике в общем виде производственную функцию, если фирма использует только один ресурс – труд.
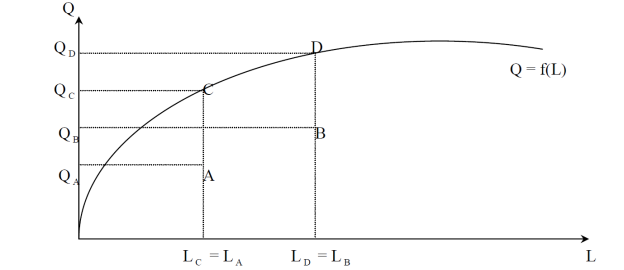
В точках С и D фирма использует технически эффективные способы производства, т.к. она производит максимально возможное количество продукции при заданном количестве труда.
В точках А и В фирма работает технически неэффективно, т.к. она не получает максимально возможное количество продукции.
Зная функцию Q = f(L), можно найти обратную функцию L = g(Q), которая характеризует минимальное количество труда, необходимое для производства выпуска Q.
Производственные функции, зависящие от одного производственного фактора (например, труда), называют функциями общего выпуска – ТР или общего продукта, т.е. Q = f(L) = TP L, Q = φ(K) = TP K и т.п.
Главными характеристиками производственной функции Q = f(L) являются средний (АР L) и предельный (МР L) продукт:

Аналогично:  и т.п.
и т.п.
Взаимосвязь общего, среднего и предельного продукта какого-либо фактора производства определяется действием закона убывающей предельной отдачи фактора производства.
Согласно этому закону, если используемое количество какого-либо ресурса (например, труда) увеличивается при неизменных количествах других ресурсов (капитала, земли), то с определенного момента предельная отдача этого ресурса начнет сокращаться.
С учетом действия закона убывающей отдачи для производственной функции одной переменной Q = f(L) кривые TP L, АP L и МP L показаны на рисунке:
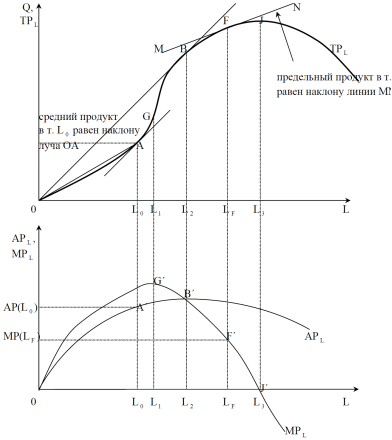
Предельный продукт труда в любой точке измеряется наклоном касательной (тангенсом угла наклона) к линии TP L. Средний продукт труда измеряется наклоном луча, проведенного из начала координат к соответствующей точке графика TP L.
На рисунке кривая TP L имеет так называемую S-образную форму, что объясняется переходом от возрастающей предельной отдачи труда (на участке 0 ≤ L ≤ L1) к убывающей предельной отдаче (на участке L > L1).
Вначале вовлечение в производство дополнительной единицы труда приводит к росту предельного продукта, но, начиная с некоторого момента (на рис. это L = L1 ), предельная отдача труда снижается. Таким образом, можно выделить 3 сегмента в изменении предельного продукта:
1. МP L возрастает (0 ≤ L ≤ L1);
2. МP L уменьшается, но при этом МP L > 0 (L1 < L < L 3);
3. МP L уменьшается, но при этом МP L < 0 (L > L 3).
В т. L = L1 функция МP L достигает своего максимума. Соответственно кривая ТP L, оставаясь возрастающей, в т. L = L1 меняет свою кривизну. При L = L3 МP L = 0, следовательно, значение ТP L достигает своего максимума.
При выборе способа производства фирма должна учитывать изменение не только предельного продукта, но и изменение среднего продукта. По характеру взаимосвязи среднего и предельного продуктов выделяют 3 стадии производства:
1. МP L > AP L, функция AP L возрастает; на рисунке этой стадии соответствует участок 0 ≤ L ≤ L 2;
2. МP L < AP L, функция AP L убывает, но при этом МP L > 0; на рисунке этой стадии соответствует участок L 2 < L < L 3;
3. МP L < AP L, функция AP L убывает, но при этом МP L < 0; на рисунке этой стадии соответствует участок L > L 3.
Очевидно, фирме выходить за пределы 2-й стадии не имеет экономического смысла.
Очевидно также, что в т. L = L 2 средний продукт достигает своего максимального значения.
Таким образом, кривые среднего и предельного продукта пересекаются в точке максимума среднего продукта. Математически это положение можно доказать, найдя производную среднего продукта и приравняв ее нулю.

Задача 1
Технология производства предполагает использование двух ресурсов и характеризуется постоянной отдачей от масштаба. Производство 60 единиц продукта требует затрат ресурсов в количествах x1 = 12 и x2 = 4. Предельный продукт первого ресурса MP1 = 3. Чему равен предельный продукт второго ресурса?
Решение:
Производственная функция q = f(x1, x2) c постоянной отдачей от масштаба обладает следующим свойством: при любом положительном k выполняется равенство f(kx1, kx2) = kf(x1, x2).
Почленно дифференцируя это равенство по k, получим:

или MP1 ∙ x1 + MP2 ∙ x2 = q, откуда MP2 = (q – MP1 ∙ x1)/x2. При данных задачи находим: MP2 = (60 – 3 ∙ 12)/4 = 6.