Производственные ресурсы, такие как рабочая сила, капитал, используемые фирмой для производства товаров и услуг, называются факторами производства. Фирма может использовать различные комбинации факторов для производства заданного объема продукции.
Производственная функция есть математическое представление различных технологических способов, из которых фирма может выбирать для производства продукции.
Производственная функция характеризует максимальный выпуск продукции при заданных количествах используемых факторов производства.
Для двух факторов производства – рабочей силы (труда, L) и капитала (К) – производственную функцию можно записать следующим образом:
Q = f(L, K).
Покажем на графике в общем виде производственную функцию, если фирма использует только один ресурс – труд.
В точках С и D фирма использует технически эффективные способы производства, т.к. она производит максимально возможное количество продукции при заданном количестве труда.
В точках А и В фирма работает технически неэффективно, т.к. она не получает максимально возможное количество продукции.
Зная функцию Q = f(L), можно найти обратную функцию L = g(Q), которая характеризует минимальное количество труда, необходимое для производства выпуска Q.
Производственные функции, зависящие от одного производственного фактора (например, труда), называют функциями общего выпуска – ТР или общего продукта, т.е. Q = f(L) = TP L, Q = φ(K) = TP K и т.п.
Главными характеристиками производственной функции Q = f(L) являются средний (АР L) и предельный (МР L) продукт:
Аналогично: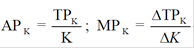 
и т.п.
Взаимосвязь общего, среднего и предельного продукта какого-либо фактора производства определяется действием закона убывающей предельной отдачи фактора производства.
|
|
Согласно этому закону, если используемое количество какого-либо ресурса (например, труда) увеличивается при неизменных количествах других ресурсов (капитала, земли), то с определенного момента предельная отдача этого ресурса начнет сокращаться.
С учетом действия закона убывающей отдачи для производственной функции одной переменной Q = f(L) кривые TP L, АP L и МP L показаны на рисунке:
Предельный продукт труда в любой точке измеряется наклоном касательной (тангенсом угла наклона) к линии TP L. Средний продукт труда измеряется наклоном луча, проведенного из начала координат к соответствующей точке графика TP L.
На рисунке кривая TP L имеет так называемую S-образную форму, что объясняется переходом от возрастающей предельной отдачи труда (на участке 0 ≤ L ≤ L1) к убывающей предельной отдаче (на участке L > L1).
Вначале вовлечение в производство дополнительной единицы труда приводит к росту предельного продукта, но, начиная с некоторого момента (на рис. это L = L1 ), предельная отдача труда снижается. Таким образом, можно выделить 3 сегмента в изменении предельного продукта:
1. МP L возрастает (0 ≤ L ≤ L1);
2. МP L уменьшается, но при этом МP L > 0 (L1 < L < L 3);
3. МP L уменьшается, но при этом МP L < 0 (L > L 3).
В т. L = L1 функция МP L достигает своего максимума. Соответственно кривая ТP L, оставаясь возрастающей, в т. L = L1 меняет свою кривизну. При L = L3 МP L = 0, следовательно, значение ТP L достигает своего максимума.
При выборе способа производства фирма должна учитывать изменение не только предельного продукта, но и изменение среднего продукта. По характеру взаимосвязи среднего и предельного продуктов выделяют 3 стадии производства:
|
|
1. МP L > AP L, функция AP L возрастает; на рисунке этой стадии соответствует участок 0 ≤ L ≤ L 2;
2. МP L < AP L, функция AP L убывает, но при этом МP L > 0; на рисунке этой стадии соответствует участок L 2 < L < L 3;
3. МP L < AP L, функция AP L убывает, но при этом МP L < 0; на рисунке этой стадии соответствует участок L > L 3.
Очевидно, фирме выходить за пределы 2-й стадии не имеет экономического смысла.
Очевидно также, что в т. L = L 2 средний продукт достигает своего максимального значения.
Таким образом, кривые среднего и предельного продукта пересекаются в точке максимума среднего продукта. Математически это положение можно доказать, найдя производную среднего продукта и приравняв ее нулю.
Задача 1
Технология производства предполагает использование двух ресурсов и характеризуется постоянной отдачей от масштаба. Производство 60 единиц продукта требует затрат ресурсов в количествах x1 = 12 и x2 = 4. Предельный продукт первого ресурса MP1 = 3. Чему равен предельный продукт второго ресурса?
или MP1 ∙ x1 + MP2 ∙ x2 = q, откуда MP2 = (q – MP1 ∙ x1)/x2. При данных задачи находим: MP2 = (60 – 3 ∙ 12)/4 = 6.