Математика «Алгебра и начала математического анализа»
Раздел: Комбинаторика
Тема: Правило суммы, правило произведения
Составитель:
Курганова О.Р.
Преподаватель математики;
ГБПОУ «Озерский технический колледж»
Название темы по программе: Правило суммы, правило произведения
Практическое занятие № 71
Тема: Правило суммы, правило произведения
1. Цель занятия;
Изучение понятий комбинаторики: правила суммы и правила произведения, Наработка навыков решения комбинаторных задач с применением закона сложения и умножения.
2. Дидактическое оснащение практического занятия:
Теория по ссылке: Закон сложения в комбинаторике, Закон умножения в комбинаторике
| Закон сложения | Допустим, что есть две группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы какой-либо элемент можно выбрать k способами, а из второй n способами, то выбрать один элемент из первой или второй группы можно k + n способами. Закон сложения также используется, если нужно выбрать элемент из трёх, четырёх и т.д. групп. |
| Важно! | Закон сложения используется тогда, когда нужно выбрать только 1 элемент. |
| Правило использования закона сложения | Чтобы использовать закон сложения: 1. нужно понять, каковы группы, из которых нужно выбрать 1 элемент; 2. нужно выяснить количество элементов в каждой группе; 3. нужно убедиться, что в различных группах, из которых выбирают элемент, нет одинаковых элементов. |
| Важно! | Применение закона сложения невозможно, если есть совпадения при выборе элементов из групп |
| Если есть m — количество повторяющихся способов, то закон сложения (с повторениями) | Если объект a можно получить k способами, объект b n способами, то объект «a или b » можно получить k + n − m способами, где m — это количество повторяющихся способов. |
| Закон умножения | Если элемент A можно выбрать k способами и затем второй элемент B можно выбрать m различными способами, то пару элементов A и B можно выбрать k ⋅ m способами. Закон выполняется так же, если нужно выбирать по 1 элементу из трёх, четырёх и т.д. групп. |
Задания
Задание№1. Выбор элемента из нескольких групп
| Дана хочет нарядиться на классный вечер. В её шкатулке 5 цепочек, 3 колец и 12 браслетов. Сколькими способами она может выбрать одно украшение? | |
| Решение: Закон сложения: Существуют 2 группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы элемент можно выбрать k способами, а из второй — n способами, то выбрать элемент из первой или второй группы можно k + n способами. Закон также в силе, если дано большее количество групп. В данном задании 3 группы: цепочки, кольца и браслеты. Цепочку можно выбрать 5 способами; Кольцо можно выбрать 3 способами; Браслет можно выбрать 12 способами. Одно украшение можно выбрать 5+3+12=20 способами. Ответ:Одно украшение можно выбрать 5+3+12=20 способами. | |
| Решить задание на ЯКласс | №1 Выбор элемента из нескольких групп |
Задание №2 Выбор элемента из множества групп, выбор нужной группы
В школьном самоуправлении участвуют ученики разных классов.
Данные обобщены в таблице:
Сколькими способами можно выбрать одного ведущего школьного мероприятия, если для роли ведущего нужно выбрать девочку из 10-ого или 9-ого класса?
| |||||||||||||||
| Решение: Допустим, что существуют 2 группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы какой-либо элемент можно выбрать k способами, а из второй - n способами, то выбрать один элемент из первой или второй группы можно k + n способами. Закон сложения остаётся в силе, если групп больше, чем 2. В данном случае группы — это девочки из 10-ого и 11-ого класса, количество элементов - количество девочек в этих классах. Из закона сложения следует, что ведущего мероприятия можно выбрать 9+8=17 способами. Ответ: Одного ведущего можно выбрать 17 способами | |||||||||||||||
| Решить задание на ЯКласс | №2 Выбор элемента из множества групп, выбор нужной группы |
Задание №3 Варианты выбора элемента из нескольких групп
| По телевизору в воскресенье показывают 6 приключенческих фильмов, 5 комедий и 2 фильмов ужасов. Запиши, сколькими различными способами можно выбрать один из всех предложенных фильмов? | |
| Решение: Используется закон сложения: Если в двух группах нет одинаковых элементов и из одной группы какой —либо элемент можно выбрать n способами, а из второй — k способами, то выбрать один элемент из первой или второй группы можно n + k способами. 6+5+2=13 Ответ:Из всех фильмов один можно выбрать 13 различными способами. | |
| Решить задание на ЯКласс | №3 Варианты выбора элемента из нескольких групп |
Задание №4 Варианты маршрутов по данному рисунку
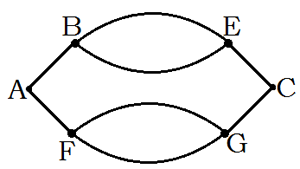
. Отметь, сколькими различными способами можно попасть из города A в город C, если на данном рисунке схематически изображены варианты путей?
| |
Решение:
Количество различных путей из города A в город C: 1⋅2⋅1+1⋅2⋅1=2+2=4
Объяснение:
Если ехать через города B и E, нужно выбрать комбинацию из 3 элементов: из A в B есть 1 возможность; из B в E есть 2 возможности; из E в C есть 1 возможность. По закону умножения из города A в C через B и E можно попасть 1⋅2⋅1=2 способами. Если ехать через города F и G, нужно выбрать комбинацию из 3 элементов: из A в F есть 1 возможность; из F в G есть 2 возможности; из G в C есть 1 возможность. По закону умножения из A в C через F и G можно попасть 1⋅2⋅1=2 способами. По закону сложения количество всех возможных путей равно
1⋅2⋅1+1⋅2⋅1=2+2=4
Ответ:количество всех возможных путей равно 4
| |
| Решить задание на ЯКласс | №4 Варианты маршрутов по данному рисунку |
Задание №5 Варианты выбора двух элементов (закон умножения)
| На полке лежит 8 пар брюк. Игорь для путешествия из них выбирает 2 пары. Выясни, сколькими различными способами Игорь может выбрать себе брюки? | |
Решение:
1. Сначала Игорь может выбрать любые из всех 8 брюк.
2. Когда первый выбор сделан, для следующего остаётся 8−1=7 вариантов брюк.
3. По закону умножения:
Если элемент A можно выбрать k способами и затем второй элемент B можно выбрать m различными способами, пару элементов A и B можно выбрать k ⋅ m способами.
8⋅7=56 (способами).
Ответ:Игорь может выбрать брюки 56 различными способами.
| |
| Решить задание на ЯКласс | № 5 Варианты выбора двух элементов |
Задание №6 Выбор по одному элементу из трех групп
| Дана корзина с конфетами разных видов. Из всех конфет 9 конфет «Буревестник», 11 конфет «Клубничные» и 3 конфеты «Белочка». Найди, сколькими способами можно выбрать 3 конфеты так, чтобы это были 1 «Буревестник», 1 «Клубничная» и 1 «Белочка»? | |
| Решение: О Для решения задачи используется закон умножения. Если элемент A можно выбрать k способами и затем другой элемент B независимо от выбора элемента A можно выбрать m различными способами, пару элементов A и B можно выбрать k ⋅ m различными способами. Закон в силе и тогда, когда нужно выбирать по одному элементу из большего количества групп. 9⋅11⋅3=297 Ответ:Конфеты можно выбрать 297 различными способами. | |
| Решить задание на ЯКласс | № 5 Выбор по одному элементу из трех групп |
Содержание отчета
Записать решение заданий в тетрадь, ответить на контрольные вопросы
5. Контрольные вопросы
| Какой закон применим для выбора 1 элемента из нескольких групп? | |
| Возможно ли применение закона сложения при выборе элементов из нескольких групп, если есть совпадения при выборе элементов?? | |
| Какой закон применяется при выборе нескольких элементов из одной или нескольких групп? | |
| В чем разница применения закона сложения и уможения? |
Литература и используемые интернет-ресурсы
| Образовательный портал ЯКласс www. yaklass.ru | |
| Учебник для учащихся общеобразовательных учреждений (базовый уровень). М.: Мнемозина, 2009. | |