Перечислим некоторые функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой.
1. C – константа
2. log(log(N))
3. log(N)
4. N^C, 0<C<1
5. N
6. N*log(N)
7. N^C, C>1
8. C^N, C>1
9. N!
Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!).
Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой можно считать сложность O(N^2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N).
Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью N^C можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями C^N и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объёма данных.
В заключение приведём таблицу, которая показывает, как долго компьютер, осуществляющий миллион операций в секунду, будет выполнять некоторые медленные алгоритмы.
Каждый алгоритм в зависимости от реализации имеет определенную сложность вычисления. Чаще всего под сложностью вычисления понимают количество времени необходимое алгоритму для решения задачи. В настоящее время принято использовать следующие виды оценок сложности вычисления (Классы сложности):
| № п.п.(От сложного к простому) | Название сложности | Мат. формула | Примеры алгоритмов |
| Факториальная | N! | Алгоритмы комбинаторики (сочетания, перестановки и т.д.) | |
| Экспоненциальная | KN | Алгоритмы перебора (brute force) | |
| Полиномиальная | NK | Алгоритмы простой сортировки (buble sort) | |
| Линейный логарифм | N * log(N) | Алгоритмы быстрой сортировки (heap sort) | |
| Линейная | K * N | Перебор элементов массива | |
| Логарифмическая | K * log(N) | Бинарный поиск | |
| Константная | К | Обращение к элементу массива по индексу |
Задача оценки сложности алгоритма заключается в анализе сложности вычисления для разных наборов входных данных (разный объем, порядок и т.д.). Для каждого алгоритма перед началом его реализации необходимо получить следующие виды оценок:
1. Наилучшая сложность вычисления.
2. Средняя сложность вычисления.
3. Наихудшая сложность вычисления.
ASCII - таблица была разработана и стандартизована в США, в 1963 году.
Три правила оценки сложности.
1. O (k*f) = O (f),
2. O (f*g) = O (f)* O (g),
3. O (f+g) = Max ( O (f), O (g)).
Здесь k обозначает константу, а f и g - функции.
Первое правило означает, что постоянные множители не имеют значения для определения порядка сложности, например, O ( 2 *n) = O (n). В соответствии со вторым порядок сложности произведения двух функций равен произведению их сложностей. Например, O (( 10 *n)* n) = O (n)* O (n) = O (n2). На основании третьего правила порядок сложности суммы двух функций равен максимальному (доминирующему) значению из их сложностей. Например, O (n4 + n2) = O (n4).
На практике применяются следующие виды О-функций:
a) О(1) – константная сложность, для алгоритмов, сложность которых не зависит от размера данных.
b) О (n) – линейная сложность, для одномерных массивов и циклов, которые выполняются n раз,
c) О (n2), О (n3), … – полиномиальная сложность, для многомерных массивов и вложенных циклов, каждый из которых выполняется n раз,
d) О (log(n)) – логарифмическая сложность, для программ, в которых большая задача делится на мелкие, которые решаются по-отдельности,
e) О ( 2 n) – экспоненциальная сложность, для очень сложных алгоритмов, использующих полный перебор или так называемый «метод грубой силы».
Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой.
Метод "пузырька".
По другому этот метод называется методом перестановок или методом обмена. При его реализации более "легкие" элементы как бы всплывают вверх. Соответственно, более тяжелые "идут ко дну".
Задан целочисленный массив из 10 элементов и нам его необходимо отсортировать по возрастанию.
Вот код программы на Паскале:
{ сортировка массива "пузырьком" по возрастанию }
Const
n = 10; { количество элементов в массиве }
Var
a: array [1..n] of integer;
i,j,buf:integer;
Begin
{Заполняем массив случайными целыми числами из диапазона от 0 до 9 и выводим массив на экран}
for i:=1 to n do
Begin
a[i]:=random(10);
write(a[i],' ');
end;
for i:=1 to n-1 do
for j:=i+1 to n do {В этой строке начинающие программисты чаcто допускают ошибку}
if a[i]>a[j] then
Begin
buf:=a[i];
a[i]:=a[j];
a[j]:=buf;
end;
writeln;
writeln('Массив после сортировки пузырьковым методом: ');
for i:=1 to n do
write(a[i],' ');
End.
Пояснения. Как видно из текста программы на Паскале, при сортировке массива методом пузырька, сравниваются два соседних элемента массива. В том случае, если элемент массива с номером iоказывается больше элемента массива с номером i+1, происходит обмен значениями при помощи вспомогательной переменной buf (переменной я дал название со смысловой нагрузкой, от слова "буфер").
Быстрая сортировка
Устанавливаем I=1 и J=N. Сравниваем элементы A[I] и A[J]. Если A[I]<=A[J], то уменьшаем J на 1 и проводим следующее сравнение элементов A[I] с A[J]. Последовательное уменьшение индекса J и сравнение указанных элементов A[I] с A[J] продолжаем до тех пор, пока выполняется условие A[I] <= A[J]. Как только A[I] станет больше A[J], меняем местами элементы A[I] с A[J], увеличиваем индекс I на 1 и продолжаем сравнение элементов A[I] с A[J]. Последовательное увеличение индекса I и сравнение (элементов A[I] с A[J]) продолжаем до тех пор, пока выполняется условие A[I] <= A[J]. Как только A[I] станет больше A[J], опять меняем местами элементы A[I] с A[J], снова начинаем уменьшать J.
Чередуя уменьшение J и увеличение I, сравнение и необходимые обмены, приходим к некоторому элементу, называемому пороговым или главным, характеризующим условие I=J. В результате элементы массива оказываются разделенными на две части так, что все элементы слева - меньше главного элемента, а все элементы справа - больше главного элемента. К этим массивам применяем рассмотренный алгоритм, получаем четыре части и т.д. Процесс закончим, когда массив A станет полностью отсортированным.
При программировании алгоритма "Быстрой сортировки" удобно использовать рекурентные вызовы процедуры сортировки (рекурсию).
{Быстрая сортировка}var a:array[1..10] of integer; { массив элементов } n:integer; procedure QuickSort(L, R: Integer); { Быстрая сортировка массива A[] }var i,j,x,y: integer;begin i:= l; j:= r; x:= a[(l+r) div 2]; repeat while (A[i] < x) do inc(i); while (x < A[j]) do dec(j); if (i <= j) then begin y:=A[i]; a[i]:=a[j]; a[j]:=y; inc(i); dec(j); end; until (i > j); if (l < j) then QuickSort(l,j); if (i < r) then QuickSort(i,r);end; begin writeln('введите 10 элементов массива:'); for n:=1 to 10 do readln(a[n]); QuickSort(1, 10); { на входе: левая и правая граница сортировки } writeln('после сортировки:'); for n:=1 to 10 do writeln(a[n]);end.Рассмотрим работу алгоритма на примере. Пусть у нас есть массив с элементами: 4,9,7,6,2,3,8
Выберем число относительно которого мы будем сравнивать – 6. Обычно выбирается число стоящее в середине. И определим два указателя b (begin) и e (end). Теперь мы двигаем наши указатели до тех пор пока не встретим число большее(если указатель b) или меньшее(указатель e) 6.
Так как числа на нужных местах, то мы продвигаем наши указатели вперед. Теперь мы наткнулись на числа 9 и 3. Мы должны поменять их местами так как 9>6, а 3<6.
Снова сдвигаем указатели на одну итерацию. Видим числа стоящие не на своем месте 7>6 и 2<6. Меняем их местами.
Вновь передвигаем указатели, они оказываются на 6.
Методы оценки ресурсной эффективности алгоритмов
Основными алгоритмическими конструкциями в процедурном программировании являются следование, ветвление и цикл. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть различия в оценке основных алгоритмических конструкций.
Трудоемкость конструкции "Следование" есть сумма трудоемкостей блоков, следующих друг за другом: f=f1+f2+...+fn.
Трудоемкость конструкции "Ветвление" определяется через вероятность перехода к каждой из инструкций, определяемой условием. При этом проверка условия также имеет определенную трудоемкость. Для вычисления трудоемкости худшего случая может быть выбран тот блок ветвления, который имеет большую трудоемкость, для лучшего случая – блок с меньшей трудоемкостью.fif=f1+fthenxpthen+felsex(1-pthen)
Трудоемкость конструкции "Цикл" зависит от вида цикла. Для цикла с параметрами будет справедливой формула: ffor=1+3n+nf, гдеn – количество повторений тела цикла, f – трудоемкость тела цикла.
Реализация цикла с предусловием и с постусловием не меняет методики оценки его трудоемкости. На каждом проходе выполняется оценка трудоемкости условия, изменения параметров (при наличии) и тела цикла. Общие рекомендации для оценки циклов с условиями затруднительны. Так как в значительной степени зависят от исходных данных.
В случае использования вложенных циклов их трудоемкости перемножаются.
Таким образом, для оценки трудоемкости алгоритма может быть сформулирован общий метод получения функции трудоемкости.
1. Декомпозиция алгоритма предполагает выделение в алгоритме базовых конструкций и оценку их трудоемкости. При этом рассматривается следование основных алгоритмических конструкций.
2. Построчный анализ трудоемкости по базовым операциям языка подразумевает либо совокупный анализ (учет всех операций), либо пооперационный анализ (учет трудоемкости каждой операции).
3. Обратная композиция функции трудоемкости на основе методики анализа базовых алгоритмических конструкций для лучшего, среднего и худшего случаев.
Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии. Поэтому трудоемкость рекурсивных реализаций алгоритмов связана с количеством операций, выполняемых при одном рекурсивном вызове, а также с количеством таких вызовов. Учитываются также затраты на возвращения значений и передачу управления в точку вызова. Для анализа трудоемкости механизма рекурсивного вызова-возврата будем учитывать следующие параметры: p – количество передаваемых фактических параметров, r – количество сохраняемых в стеке регистров, k – количество возвращаемых по адресной ссылке значений, l – количество локальных ячеек функции. Тогда функция трудоемкости на один вызов-возврат примет вид:
f=2(p+k+r+l+1),где дополнительная единица учитывает операции с адресом возврата.
Оценка требуемой памяти стека может быть получена следующим образом: так как рекурсивные вызовы обрабатываются последовательно, то в конкретный момент времени в стеке хранится не фрагмент дерева рекурсии, а цепочка рекурсивных вызовов – унарный фрагмент дерева. Поэтому объем стека определяется максимально возможным числом одновременно полученных рекурсивных вызовов.
Анализ совокупной трудоемкости рекурсивного алгоритма можно выполнять разными способами в зависимости от формирования итоговой суммы базовых операций: по цепочкам рекурсивных вызовов и возвратов, по вершинам рекурсивного дерева.
Пример 1. Оценка временной сложности функции пузырьковой сортировки.
//Описание функции сортировки методом "пузырька"void BubbleSort (int k,int x[max]) { int i,j,buf; for (i=k-1;i>0;i--) for (j=0;j<i;j++) if (x[j]>x[j+1]) { buf=x[j]; x[j]=x[j+1]; x[j+1]=buf; } }Оценим временную сложность функции пузырьковой сортировки в худшем случае, т.е. когда исходные данные отсортированы в обратном порядке. В этом случае внутренний цикл для каждого i выполнится i-1 раз и произойдет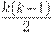 
обменов. Соответственно сложность алгоритма в худшем случае составит O(k2) обменов.
Оценим временную сложность алгоритма пузырьковой сортировки в среднем случае, т.е. когда исходные данные имеют произвольный порядок. В этом случае условие во внутреннем цикле может выполниться 1,2,...,i-1 раз. Складывая, получим 
и, соответственно, условие во внутреннем цикле для каждого i выполнится в среднем 
раз и произойдет 
обменов. Соответственно сложность алгоритма в среднем случае составит O(k2).
Пример 2. Оценка временной сложности функции вычисления биномиального коэффициента 
.
Оценим временную сложность функции в худшем случае, т.е. когда m=n. Будет выполнено (n+1) обращений к функции, которая выполнит в n случаях три операции, а в одном возвратит значение. Функция при каждом обращении передает два параметра, не использует локальных переменных, а при возвращении (n+1) раз передает управление в точку вызова. Соответственно сложность алгоритма в худшем случае составит O(n) или O(m).
Оценим временную сложность функции в среднем случае, т.е. когда m<n. При этом выполняются рассуждения, аналогичные худшему случаю, только количество рекурсивных вызовов составит (m+1). Соответственно сложность алгоритма в среднем случае составитO(m).
Лучший случай достигается при m=0, когда выполняется единственный вызов функции, передача двух параметров и возвращение в точку вызова, то есть оценка лучшего случая O(1).