Если 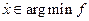 при наложенных ограничениях — решение задачи, то найдётся ненулевой вектор множителей Лагранжа
при наложенных ограничениях — решение задачи, то найдётся ненулевой вектор множителей Лагранжа 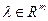 такой, что для функции Лагранжа
такой, что для функции Лагранжа
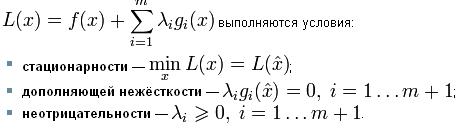
Достаточные условия минимума функции
Перечисленные необходимые условия минимума функции в общем случае не являются достаточными.
Простая формулировка
Если для допустимой точки 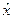 выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также λ1 > 0, то
выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также λ1 > 0, то 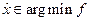
Теорема Куна–Такера
Рассмотрим задачу математического программирования
f (x)®max,
gi (x)³0, i= 1 ,…,m, (P)
x Î X ÌR n.
где f,g 1,…, gm – вогнутые непрерывные функции, а X ÌR n – выпуклое компактное множество.
Обозначим  .
.
Теорема. Пусть x * – решение задачи (P) и пусть существует точка x 0 длякоторой
gi (x 0)>0 для всех i= 1,…, m. (S)
Тогда существуют неотрицательные числа l 1,…, lm для которых
L (x,l *)£ L (x *, l *)£ L (x *, l) (L)
для всех xÎX и l= (l 1,…, lm)ÎR m и
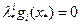 для всех i= 1,…, m. (N)
для всех i= 1,…, m. (N)
6. Оптимизационные методы получения детерминированных оценок (динамическое программирование);
Ответ:
Метод динамического программирования вначале был сформулирован для класса систем, будущее поведение которых полностью или статически определяется их состоянием в настоящем.
На основе метода ДП с успехом решается многие задачи нелинейного программирования. метод ДП позволяет производить декомпозицию многих сложных оптимизационных задач.
Решение задач на оптимум осуществляется при наличии каких-либо ограничений. Ограничения значительно усложняют процесс решения, поэтому напрашивается естественный метод: решать задачу на оптимум при широком наборе ограничений, включающим и заданное ограничение, а затем из полученных решений выбрать то, которое соответствует заданному типу ограничений. Указанный метод назвали инвариантным погружением (решаемой задачи в поле задач). Инвариантное погружение лежит в основе (на ряду с принципом оптимальности) метода ДП.
Рассмотрим простейшую задачу об оптимальном управление с закрепленным левым концом траектории и заданными временем окончания процесса управления [задача Больца]
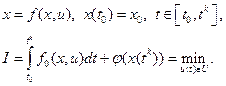 (1)
(1)
Задачу (1) можно «инвариантно погрузить» в семейство задач
 (2)
(2)
Переменными параметрами в (2) является 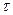 и
и  при
при  мы получаем задачу (1)
мы получаем задачу (1)
Принцип оптимальности. Оптимальная стратегия не зависит от предыстории системы, а определяется только начальными условием и конечной целью.
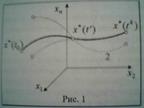
На рис.1 сплошной линей показана оптимальная траекторная задачи (1). Рассмотрим на этой траектории точку 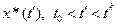 . Принцип оптимальности утверждает, что отрезок оптимальной траектории от точки
. Принцип оптимальности утверждает, что отрезок оптимальной траектории от точки  до точки
до точки 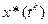 также является оптимальной траекторией, т.е. является решением задачи (2) при
также является оптимальной траекторией, т.е. является решением задачи (2) при  .
.
В ДП точка 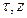 задачи (2) последовательно сдвигается с конца
задачи (2) последовательно сдвигается с конца  в начало
в начало  и на каждом шаге решается задача на оптимум при произвольном (в рамках ограничений на фазовых координаты) векторе
и на каждом шаге решается задача на оптимум при произвольном (в рамках ограничений на фазовых координаты) векторе 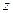 . Кроме того, при оптимизации на следующем шаге используется оптимальное управление предыдущего шага. Этим самым сложность решения задачи значительно снижается.
. Кроме того, при оптимизации на следующем шаге используется оптимальное управление предыдущего шага. Этим самым сложность решения задачи значительно снижается.
Вначале приведем задачу (1) к дискретной фирме. Разделим интервал 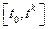 на
на 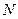 под интервалов одинаковой длительности
под интервалов одинаковой длительности  и введем обозначения:
и введем обозначения: 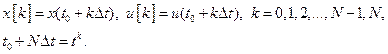 (3)
(3)
Аппроксимируя производную конечной разностью, а интеграл интегральной суммой, получаем задачи (1), (2) в дискретной форме:
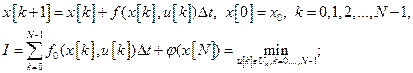 (4)
(4)
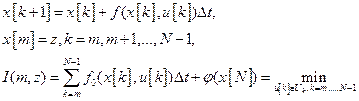 (5)
(5)
7. Оптимизационные методы получения детерминированных оценок (принцип максимума);
Ответ:
Рассматриваем процесс, описываемый системой обыкновенных дифференциальных уравнений:
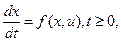 (1)
(1)
Где x - n-мерный вектор состояния (фазовых координат), u – r-мерный вектор управляющих воздействий, f – n-мерная функция. Время t явно в правую часть управления (1) не входит, и такую систему (1) называют автономной. Заметив, что произвольная система сводиться к (1) включением t в качестве (n+1)-й компоненты 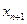 векторов x.
векторов x.
В реальной ситуации на x и u накладываются дополнительные ограничения. Далее мы остановимся на наиболее простом случае, когда u(t) для каждого t принадлежит заданной замкнутой ограниченной области U, не зависящей от x и t:
 (2)
(2)
Любое управление 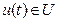 называем допустимым. Кроме того,
называем допустимым. Кроме того, 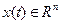 и удовлетворяет уравнению (1).
и удовлетворяет уравнению (1).
Примерами ограничений (2) могут служить
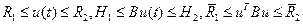
Предполагаем также, что f(x,u) непрерывна и имеет непрерывные частные производные по 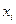
Необходимо найти такое u(t) из U при  , чтобы система, двигаясь по траектории в соответствии с (1), обеспечивала минимум некоторого показателя качества I. Для многих задач оптимального управления I представляет собой функцию от части фазовых координат в начале и в конце траектории
, чтобы система, двигаясь по траектории в соответствии с (1), обеспечивала минимум некоторого показателя качества I. Для многих задач оптимального управления I представляет собой функцию от части фазовых координат в начале и в конце траектории
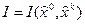 (3)
(3)
Здесь 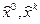 - некоторые составляющие вектора x в начале (t=0) и в конце траектории
- некоторые составляющие вектора x в начале (t=0) и в конце траектории 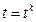 . Рассмотрим примеры.
. Рассмотрим примеры.
Часть фазовых координат, не вошедших в функцию качества (3), может быть закреплена при исходной постановке задачи
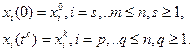 (10)
(10)
Тогда вектора 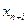 в (3) будут состоять из компонент
в (3) будут состоять из компонент
 (11)
(11)
Итак, нам надо найти 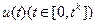 , удовлетворяющее (2) и обеспечивающие минимум функции качества (3), при условии, что система описывается уравнениями (1) с заданными значениями части фазовых координат на концах траектории (10).
, удовлетворяющее (2) и обеспечивающие минимум функции качества (3), при условии, что система описывается уравнениями (1) с заданными значениями части фазовых координат на концах траектории (10).
8. Оптимизационные методы получения детерминированных оценок (оптимизация в функциональных пространствах);
Ответ:
Функциональное пространство.
Обозначим через 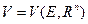 - векторное пространство всех функций
- векторное пространство всех функций 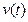 преобразования множества
преобразования множества 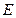 , которому принадлежит аргумент
, которому принадлежит аргумент 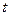 , в
, в 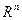 (n-мерное евклидовое пространство) с определенным образом, заданным расстоянием d на V. Примерами
(n-мерное евклидовое пространство) с определенным образом, заданным расстоянием d на V. Примерами 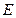 является отрезок
является отрезок 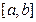 , прямоугольник
, прямоугольник 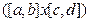 и т.п. Функция
и т.п. Функция 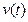 могут быть ограничены, тогда вместо
могут быть ограничены, тогда вместо  мы будем рассматривать подпространство (пространства
мы будем рассматривать подпространство (пространства 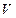 ) ограниченных функций. В каждом конкретном случае эти факты можно специально оговаривать. Элемент пространства
) ограниченных функций. В каждом конкретном случае эти факты можно специально оговаривать. Элемент пространства 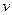 обозначим через
обозначим через  .
.
Норму элемента 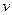 из пространства
из пространства 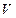 будем обозначать через
будем обозначать через 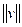 . Действительное число
. Действительное число 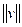 имеет свойства:
имеет свойства:
А)  для всех
для всех 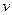 из
из 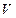 и
и 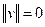 в том и только в том случае, если
в том и только в том случае, если 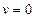 ;
;
Б)  для всех
для всех 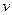 и
и  (1)
(1)
В) 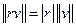 , где
, где 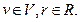
Расстояние на 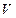 между его элементам
между его элементам 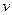 и
и  вводим следующим образом:
вводим следующим образом:
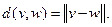
Пусть ограничения, накладываемые на элементы пространства  , выделяют из него некоторое подпространство
, выделяют из него некоторое подпространство 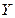 . Элемент
. Элемент 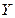 будем обозначать через
будем обозначать через  . В основном это будет подпространство ограниченных функций.
. В основном это будет подпространство ограниченных функций.
Функционал.
Функционал – это оператор, переводящий пространство 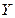 в пространство
в пространство 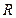 . Он каждому элементу из
. Он каждому элементу из 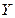 ставит в соответствие элемент из
ставит в соответствие элемент из 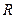 , т.е., как говорят, задан на пространстве ограниченных функций. Обозначаем функционал через
, т.е., как говорят, задан на пространстве ограниченных функций. Обозначаем функционал через 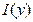 .
.
1. 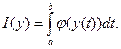
2. 
3. 
Здесь 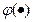 - непрерывные функции.
- непрерывные функции.
6. 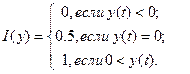
7. 
8. 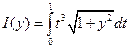
9. 
9. многокритериальная оптимизация (принцип Парето);
Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения.
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являются конкурирующими и отсутствует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек не улучшаемых решений. Не ухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. многокритериальная оптимизация должна включать в себя определенную генерацию и выбор точек с неулучшаемыми решениями.