Геометрические характеристики плоских сечений
При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечениям одинаково. Здесь геометрической характеристикой сечения является площадь.
При кручении и изгибе прочность и жесткость элементов конструкции зависит не только от площади поперечного сечения, но и от формы этого сечения.
Новые понятия:
Осевым моментом инерции сечения относительно некоторой оси, лежащей в этой же плоскости, называется взятой по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой оси:
Осевой момент инерции сечения относительно оси ОХ
Jx= ∫ y2dA,
Осевой момент инерции сечения относительно оси ОY
J y = ∫ x2dA
Осевые моменты инерции характеризуют сопротивление сечения повороту относительно соответствующей оси.
Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой точки:
J p = ∫ p2dA,
где p- расстояние до полюса.
Полярный момент инерции характеризует сопротивление сечения повороту вокруг точки (полюса).
Внутренние силовые факторы при кручении
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Кручение круглого бруса происходит при нагружении его парами сил с моментами в плоскости, перпендикулярных продольной оси.
Рассмотрим кручение цилиндра, один конец которого жестко заделан, а второй нагружен парой сил в плоскости перпендикулярной продольной оси.

Вводятся допущения:
- ось цилиндра (ось кручения) остается прямолинейной,
- расстояние вдоль оси бруса между поперечными сечениями не изменится,
|
|
- поперечные сечения бруса поворачиваются на некоторый угол φ, оставаясь при этом плоскими.
При этом образующие бруса искривляются и разворачиваются на угол γ,
называемый углом сдвига (угол поворота образующей).
Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения).
Длина бруса и размеры сечения не меняются.
Связь между угловыми деформациями определяется соотношением
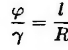
где ℓ - длина бруса,
R – радиус сечения.
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только крутящий момент.
Момент внутренних сил относительно продольной оси бруса называют крутящим моментом – Мк.
Крутящий момент в сечении равен сумме моментов внешних сил, действующих на ограниченную часть.

|

|
Крутящие моменты могут меняться вдоль оси бруса.
Для наглядного представления о распределении и значении крутящих моментов строят эпюры крутящих моментов вдоль оси бруса.
Для построения эпюр необходимо условиться о правиле знаков.
Любою из оставленных частей вала рассматриваются со стороны сечения:
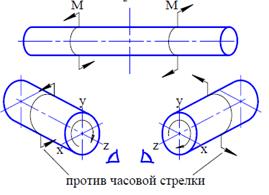
| 
|
| Мк - отрицательный | Мк - положительный |
Крутящий момент считается положительным, если моменты внешних пар сил направлены по часовой стрелке на любой из оставленных частей вала при рассмотрении его со сторо-ны сечения и наоборот.
Напряжения при кручении
Мкр действует в плоскости сечения вала, поэтому возникают касательные напряжения τ. Касательное напряжение подчиняется закону Гука и оно пропорционально углу сдвига. Напряжение в любой точке поперечного сечения определяется по формуле:
|
|
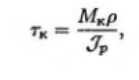
где J p – полярный момент инерции, мм4, характеризует сопротивление сечения скручиванию.
p - расстояние от точки до центра круга, мм

где W p – момент сопротивления при кручении или полярный момент сопротивления.
Единицы измерения м3, мм3
Для круглого сечения J p = πd4/32, W p = πd3/16
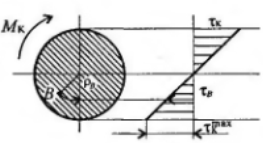
| Касательное напряжение по сечению распределено неравномерно. Максимальное напряжение на поверхности и уменьшается к центру вала. | |
4 Расчет валов на прочность и жесткость при кручении .
Разрушение вала при кручении происходит с поверхности.
При расчете на прочность используют условие прочности

где [τк] – допускаемое напряжение кручения
Существует 3 вида расчетов на прочность:
1 Проверочный расчет – проверяется выполнение условия прочности
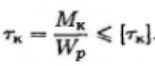
2 Проектировочный расчет – определяется диаметр вала в опасном сечении
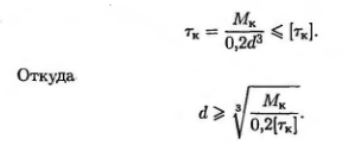
3 Проверочно – уточненный расчет (определение максимального Мк)
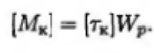
Расчет на жесткость
Деформация при кручении оценивается углом закручивания.
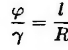
Выразим угол сдвига
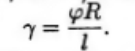
Закон Гука имеет вид
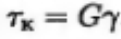
Подставим угол сдвига в закон Гука, заменив R = d/2

Используем

Угол сдвига из этих выражений будет равным
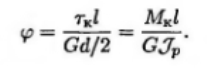
Произведение  называется жесткостью сечения
называется жесткостью сечения
Обычно рассчитывается угол закручивания, приходящийся на один метр длины вала
φ / ℓ = φо – относительный угол закручивания
Условие жесткости при кручении может быть записано
φо = Мк /GJ
φо = 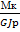 ≤ [φо]
≤ [φо]
|
|
[φо] – измеряются рад/м или град/м
При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению.