Общая задача нелинейного программирования.

В самом широком смысле общая задача нелинейного программирования заключается в отыскании экстремума целевой функции при заданных ограничениях в виде равенств и/или неравенств. Ограничения могут быть линейными и/или нелинейными. Однако общепринята несколько более узкая постановка общей задачи нелинейного программирования, в которой исключаются из рассмотрения следующие специальные случаи:

1. Переменные принимают лишь целочисленные значения (нелинейное целочисленное программирование).

2. Ограничения включают в качестве параметра время, при этом используются дифференциальные уравнения (оптимальное управление, динамическая оптимизация).

Пусть непрерывная функция f( x ) представляет собой целевую функцию; h₁(X),... h_m(X) задают ограничения в виде равенств, а g_m+1(X),... g_p(X) — ограничения в виде неравенств, где X = { x₁,… х_п } ^T - вектор-столбец компонентов x₁,… х_п в n -мерном евклидовом пространстве Eⁿ.

Как и в линейном программировании, переменные х₁,... х_п могут быть конструктивными параметрами, установками регулятора, показаниями измерительных приборов и т.д., тогда как целевая функция может представлять собой стоимость, вес, годовой доход и т.п., а ограничения - технические требования, условия работы, пропускную способность или факторы безопасности, присущие данному процессу.

Формально задача нелинейного программирования может быть сформулирована следующим образом:

минимизировать (9)

при m линейных и/или нелинейных ограничениях в виде равенств

(10)

и (р - т) линейных и (или) нелинейных ограничениях в виде неравенств

(11)

Хотя в некоторых частных случаях ограничения в виде равенств могут быть явно разрешены относительно выбранных переменных, которые затем исключаются из задачи как независимые переменные, и в задаче остаются только ограничения в виде неравенств, чаще всего ограничения в виде равенств не могут быть явно разрешены и потому сохраняются.

Иногда встречается другое представление выражений (9) - (11):

минимизировать (12)

где R - область пространства переменной X, для которой выполнены условия (10) и (11), например:

(13)

В выражениях (12) и (13) знак | читается как «при», а символ Î означает «принадлежит». Знак неравенства в выражении g_j (X) ³ 0 может быть изменен на обратный путем умножения на (-1), что не изменит математической постановки задачи.

В качестве простого примера задачи нелинейного программирования, которую можно проиллюстрировать графически, приведем следующую:

минимизировать f(X) = х₁² + x₂² + 2х₂

при ограничениях

h₁(X) = х₁² + x₂² – 1 = 0;

g₂(X) = x₁ + 2x₂ – 0.5 ³ 0;

g₃(X) = x₁ ³ 0;

g₄(X) = x₂ ³ 0.

На рис. 5 целевая функция изображена пунктирными линиями, ограничение в виде равенства - жирной сплошной кривой, а граница допустимой области, определяемой неравенствами, - линиями со штриховкой, нанесённой с внутренней стороны области.

Рис.5. Топография целевой функции и ограничений

В каждой точке n -мерного пространства переменных [ х₁, х₂,... х_п ] функция f(X) имеет определённое значение, и, следовательно, это n -мерное пространство представляет собой скалярное поле для критерия оптимальности. Как показано на рис.5, в этом пространстве можно вычертить семейство линий равных значений (эквипотенциальных гиперповерхностей) для выбранных значений функции f(X).

Пространство переменных [ х₁, х₂,... х_п ] является также скалярным полем для функций ограничений, для которых также можно изобразить графически эквипотенциальные гиперповерхности. При помощи классических методов анализа в общем случае невозможно заранее выявить расположение точки X*, которая соответствует минимальному (или максимальному) значению функции f(X), поскольку она может находиться на пересечении ограничивающих поверхностей или между ними.

Задачи линейного и квадратичного программирования могут рассматриваться как два частных случая общей задачи нелинейного программирования. Если и функция (9), и уравнения (10), и неравенства (11) линейны, то мы имеем дело с задачей линейного программирования. Если же целевая функция квадратичная, а ограничения линейные, то имеет место задача квадратичного программирования:

минимизировать 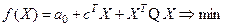(14)

при ограничениях

(15)

(16)

где Q - положительно определенная или неотрицательно определенная квадратная симметрическая матрица; а и b - матрицы коэффициентов, определение которых дано ранее в связи с уравнением (7). Иногда в задачу квадратичного программирования включают линейные ограничения в виде равенств

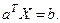(17)

Во всех трех классах задач - нелинейных, линейных и квадратичных - нужно найти вектор X * = { х₁, х₂,... х_п } ^T, минимизирующий или, наоборот, максимизирующий функцию f(X) при следующих условиях: и

Основные понятия теории оптимизации.

Оптимальные решения.

Вектор X * = { х₁, х₂,... х_п } ^T, удовлетворяющий соотношениям (10) - (11), называется оптимальной точкой, а соответствующее значение f(X*) - оптимальным значением целевой функции. Пара X * и f(X*) составляет оптимальное решение. Как показано на примере мультимодальной (многоэкстремальной) функции на рис. 6, могут существовать различные типы оптимальных решений, если целевая функция не является унимодальной (т. е. имеющей один экстремум). Глобальное оптимальное решение представляет собой наименьшее значение f(X), тогда как локальное (или относительное) оптимальное решение представляет собой наименьшее значение f(X) в окрестности некоторого вектора X. Как для глобального, так и для локального минимума

f(X*) ≤ f(X),

но для глобального оптимального решения это соотношение выполняется для всех X в эвклидовом пространстве Е^п, тогда как для локального оптимального решения это имеет место только для малой области ξ, где норма || X - X * || < ξ. Если принимается во внимание и точность решения, то условие оптимальности можно представить в виде

f(X*) ≤ f(X) – γ,

где γ — некоторая малая величина.

Все алгоритмы, описываемые в пособии [3], дают лишь локально оптимальные решения, так как на каждом этапе решения при движении к точке экстремума X * они зависят в основном от локальных свойств (местной топографии) целевой функции и ограничений. Работа всех поисковых алгоритмов примерно одинакова: на основании исследования топографии целевой функции в текущей точке определяется характер её изменения и в пространстве проектных переменных делается рабочий шаг в направлении её уменьшения (или увеличения). Далее, процесс повторяется. Исключение составляют чистые методы Монте-Карло, которые исследуемые точки выбирают случайным образом. Однако эти методы вообще не гарантируют ничего: экстремум они находят случайно, если вообще находят.

На практике предположение о том, что локальный экстремум является глобальным, может быть проверено путем использования нескольких начальных векторов, но даже если найдено только одно локальное решение, в общем случае нельзя показать, что это решение обязательно является глобальным оптимумом.

Рис. 6. Классификация оптимальных решений.

К счастью, для задач, соответствующих действительным физическим процессам, целевая функция обычно является хорошей и обладает единственным экстремумом. Поэтому для большинства практических целей использование численных процедур, дающих локальное решение задачи оптимизации, не является большим недостатком.