Метод множителей Лагранжа.

Этот метод широко используется при оптимизации авиационных агрегатов при их проектировании с учётом многообразных и разнородных ограничений, например: проектирование конструкции с учётом ограничений по прочности, жёсткости, частотам собственных колебаний, устойчивости и т.п. Поэтому краткое знакомство на уровне идей с методом множителей Лагранжа представляется полезным.

Методы, основанные на использовании множителей Лагранжа, относятся к категории параметрических методов штрафных функций, поскольку для них характерно то, что функции-ограничения вводятся в структуру модифицированной целевой функции совместно с некоторым переменным параметром. Чтобы обобщить метод множителей Лагранжа, ограничения в виде неравенств следует преобразовать в ограничения, имеющие вид равенств, путём введения надлежащих ослабляющих переменных (на каждое ограничение-неравенство по одной ослабляющей переменной). Задача нелинейного программирования в общей постановке принимает при этом следующий вид:

минимизировать f(X), X Î Еⁿ; (29)

при ограничениях

h_j (X) = 0; j = 1,2... m; (30)

g_j (X) – v_j² = 0; j = (т + 1)... р. (31)

Если вычесть v_j² из g_j (X) (j = т + 1,... р), то можно гаранти­ровать, что ограничивающее условие, имеющее в исходной постановке задачи вид неравенства, действительно выполняется. Тогда можно определить обычным образом функцию Лагранжа

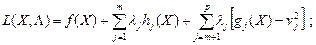(32)

где 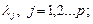- неотрицательные и не зависящие от X весовые коэффициенты, которые можно отождествить с множителями Лагранжа. Для того чтобы X * было решением общей задачи нелинейного программирования (29)-(31), необходимо и достаточно, чтобы: 1) функция f(X*) была выпуклой; 2) в окрестности X* ограничения задачи были выпуклы и 3) в точке X* удовлетворялась следующая система уравнений, определяющая стационарное решение уравнения (32):

; при i = 1, 2... п;

; при j = l, 2 … р;

; при j = (m +1)… p;

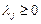; j = 1,2… p.

Короче говоря, условный минимум f(X) имеет место в стационарной точке для L(X, Λ, V) и, в частности, в седловой точке (X, Λ, V) - пространства, так что задача с ограничениями превращается в задачу определения седловой точки в отсутствие ограничений.

Заключение.

На этом мы завершаем краткое рассмотрение общей теории оптимизации. Конечно, мы не исчерпали весь круг проблем, необходимых для решения при оптимизации, однако теперь читатель сможет уверенно и компетентно формулировать задачи оптимизации организационных и технических систем, классифицировать их и выбирать для их решения наиболее эффективные поисковые алгоритмы, большой набор которых приведен в книге [4].

За рамками пособия осталась большая область теории, связанной с многопараметрической оптимизацией, с инженерными методами оптимизации, а также с оптимизацией в условиях неопределённости. Поэтому данная тонкая книжка должна рассматриваться как введение в большой и плодотворный мир оптимального проектирования организационно-технических систем.

Литература

1. Уайлд Д. Оптимальное проектирование. -М: Мир, 1981. -272с.
2. Батищев Д.И. Методы оптимального проектирования. М.: Радио и связь, 1984
3. Данилин А.И. Методы оптимизации. Учебное пособие. –Самара: Изд-во Самарского государственного аэрокосмического ун-та, 2011. -66c.
4. Химмельблау Д. Прикладное нелинейное программирование. М: Мир, 1975. -534с.

Оглавление

1. Введение. 3

2. Постановка задачи оптимизации. 8

2.1. Функция цели. 9

2.2. Проектные переменные. 11

2.3. Запись ограничений. 14

3. Построение модели. 15

3.1. Принятие допущений. 16

3.1.1. Некоторые часто используемые допущения. 17

3.2. Использование физических принципов. 19

3.3. Вычислительные трудности. 20

4. Задачи математического программирования. 23

4.1 Задача линейного программирования. 23

4.2. Общая задача нелинейного программирования. 28

4.3. Основные понятия теории оптимизации. 32

4.3.1. Оптимальные решения. 32

4.3.2. Вогнутость и выпуклость. 34

4.3.3. Допустимость. 38

4.3.4. Градиент. 39

4.3.5. Аппроксимация функций. 41

5. Необходимые и достаточные условия оптимальности. 42

5.1. Нелинейное программирование без ограничений. 43

6. Сведение задачи с ограничениями к безусловно экстремальной форме. 44

6.1. Метод внешнего штрафа. 48

6.2. Метод внутреннего штрафа. 50

6.3. Комбинированный метод штрафных функций. 51

6.4. Метод множителей Лагранжа. 53

7. Заключение. 55

Литература. 55