Вогнутость и выпуклость.

Понятия вогнутости и выпуклости полезны при определении того, при каких условиях локальное оптимальное решение является также глобальным оптимальным решением, что представляется важным в случае множественных оптимумов.

Функция Ф (X) называется выпуклой в области R, если для любых двух векторов X₁ и X₂ Î R выполняется неравенство

(18)

где q - скалярная величина из диапазона 0 ≤ q ≤ 1. Функция Ф (X) является строго выпуклой, если для X₁ ≠ X₂ в выражении (18) используется знак неравенства (<). Векторное неравенство X > Y означает, что х_i > y_i для каждого элемента; в случае X > Y справедливо неравенство x_i > y_i для всех i. На рис. 7 показаны строго выпуклая и строго вогнутая функции одной переменной. Выпуклая функция Ф (X) не может принимать значение, большее, чем значение, полученное линейной интерполяцией в промежутке между X₁ и X₂. Если имеет место неравенство, обратное (18), то функция называется вогнутой.

Рис. 7.

Линейные функции одновременно и выпуклые и вогнутые, так как неравенство (18) выполняется для любых точек как равенство.

Дифференцируемая выпуклая функция обладает следующими свойствами.

1. для любых X₁ и X₂. Другая запись этого условия такова: для любых X₁ и X₂.

2. Матрица вторых частных производных функции Ф (X) по вектору X, так называемая матрица Гессе, положительно определённая (или положительно полуопределённая) для всех X, если Ф (X) строго выпуклая (или просто выпуклая). Если определитель матрицы Гессе равен нулю, то матрица Гессе может считаться как положительно, так и отрицательно полуопределённой.

3. В области допустимых значений R функция Ф (X) имеет только один экстремум, то есть вогнутая функция унимодальна.

Множество точек или область в n-мерном пространстве называется выпуклым, если для любых пар точек X₁ и X₂, принадлежащих этому множеству, отрезок прямой, соединяющий их, также полностью принадлежит множеству, см. рис. 8.

Рис. 8.

Из понятия выпуклости вытекает один важный результат математического программирования. Задача нелинейного программирования, представленная в виде задачи выпуклого программирования, формулируется следующим образом:

минимизировать

при ограничениях

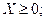
где f (X) – выпуклая функция и каждая функция - вогнутая функция. При этом локальный минимум является также и глобальным минимумом. Аналогично локальный максимум является глобальным максимумом, если целевая функция вогнутая, а ограничения образуют выпуклое множество.

Рассмотрим следующую задачу (рис. 9): минимизировать f(X) = x₁² + x₂² - 4 х₁ + 4;

при ограничениях:

g₁(X) = x₁ – x₂ + 2 ³ 0;

g₂(X) = -x₁² + x₂ – 1 ³ 0;

g₃(X) = x₁ ³ 0;

g₄(X) = x₂ ³ 0.

Рис. 9. Задача выпуклого программирования.

Внимательное изучение кривых (к тому же выводу можно прийти и аналитически) показывает, что ограничения образуют выпуклую область (допустимая часть области заштрихована), поскольку функции g₁ (X), g₃ (X) и g₄ (X) линейные и, следовательно, вогнутые (правда, они одновременно и выпуклые), а функция g₂ (X) строго вогнутая. Можно показать, что функция g₂ (x) вогнутая, заметив, что матрица Гессе функции (-g₂(x)) положительно полуопределённая.

Целевая функция f(X) строго выпуклая, и локальный оптимум, являющийся также и глобальным оптимумом, достигается в точке X * = {0.58 1.34} ^Т, где f(X) = 3.80; см. рис. 9.

В задаче линейного программирования, имеющей оптимальное решение, целевая функция всегда выпуклая, а ограничения образуют выпуклое множество, так что локальный оптимум всегда является в то же время и глобальным оптимумом.

Ограничения в задаче квадратичного программирования те же, что и в задаче линейного программирования, а целевая функция выпуклая, если (X^T Q X) является положительно полуопределённой; следовательно, матрица Q должна быть неотрицательно определенной. Однако только при особых обстоятельствах можно показать, что общая нелинейная функция f(X) является выпуклой, а ограничения образуют выпуклое множество. Так, одной из самых серьезных трудностей является то, что нелинейные равенства не могут быть частью выпуклой области, содержащей больше чем одну точку, поскольку прямая линия, соединяющая две любые несмежные точки, удовлетворяющие данному равенству, не может в то же самое время проходить и через другие точки, удовлетворяющие этому равенству, как это требуется для выпуклости. Тем не менее в особом случае, когда ограничивающее множество образовано лишь ограничениями в виде неравенств и все функции-ограничения являются вогнутыми, так что точки, для которых g_j(X) ³ 0, образуют выпуклое множество, задача нелинейного программирования может представлять собой задачу выпуклого программирования.

Допустимость.

Любой вектор X, удовлетворяющий ограничениям в виде равенств и в виде неравенств, называется допустимой точкой или допустимым вектором. Множество всех точек, удовлетворяющих ограничениям, образует допустимую область функции f(X), которую будем обозначать через R; любая точка вне R называется недопустимой. Условный оптимум представляет собой локальный оптимум, лежащий на границе допустимой области. Если ограничения имеют вид равенств, то допустимый вектор X должен лежать на пересечении всех гиперповерхностей, соответствующих h_j (X) = 0. При ограничениях в виде неравенств точка X может быть либо внутренней точкой (допустимой точкой), либо граничной точкой (тоже допустимой точкой), либо внешней точкой (недопустимой точкой). Для внутренней точки g_j (X) > 0; в случае граничной точки удовлетворяется по крайней мере одно равенство g_j (X) = 0, а для внешней точки имеет место по крайней мере одно неравенство g_j (X) < 0. Множество точек, удовлетворяющих равенствам g_j (X) = 0, j = 1,2... р, определяет граничные поверхности системы ограничений, заданных в виде неравенств. Активным, или связывающим, ограничивающим неравенством называется такое, которое для данного вектора X превращается в равенство g_j (X) = 0. Область допустимых значений переменных может быть односвязной (фиг. 10 а) и многосвязной (фиг. 10б). В последнем случае может оказаться, что конкретный алгоритм нелинейного программирования проведёт обследование не всех допустимых областей, если процедура поиска не будет включать большое число начальных векторов.

Рис. 10. Примеры односвязной (а) и многосвязной (б) допустимой области

К счастью, большинство задач нелинейного программирования, относящихся к реальным процессам, формулируются так, что допустимая область является односвязной.

Градиент.

Множество точек, для которых целевая функция имеет одинаковое значение, называется линией равных значений или линией уровня f(X). Несколько таких линий уровней изображено на рис. 11.

Если целевая функция непрерывна и дифференцируема, то существует градиент f(X), определяемый как вектор-столбец из первых частных производных f(X) по X, значения которых берутся в данной точке X. Верхний индекс k, k = 0,1..., используется для обозначения точки в евклидовом пространстве Еⁿ, в которой берется значение градиента, и, таким образом, градиент в точке X^(k) равен

Рис. 11. Градиент и направление наискорейшего спуска.

Выражение 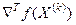означает вектор-строку. В матричной алгебре доказывается, что градиент скалярной функции направлен в сторону наискорейшего увеличения функции, то есть наискорейшего подъема, и что он ортогонален линии уровня функции f(X), проходящей через данную точку X^(k). Вектор, противоположный этому градиенту (отрицательный градиент), направлен в сторону наискорейшего спуска. Любой вектор V, ортогональный [так же, как и касательная плоскость к f(X^(k)) в точке X^(k) ], может быть записан как имеющий следующее свойство:

Следует отметить, что градиент не является направлением наискорейшего увеличения f(X), если рассмотрение ведется не в евклидовой, а в какой-то другой метрике. Например, если определять длину вектора X не по формуле || X || = (X^Т X)^1/2, а по формуле , то направление наискорейшего увеличения f(X) можно получить, находя ту компоненту , которая имеет наибольшее абсолютное значение, и полагая соответствующую компоненту X равной либо (+1), либо (-1) в зависимости от знака компоненты градиента, а остальные компоненты приравнивая нулю, как, например, в симплекс-методе при линейном программировании.

Аппроксимация функций.

Для некоторых процедур математического программирования необходимо осуществлять линейную или квадратичную аппроксимацию функций f(X), и . Например, линейная, или первого порядка, аппроксимация целевой функции f(X) может быть выполнена с помощью усеченного ряда Тейлора в окрестности :

(19)

Квадратичную аппроксимацию функции f(X) можно получить, отбрасывая в рядах Тейлора члены третьего и более высокого порядка:

(20)

где - матрица Гессе функции f(X), которая обозначается H (X) и представляет собой квадратную матрицу вторых частных производных f(X), взятых в точке :

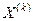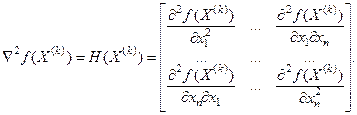(21)