Пример 6. Для условий примера 1 вычислить оценки асимметрии и эксцесса.
Построение доверительных интервалов для параметров нормального распределения
Интервальной оценкой математического ожидания μ нормального распределения при известной дисперсии  называется интервал
называется интервал
 ,
, 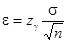 ,
,
удовлетворяющий равенству:  , где: γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание,
, где: γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание,  ─ точечная оценка математического ожидания, n ─ объём выборки; число
─ точечная оценка математического ожидания, n ─ объём выборки; число  находится из уравнения
находится из уравнения 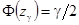 , где
, где  ─ функция Лапласа.
─ функция Лапласа.
Интервальная оценка математического ожидания находится по формуле:
 .
.
В MS Excel для вычисления величины  предназначена функция (категория Статистические):
предназначена функция (категория Статистические):
ДОВЕРИТ(Альфа;Станд_откл;Размер),
где: Альфа ─ уровень значимости  , используемый для вычисления уровня надёжности
, используемый для вычисления уровня надёжности 
 . Уровень надёжности равняется
. Уровень надёжности равняется  процентам; Станд_откл ─ стандартное отклонение
процентам; Станд_откл ─ стандартное отклонение  генеральной совокупности, предполагается известным; Размер ─ объём выборки n.
генеральной совокупности, предполагается известным; Размер ─ объём выборки n.
Пример 7. По выборке объёма n =50 найдено значение выборочного среднего  =3,5. Стандартное отклонение равно
=3,5. Стандартное отклонение равно  =2,5. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
=2,5. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
Последовательность выполнения
- Вычислить уровень значимости:
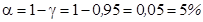 .
.
2. Ввести в ячейку А1 формулу =ДОВЕРИТ(0,05;2,5;50). В А1 появится результат: 0,693.
- Вычислить границы доверительного интервала:
 ;
;
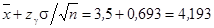 .
.
С вероятностью 0,95 математическое ожидание (генеральное среднее) принадлежит интервалу (2,807; 4,193). Математически этот вывод выражается формулой  .
.
Интервальной оценкой математического ожидания μ нормального распределения при неизвестной дисперсии  называется интервал:
называется интервал:
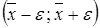 ,
,  ,
,
удовлетворяющий равенству:  ,
,
где γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание,  ─ точечная оценка математического ожидания,
─ точечная оценка математического ожидания, 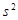 ─ исправленная выборочная дисперсия; n ─ объём выборки; число
─ исправленная выборочная дисперсия; n ─ объём выборки; число  находится из уравнения
находится из уравнения  , где
, где  ─ функция распределения Стъюдента.
─ функция распределения Стъюдента.
Интервальная оценка математического ожидания находится по формуле:
 .
.
В MS Excel для вычисления величины 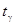 предназначена функция (категория Статистические):
предназначена функция (категория Статистические):
СТЪЮДРАСПОБР(вероятность;степени_свободы),
где: вероятность ─ уровень значимости  ; степени_свободы ─ число степеней свободы
; степени_свободы ─ число степеней свободы  .
.
Пример 8. По выборке объёма n = 20 найдено выборочное среднее  =3,5 и исправленное среднеквадратическое отклонение
=3,5 и исправленное среднеквадратическое отклонение  . Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
- Ввести в ячейку А1 формулу = СТЪЮДРАСПОБР(0,05;19). В А1 появится результат: 2,093.
2. Вычислить границы доверительного интервала:
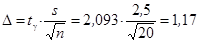 ;
;
 ;
;
 .
.
Доверительный интервал для генерального среднего имеет вид:
 .
.
Доверительный интервал для генеральной дисперсии нормально распределённого признака Х определяется на основе соотношения
 ,
,
где: γ ─ заданная доверительная вероятность, 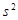 ─ исправленная выборочная дисперсия; n ─ объём выборки;
─ исправленная выборочная дисперсия; n ─ объём выборки; 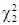 и
и  определяются из условий
определяются из условий
 ,
, 
Для вычисления  и
и 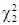 используется функция
используется функция