Простейшие следствия из аксиом

ГЛАВА 9. ГРУППЫ

 

Основные определения и примеры

Определение.Группой называется множество G элементов произвольной природы, в котором задана внутренняя операция, удовлетворяющая трtм аксиомам.

1*.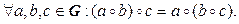

2*.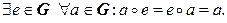

3*.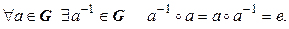

Таким образом, групповая операция ассоциативна, в группе есть нейтральный элемент, и каждый элемент в группе имеет обратный.

Если групповая операция, кроме того, коммутативна, то группа называется коммутативной или абелевой.

Если групповая операция – сложение, то группа называется аддитивной, если – умножение, то – мультипликативной.

 

Примеры

 

1. Любое линейное пространство – абелева аддитивная группа.

2. Множество всех матриц – абелева аддитивная группа.

3. 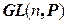– множество невырожденных матриц п- го порядка с элементами из поля Р – это мультипликативная группа.

4. 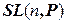- множество матриц п- го порядка с элементами из Р, определитель которых равен единице, – мультипликативная группа.

5. Множества 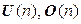унитарных и ортогональных матриц соответственно n -го порядка – мультипликативные группы.

6. Множества 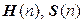эрмитовых и симметричных матриц n -го порядка – аддитивные группы.

7. 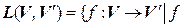– линейный 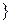– аддитивная группа.

8. 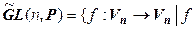– линейный невырожденный 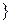– мультипликативная группа.

9. Множества 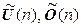унитарных и ортогональных операторов соответственно в n -мерном евклидовом пространстве – мультипликативные группы.

10. Множества 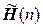и 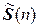эрмитовых и симметричных операторов соответственно в n- мерном евклидовом пространстве – аддитивные группы.

Подмножество H группы G называется ее подгруппой, если оно само является группой относительно операции, заданной в G. Такимобразом,

O (n) – подгруппа U (n), которая, в свою очередь, является подгруппой группы 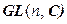; S (n) – подгруппа H (n), а она – подгруппа группы .

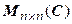Определение. Пусть 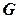и 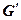– группы. Отображение 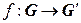называется изоморфизмом групп, если оно взаимно однозначное и сохраняет групповую операцию, т. е. если .

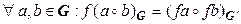Например, следующие группы изоморфны: 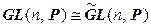, , 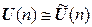, 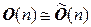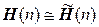. Напоминаем, что в математике изоморфные объекты не различаются, поэтому матричные группы и соответствующие группы операторов обозначаются одинаково, а волну для их различения мы ставили временно. О какой именно из групп идет речь – матричной или операторной – должно быть понятно из контекста.

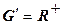Приведем еще один интересный пример изоморфизма. Пусть – аддитивная группа, а – мультипликативная. Рассмотрим следующее отображение: 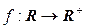: положим 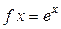. Так как 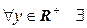единственное 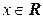такое, что , то – взаимно однозначное. Кроме того, , значит, f – изоморфизм. Таким образом, аддитивная группа 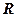изоморфна мультипликативной группе .

 

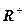Простейшие следствия из аксиом

 

1º.В каждой группе существует единственный нейтральный элемент.

2º.В группе каждый элемент имеет единственный обратный.

3º. 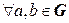каждое из уравнени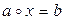й и 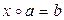в группе G имеет единственное решение.

►Первые два следствия доказываются точно так же, как и соответствующие утверждения для линейных пространств, и вы это можете легко сделать самостоятельно в качестве упражнения. Доказательство третьего проведем для уравнения

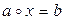. (9.1)

а) Существование решения. Положим 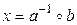. Подставляя в (9.1), получаем , и, таким образом, x – действительно решение уравнения (9.1).

б) Единственность. Предположим, что (9.1) имеет два разных решения x ₁ ≠ x ₂. Тогда:

.

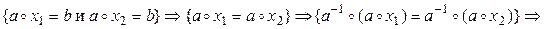
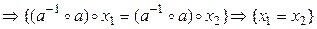Таким образом, мы пришли к противоречию.◄

 

Группа Лоренца

Рассмотрим пространство Минковского

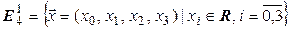
с введенным в нем скалярным произведением

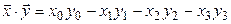
и выберем в этом пространстве следующий базис:

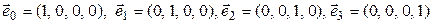. (9.2)

Матрица Грама этого базиса имеет вид

.

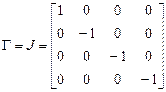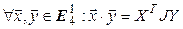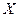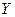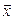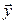Очевидно, , где и – координатные столбцы векторов и соответственно в базисе (9.2).

Определение.Преобразованием Лоренца называется линейный оператор 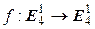, сохраняющий скалярное произведение, т. е. такой, что

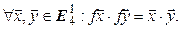
Лемма. Для того, чтобы линейный оператор 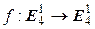был преобразованием Лоренца, необходимо и достаточно, чтобы его матрица А в базисе (9.2) удовлетворяла условию

. (9.3)

Доказательство леммы вы можете провести самостоятельно в качестве упражнения.

Следствие. Преобразование Лоренца – невырожденный линейный оператор.

► Из (9.3) следует, что 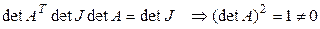. Таким образом, матрица преобразования Лоренца невырождена, а значит, и само преобразование невырождено.◄

В качестве примера преобразования Лоренца можно взять преобразование со следующей матрицей в базисе (9.1):

.

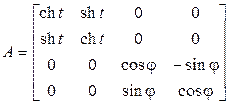Теорема. Множество всех преобразований Лоренца является группой относительно операции умножения линейных операторов.

►Обозначим L – множество всех преобразований Лоренца. Тогда :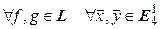

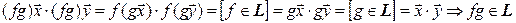
и, таким образом, 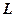замкнуто относительно операции умножения.

Ассоциативность операции произведения любых отображений была доказана в § 1 гл. 4. Если e – тождественный оператор, то очевидно, что 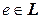. Кроме того, любой лоренцов оператор является невырожденным, поэтому 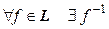. Покажем, что и 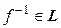. Действительно,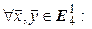

,

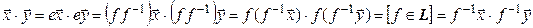откуда и вытекает, что .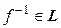

Таким образом, множество 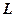удовлетворяет всем условиям из определения группы. ◄

Группа всех преобразований Лоренца и называется группой Лоренца.

 

ЛИТЕРАТУРА

 

Ильин В.А., Позняк Э.Г. Линейная алгебра / Учебник. М.: Наука, 1984.

Беклемишев Д.В. / Курс аналитической геометрии и линейной алгебры: Учебное пособие. М.: Наука,1980

Шикин Е.В. / Линейные пространства и отображения: Учебное пособие. М.: МГУ, 1987

Милованов М.В., Тышкевич Р.И., Феденко А.С. / Линейная алгебра и аналитическая геометрия: Учебное пособие. Минск. Вышэйшая школа, 1963.

Апатенок Р.Ф., Маркина А.М., Попова Н.В., Хейнман В.Б. / Элементы линейной алгебры и аналитической геометрии: Под ред. Воднева В.Т. Учебное пособие. Минск: Вышэйшая школа, 1986

Русак В., Шлома Л., Ахраменка В., Крачкоускi А. Кypс вышэйшай матэматыкi. Алгебра i геаметрыя, аналiз функцый адной зменнай: Падручнiк. Мн.: Вышэйшая школа, 1994

Мак-Коннел А.Дж. / Введение в тензорный анализ с приложениями к геометрии, механике и физике. М., Физматгиз, 1963.

Рашевский П.К. / Риманова геометрия и тензорный анализ. М., Наука, 1987.

Акивис М.А., Гольдберг В.В. / Тензорное исчисление. М., Наука, 1972.