План
- Компакты в пространстве
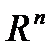. Критерий компактности множества - Теорема Больцано-Вейерштрасса
- Векторные последовательности. Понятие предела векторной последовательности
- Простейшие свойства пределов векторных последовательностей
- Фундаментальные последовательности. Подпоследовательности
1. Компакты в пространстве 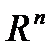. Критерий компактности множества
Пусть дана совокупность 
открытых множеств в пространстве .
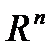Определение 1. Говорят, что совокупность множеств покрывает множество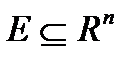 
, если 
.
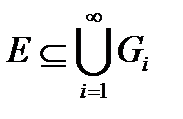Определение 2. Множество 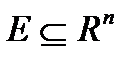называется компактным множеством, или компактом, если из каждой бесконечной совокупности открытых множеств, которая покрывает множество 
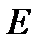, можно выделить конечную совокупность, которая тоже покрывает множество 
.
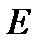Пример. Пусть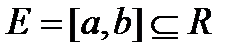 
. По лемме Бореля из каждой бесконечной системы интервалов, которая покрывает 
, можно выделить конечную подсистему, которая покрывает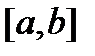 
, поэтому 
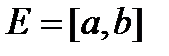- компакт.
Определение 3. Замкнутым параллелепипедом в пространстве 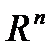называется множество точек 
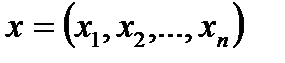, которые удовлетворяют условиям:
.
Замечание. Можно показать, что замкнутый параллелепипед является компактом.
Определение 4. Множество 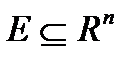называется ограниченным, если существует шар, который содержит это множество.
Теорема 1. Для того, чтобы множество 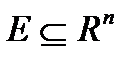было компактом, необходимо и достаточно, чтобы оно было замкнутым и ограниченным.
Теорема Больцано-Вейерштрасса
Теорема 2 (Больцано-Вейерштрасса). Любое бесконечное ограниченное множество 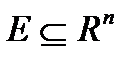имеет хотя бы одну предельную точку.
Доказательство. Предположим, что это не так: бесконечное ограниченное множество 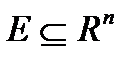не имеет ни одной предельной точки. Тогда можно сказать, что 
содержит в себе все свои предельные точки, т.е. является замкнутым. Поскольку множество 
замкнуто и ограничено, оно компактно. Для каждой точки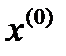 
множества можно построить шар, который не содержит других точек , поскольку каждая точка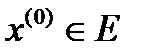 
не является предельной для этого множества. Совокупность таких шаров является бесконечной и покрывает , но из этой совокупности невозможно выделить конечную совокупность, которая покрывает . Это противоречит компактности множества . Наше предположение является ошибочным.
|
|
Векторные последовательности. Понятие предела векторной последовательности
Пусть каждому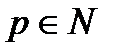 
ставится в соответствие некоторая точка (или вектор) 
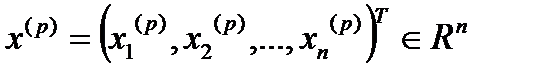. Тогда говорят, что в пространстве 
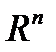определена векторная последовательность 
.
Определение 5. Точка 
называется пределом векторной последовательности и обозначается: 
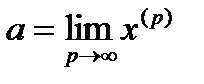, если
для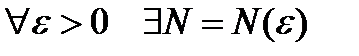 
, что для 
выполняется: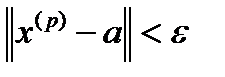 
.
Геометрический смысл: Точка является пределом векторной последовательности , если любая окрестность точки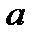 
в пространстве 
содержит бесконечно много элементов последовательности, а вне окрестности их может быть лишь конечное количество.
Пример. Пусть дана векторная последовательность , для которой 
. Доказать, что 
.
По определению 5 надо показать, что
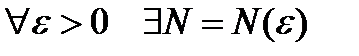, что для : 
.
.
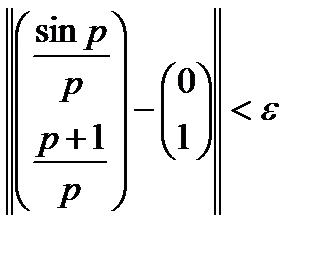Если 
, то :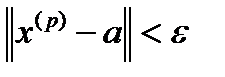
.
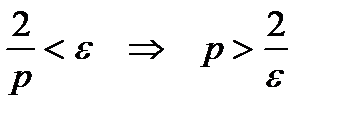Таким образом, неравенство 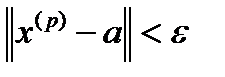выполняется для бесконечного количества элементов последовательности, номера которых 
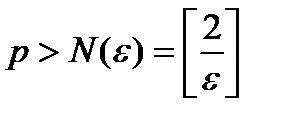, что и нужно было доказать.