Теорема 3. Если 
имеет предел, то этот предел единственный.
Доказательство. Самостоятельно.
Определение 6. Последовательность называется ограниченной, если существует такой шар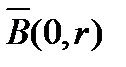 
, который содержит все элементы этой последовательности, т.е. для элементов последовательности выполняется неравенство 
.
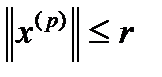Теорема 4. Пусть сходится, тогда - ограниченная последовательность.
Замечание. Не любая ограниченная последовательность является сходящейся.
Теорема 5 (о покоординатной сходимости). Для того, чтобы , 
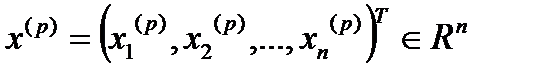,сходилась к 
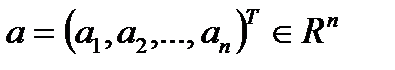необходимо и достаточно, чтобы для каждого значения 
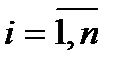соответствующая числовая последовательность координат 
.
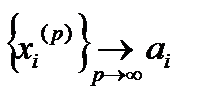Доказательство. Необходимость. Пусть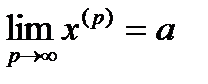 
. По определению предела векторной последовательности это означает, что
для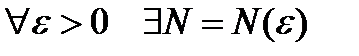 
, что для 
выполняется: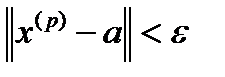 
.
Возьмем произвольно конкретное значение 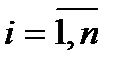. Пусть 
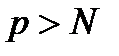. Тогда
,
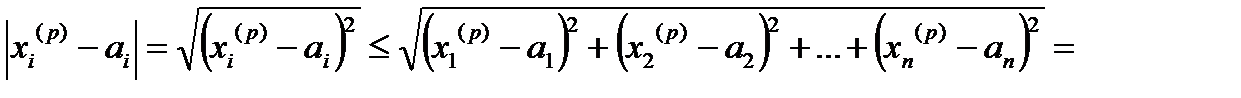
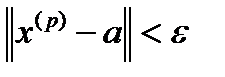а это по определению предела числовой последовательности и означает, что .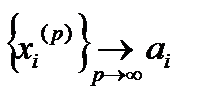
Достаточность. Пусть для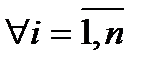 
: 
.
,
,
...
.
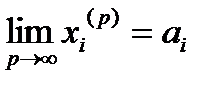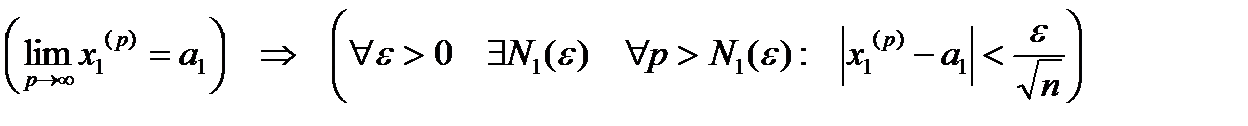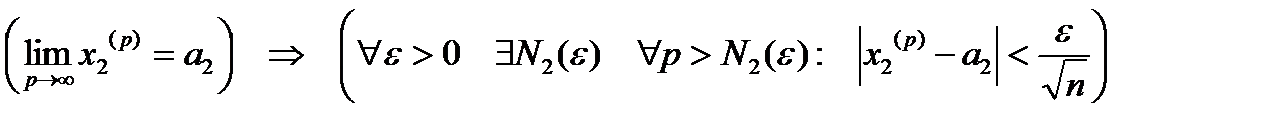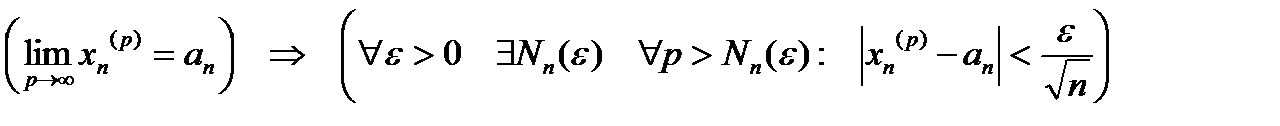Пусть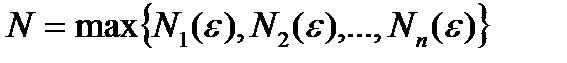 
. Тогда 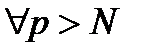для 
и для 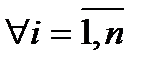все предыдущие неравенства выполняются одновременно, а тогда:
,
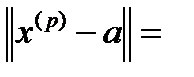
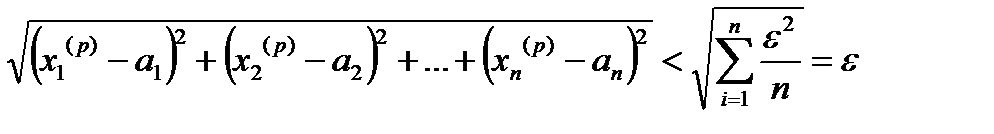Т.е.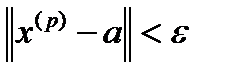 
,
что говорит о том, что .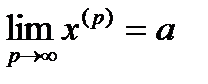
Теорема 6. Пусть , 
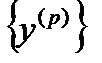- векторные последовательности в пространстве 
, 
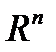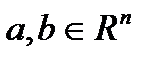и ,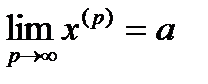 
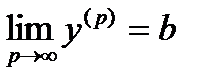. Тогда последовательности 
, 
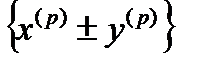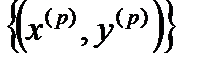(тут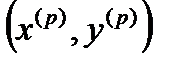 
- скалярное произведение 
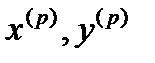) также являются сходящимися и
, 
.
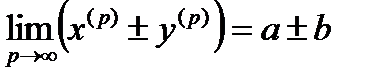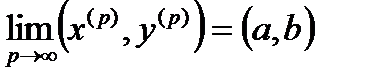Фундаментальные последовательности. Подпоследовательности
Определение7. последовательность , 
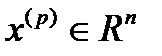, называется фундаментальной, если
для 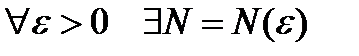, что для 
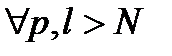выполняется: 
.
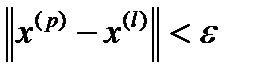Теорема 7. Для того, чтобы последовательность , , 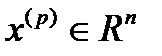сходилась необходимо и достаточно, чтобы она была фундаментальной.
Доказательство. Необходимость. Пусть 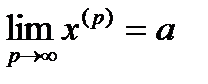. По определению это означает, что
для 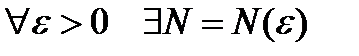, что для , 
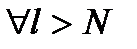выполняется: 
, 
.
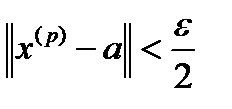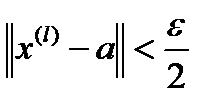Тогда
.
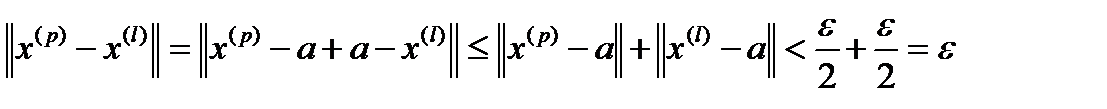Достаточность. Пусть - фундаментальная векторная последовательность. По определению это означает, что
для 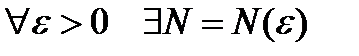, что для 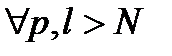выполняется: .
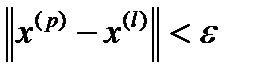Зафиксируем 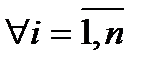. Тогда
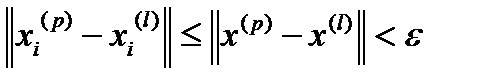для .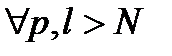
Таким образом для каждого фиксированного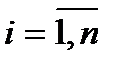 
числовая последовательность 
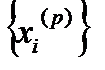является фундаментальной, а потому сходящейся. Тогда по теореме о покоординатной сходимости сходящейся будет и векторная последовательность .
Определение8. Пусть определена векторная последовательность , 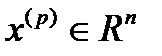. Рассмотрим последовательность натуральных чисел
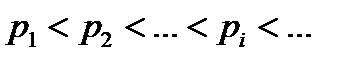
Тогдапоследовательность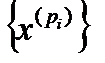 
называют подпоследовательностью .
Утверждение 1. Последовательность , 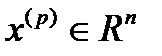сходится тогда и только тогда, когда сходится каждая ее подпоследовательность.
Утверждение 2. Если из последовательности , 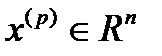можно выделить две подпоследовательности, которые стремятся к разным пределам, то данная последовательность является расходящейся.
Утверждение 3. Если из последовательности , 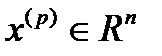можно выделить две подпоследовательности, которые стремятся к одному пределу, из этого вообще не вытекает сходимость данной последовательности .
Лемма (Больцано-Вейерштрасса). Из каждой ограниченной последовательности , , 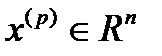можно выделить сходящуюся последовательность.
Вопросы
1. Когда совокупность множеств 
покрывает множество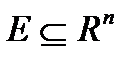 
?
2. Когда множество 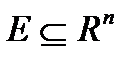называют компактным множеством? Привести примеры компактов.
3. Что такое замкнутый параллелепипед в пространстве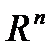 
? Привести примеры.
4. Какое множество 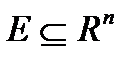называется ограниченным?
5. Критерий компактности множества.
6. Что можно сказать о наличии предельных точек у любого бесконечного ограниченного множества ?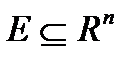
7. Определения векторной последовательности. Понятие предела векторной последовательности. Геометрический смысл предела векторной последовательности.
8. Простейшие свойства пределов векторных последовательностей.
9. Теорема о покоординатной сходимости векторной последовательности.
10. Какая векторная последовательность называется фундаментальной?
11. Критерий сходимости векторной последовательности.
12. Понятие подпоследовательности векторной последовательности. Свойства подпоследовательностей.