Теорема 3. Пусть функция 
определена и дифференцирована на 
, 
(
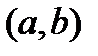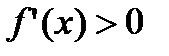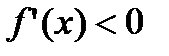) для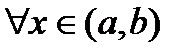 
, тогда строго монотонно возрастает (строго монотонно убывает) на .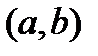
Доказательство. Докажем теорему для случа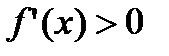я для 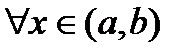. Возьмем произвольно 
, 
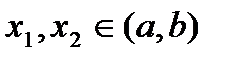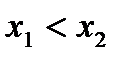. Функция на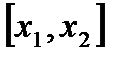 
удовлетворяет условиям теоремы Лагранжа, поэтому 
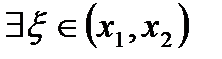, что
,
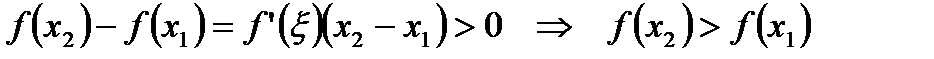т.е. строго монотонно возрастает.
Пример. Рассмотрим функцию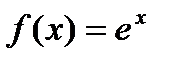 
, определенную на 
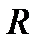. Поскольку 
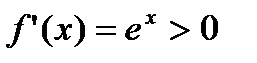, это функция строго монотонно возрастает на всем множестве действительных чисел.
Формула Тейлора
Пусть функция дифференцирована в точке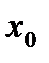 
, тогда, как известно, в достаточно малой окрестности точки 
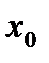функция представляется в виде:
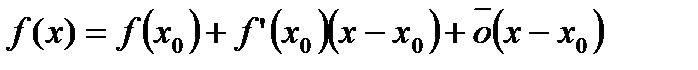, когда 
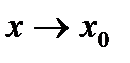. (1)
Сумма двух первых слагаемых в правой части (1) - это линейная функция, или иначе - это многочлен первой степени: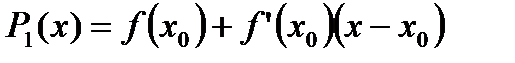 
. Тогда (1) можно записать как
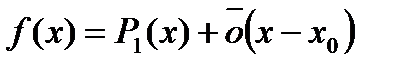, когда 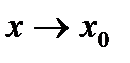. (2)
Определение 2. Говорят, что функция 
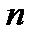раз дифференцирована в точке 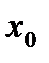, если существует такая окрестность точки 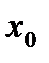, в которой функция имеет все производные до порядка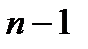 
включительно и, кроме того, в точке 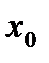существует 
.
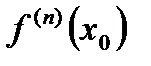ЗАДАЧА І. Пусть функция 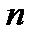раз дифференцирована в точке 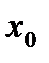. Существует ли такой многочлен 
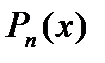степени 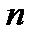, что имеет место соотношения, аналогичное (2):
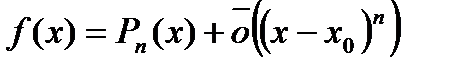, когда 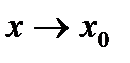, (3)
и если он существует, надо его построить.
Лемма 1. Пусть функция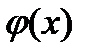 
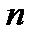раз дифференцирована в точке 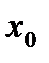и
,
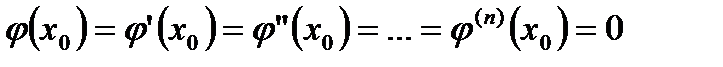тогда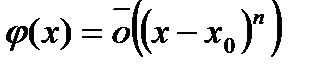 
, когда .
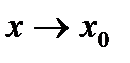Теперь ЗАДАЧУ І можно переформулировать следующим образом.
Пусть функция 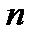раз дифференцирована в точке 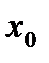. Можно ли найти многочлен 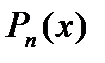степени 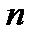такой, чтобы выполнялись условия:
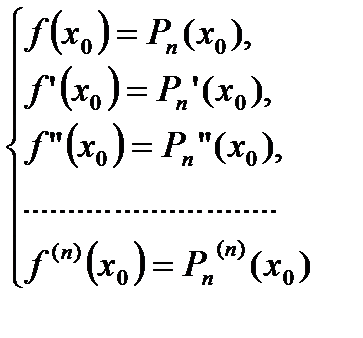(4)
Если мы найдем такой многочлен 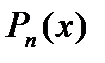, то функция 
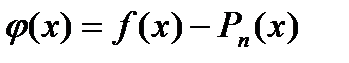будет удовлетворять всем условиям леммы 1:
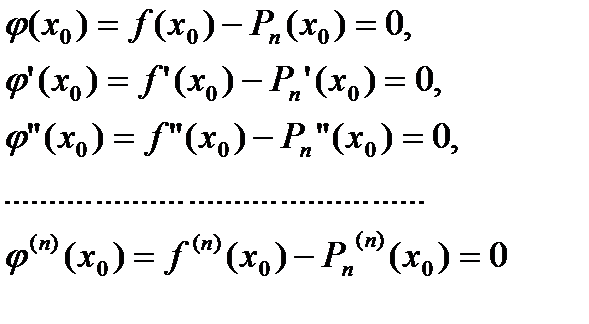
и тогда
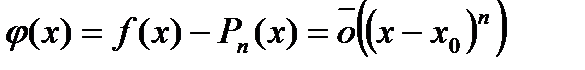, когда ,
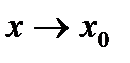откуда 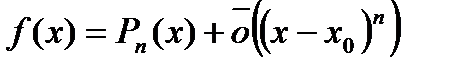, когда .
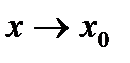Таким образом, многочлен, который удовлетворяет условиям (4), дает решение ЗАДАЧИ І.
Многочлен 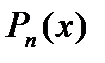будем искать в виде:
.
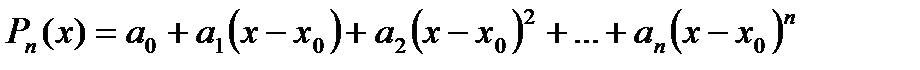Необходимо выбрать коэффициенты многочлена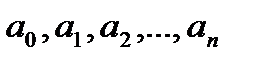 
так, чтобы выполнялись условия (4). Пусть 
:
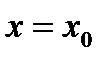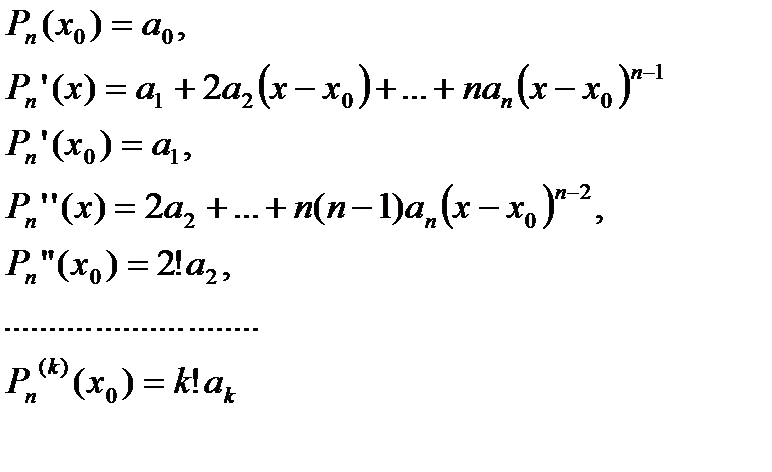
Таким образом, учитывая (4):
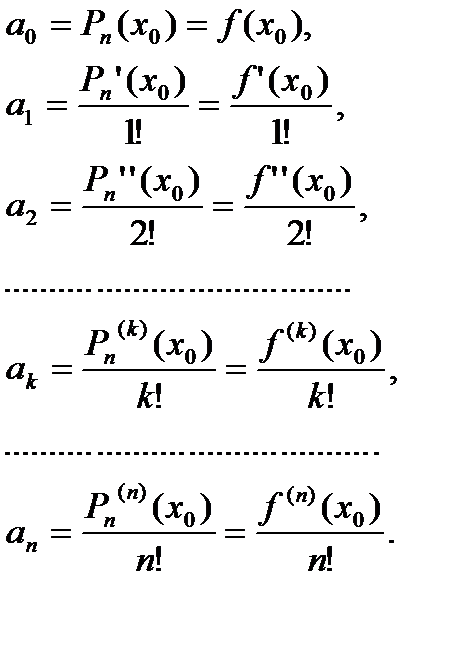
Таким образом искомый многочлен
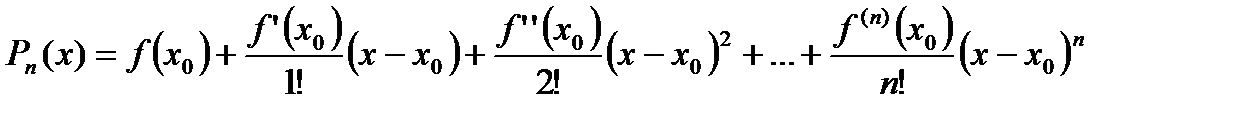. (5)
Многочлен (5) решает ЗАДАЧУ І и называется многочленом Тейлора для функции с центром в точке 
.
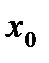Мы доказали
Теорему 4. Пусть функция 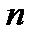раз дифференцирована в точке 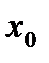, тогда имеет место соотношение:
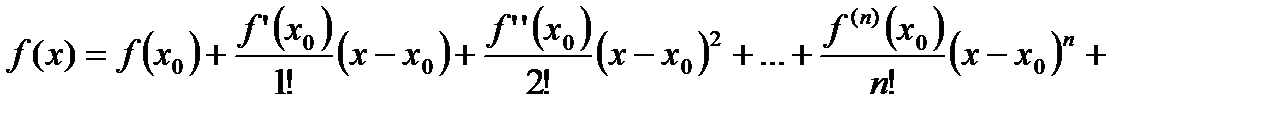
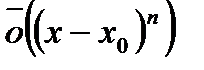, (6)
когда .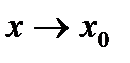
Формула (6) называется формулой Тейлора с остаточным членом в форме Пеано.
Если в формуле (5)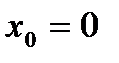 
, то соответствующий многочлен Тейлора называется многочленом Маклорена, а соответствующая формула (6) называется формулой Маклорена.
Теорема 5. Пусть функция 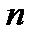раз дифференцирована в точке 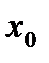, тогда для нее существует единственный многочлен Тейлора с центром в точке .
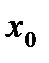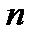Теорема 6 (формула Тейлора с остаточным членом в форме Лагранжа). Пусть функция имеет производную -го порядка, непрерывную на 
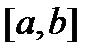, и пусть существует конечная 
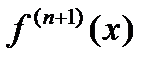в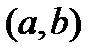 
, тогда 
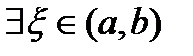такая, что
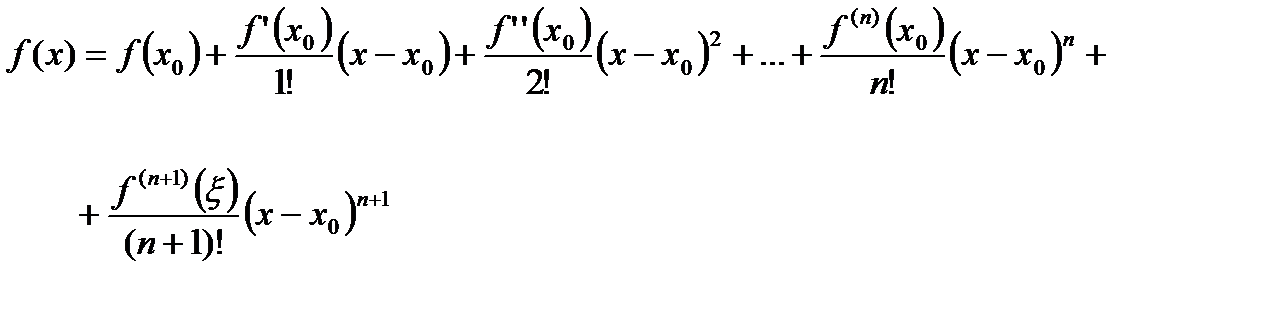, (7)
где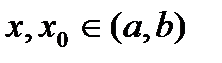 
.
Формула (7) называется формулой Тейлора с остаточным членом в форме Лагранжа.
Вопросы
1. В каких случаях можно использовать правило Лопиталя?
2. Что можно сказать о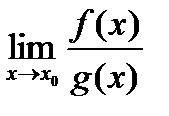 
, если 
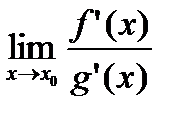не существует?
3. Какая функция называется постоянной? Привести примеры постоянных функций.
4. Доказать критерий постоянства функции.
5. Какая функция называется монотонной, строго монотонной? Привести примеры монотонных функций.
6. Может ли функция одновременно быть монотонно возрастающей и монотонно убывающей? Привести примеры.
7. Доказать критерий монотонности функции.
8. Пусть функция строго монотонно убывает на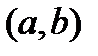 
. Что можно сказать о знаке ее производной на этом интервале? Почему?
9. Пусть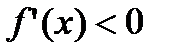 
на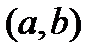 
. Что можно сказать о монотонности функции?
10. Что означает, что функция 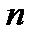раз дифференцирована в точке 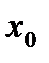? Привести примеры таких функций.
11. Пусть функция 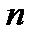раз дифференцирована в точке 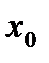. Как она может быть представлена в достаточно малой окрестности ?
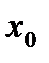12. Определение многочлена Тейлора, многочлена Маклорена.
13. Формула Тейлора с остаточным членом в форме Пеано.
14. Формула Тейлора с остаточным членом в форме Лагранжа.