Вопр. 17.(Расчет трехшарнирных систем).

Рациональное очертание оси арки

Рациональной осью трёхшарнирной арки заданного пролёта и заданной стрелы подъёма называется такая ось, при которой требуемые условиями прочности поперечные сечения арки будут наименьшими. Очевидно, что наименьшая величина нормального напряжения, согласно выражению (3.11), будет в том случае, когда значение изгибающего момента в сечении будет равно нулю. Последнее же возможно в том случае, когда равнодействующая внутренних проходит через центр тяжести поперечного сечения арки. Этому условию должны удовлетворять все сечения арки.

Рассмотрим типичный случай загружения, когда арка находится под действием равномерно распределённой нагрузки (рис. 3.17).

Исходя из определения рациональной оси арки приравняем к нулю выражение (3.5).

Из этого выражения следует:

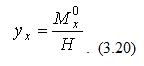
Неразрезные балки. Уравнения трех моментов для расчета неразрезных балок получены благодаря удачному выбору основной системы: При использовании этих уравнений очень важно помнить, при каком направлении опорных моментов они выведены. Без этого при решении задач нельзя будет правильно учесть, знаки полученных неизвестных Необходимо обратить внимание на использование уравнений трех моментов при наличии загруженной консоли и в случае заделки одного или обоих концов.

Рассмотрим частный случай, когда замковый шарнир С расположен в середине пролёта арки. Величина балочного изгибающего момента, как известно, может быть определена из выражения

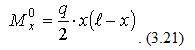
Распор Н для симметричного расположения замкового шарнира будет соответственно равен:

Подставляя (3.21) и (3.22) в выражение (3.20), получим выражение, описывающее рациональное очертание оси арки, загруженной равномерно распределённой нагрузкой интенсивностью q, при расположении замкового шарнира в середине пролёта арок

После арифметических преобразований выражения (3.23) получим выражение, описывающее рациональное очертание оси арки.

Анализ выражения (3.24) свидетельствует о том, что в данном частном случае нагружения трёхшарнирной арки рациональной оказалась ось, описанная по квадратной параболе.

Аналогичным методом можно вывести любую формулу, описывающую рациональное её очертание в зависимости от характера внешнего нагружения. Однако, как показывает опыт, технологически осуществить такие конструкции практически невозможно.

Вопр. 18. АРКА С ЗАТЯЖКОЙ — арка, пяты или ветви которой соединены затяжкой для восприятия распора

Двухшарнирные арки с затяжкой

За основную систему может быть принята криволинейная балка с перерезанной затяжкой (рис. 2, б). Взаимное смещение сечений разреза затяжки для основной системы равно нулю, поэтому каноническое уравнение метода сил имеет вид:

(12)

где δ11 – взаимное смещение сечений разреза по направлению силы Х1 от действия силы Х1 = 1; Δ1F – то же, от внешней нагрузки.

Выражение для Δ1F бу-дет то же, что и для аналогичной двухшарнирной арки (7) или (11). Для перемещения δ11 добавляется влияние удлинения затяжки длиной l в состоянии Х1 = 1:

,

где ЕзАз – жесткость затяжки на растяжение. Следовательно, будем иметь

(13)

и тогда (14)

Распор в двухшарнирной арке с затяжкой будет всегда меньше, чем распор в двухшарнирной арке, так как знаменатель формулы (14) всегда будет больше знаменателя формулы (2).

. Расчетная схема. Понятие о стержневой системе При расчете реального сооружения рассматривают его идеализированную, упрощенную схему, в которой отражаются только его основные свойства. Такая схема называется расчетной. В расчетную схему сооружения вводят идеализированные опоры. Переход к расчетной схеме является необходимой идеализацией реального сооружения. По мере накопления новых результатов испытаний сооружений совершается переход от одной расчетной схемы к другой, более точно отражающей реальное поведение конструкции. В данном издании, кроме пункта 3.2, мы будем рассматривать любое сооружение как плоское, состоящее из стержней соединенных между собой и основанием идеальными связями. Другими словами, в отличие от курса "Сопротивление материалов", мы будем рассматривать не один стержень, а ансамбль стержней, образующих расчетную схему. Ансамбль стержней, соединенных между собой идеальными связями и могущий сопротивляться действию внешней нагрузки, будем называть стержневой системой.

исследовать геометрическую неизменяемость стержневых систем; строить эпюры и линии влияния силовых факторов от статических и подвижных нагрузок; определять усилия в элементах решетки ферм; определять невыгоднейшее положение нагрузки на сооружении; использовать теорию матриц для расчета статически определимых балок и рам; строить линии влияния для элементов решетки в простых и шпренгельных фермах, определять по ним внутренние усилия;

Вопр. 20. Линии влияния внутренних усилий строятся на основе линий влияния моментов и поперечных сил в сечениях простых балок

Вопр. 21. Из всех возможных состояний равновесия системы, подверженной воздействию внешних сил, соответствует то, при котором полная энергия системы принимает стационарная значение. Использование этого вариационного принципа позволяет вывести теорему Лагранжа, согласно которой для линейных систем частная производная от потенциальной энергии деформации по обобщенному перемещению равна соответствующей ему обобщенной силе.

Вопр. 22. Формулой Мора в приведенном виде можно пользоваться для определения перемещений системы, вызванных действием температуры. Если верхнее волокно элемента стержня нагрето на t1, а нижнее – на t2 градусов Цельсия.

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Если отрезок является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле

Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной

Вопр 23. Перемещения, вызванные изменением температуры

Перемещения в сооружениях рубленных домов и бань вызываются не только внешними силами, но и температурным воздействием. Так как в статически неопределимых системах усилия возбуждаются только вследствие сооружения, то в дальнейшем будем рассматривать лишь действие приращений температуры. Температурные перемещения в статически определимых изотропных системах совершаются свободно и, следовательно, не возбуждают усилий. При равномерном нагревании прямолинейного стержня (одинаковое приращение температуры по высоте сечения) он удлиняется без осевых напряжений. Абсолютное удлинение при этом будет alAt, где а — температурный коэффициент линейного расширения.

Вопр 30.

(Метод предельного равновесия). При расчете конструкций по методу предельного равновесия предполагается двухстадийный характер деформирования материала: в первой стадии материал подчиняется закону Гука, пока напряжения не достигнут предела текучести; а затем во второй стадии, предполагая, что в нем в определенной стадии нагружения в опасных сечениях беспредельно развиваются пластические деформации при постоянном напряжении. С появлением пластических деформаций нарушается линейная зависимость между напряжениями и деформациями по закону Гука, и все расчетные формулы, вывод которых основан на этой зависимости, становятся неприменимыми. Нарушается прямая пропорциональность между действующими на элемент конструкции нагрузками и возникающими в нем напряжениями и деформациями. Становится неприменимым один из основных принципов сопротивления материалов – принцип независимости действия сил. Суть метода состоит в том, что конструкция рассматривается в момент, непосредственно предшествующий ее разрушению, когда еще выполняются условия равновесия для внутренних и внешних сил, достигающих предельных значений. Отсюда и произошло название метода предельного равновесия.

Для выполнения расчетов на прочность по методу предельного равновесия вводятся понятия коэффициента запаса прочности и эффективное напряжение.

Коэффициент запаса при данном напряженном состоянии это число, показывающее во сколько раз следует одновременно увеличить все компоненты тензора напряжений, чтобы оно стало предельным.

Эквивалентное напряжение - это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно с заданным.

Для пластичных материалов критерием наступления предельного состояния принимается состояние, при котором максимальные касательные напряжения достигают некоторого предельного значения:

Ϭ_экв=2τ_max=Ϭ₁-Ϭ₃ (1)

Гипотеза максимальных касательных напряжений, приемлемая для пластичных материалов, обнаруживает заметные погрешности для материалов, имеющих различные механические характеристики при сжатии и растяжении.

В таких случаях применяется энергетическая гипотеза, согласно которой предельное состояние в точке наступает тогда, когда энергия формоизменения:

U_пр=((1+µ)/6E)*[(Ϭ₁-Ϭ₂)²+(Ϭ₂-Ϭ₃)²+(Ϭ₃-Ϭ₁)²](2)

принимает некоторое заранее заданное значение. Это предельное значение для U_пр определяется следующим образом. Для простого растяжения выражение (2) принимает вид:

U_пр=((1+µ)/6Е)*2Ϭ²

В сложном напряженном состоянии U_пр принимает значение:

U_пр=((1+µ)/6Е)*2Ϭ²_экв(3)

При совместном рассмотрении (2) и (3) получим:

Ϭ_экв= *[(Ϭ₁-Ϭ₂)²+(Ϭ₂-Ϭ₃)²+(Ϭ₃-Ϭ₁)²]

Следует помнить, что расчет по методу предельного равновесия можно выполнять только для элементов конструкций, изготовленных из пластичных материалов, допускающих пластические деформации в наиболее напряженных точках без появления в них трещин. Недопустимо появление пластических деформаций в деталях машин, длительно работающих при переменных, циклических напряжениях, так как при этом резко снижается число циклов до разрушения, т.е. долговечность детали.