Исходные ряды динамики сглаживаются с помощью трехчленной скользящей средней по формуле:
У ск i = (У i + У i+1 + У i+2) / 3, (6)
где У ск i – сглаженный по скользящей средней уровень ряда (i=1, 2,…)
У i , У i+1 , У i+2 – уровни исходного ряда.
Сглаженных точек получается меньше, так как исчезают уровни в начале и конце ряда. Для их восстановления применяют эмпирические формулы:
У-1= (5У1+ 2 У2 - У3 ) / 6, (7)
У+1 = (- У10 + 2У11 + 5У12 ) / 6, (8)
где У-1 и У+1 - крайняя левая и крайняя правая точки ряда, соответствующие данным за январь и декабрь;
У1, У2,У3,У10, У11, У12 –исходные данные за январь, февраль, март, октябрь, ноябрь и декабрь соответственно.
Сглаживание по среднему абсолютному приросту и среднему коэффициенту роста проводится по формулам:
У∆ i = У1 + 
* (i -1), (9)
Ук i = У1 *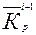 
, (10)
где У∆ i – сглаженный по среднему абсолютному приросту i -й уровень ряда;
Ук i – сглаженный по среднему коэффициенту роста i -й уровень ряда;
– средний абсолютный прирост ряда динамики;
– средний коэффициент роста ряда динамики.
Средний абсолютный прирост рассчитывается по формуле:
= (Уn - У1) / (n-1), (11)
Средний коэффициент роста равен:
= 
= 
(12)
Сглаживание ряда динамики методом наименьших квадратов (МНК) или аналитическим методом проводят на основе подбора теоретической линии регрессии, для которой достигается:
å (У сгл.i - У i) 2 = min. (13)
Если теоретическая линия регрессии – прямая вида У сгл.i = А + В * t i,
то коэффициенты регрессии А и В определяют из системы уравнений:
n*А + В å t i = å У i
A å t i + B å t i 2 = å У i t i , (14)
где n – число точек исходного ряда динамики.
Решение системы уравнений (14) можно упростить, введя для каждого квартала условные обозначения интервалов времени t усл., так чтобы å t усл. = 0.
Система (14) при å t усл. = 0 сводится к более простой
n * А = å У i
B å t 2 i усл = å У i t i усл, (15)
где n – число уровней ряда динамики У i при i=1,2,…, n.
Таким образом, для сглаживания ряда динамики с четным количеством уровней/точек методом наименьших квадратов (МНК) целесообразно построить вспомогательную таблицу 3. Ниже приведен пример для исходного ряда динамики, имеющего четыре уровня.
Таблица 3 – Аналитическое сглаживание (сглаживание методом МНК)
Коэффициенты регрессии А и В определены из системы уравнений:
4 * А = 80
B * 20 = 56 (16)
Откуда А = 20, В = 2,8.
В вышеприведенной таблице сглаженные уровни У сгл.i для каждого i-го периода получены на основе расчетов У сгл.i = А + В * t усл i. Получим уравнение У сгл.i = 20 + 2,8 * t усл i.
Подставив в него значения t усл i , соответствующие каждому кварталу, найдем значения У сгл.i, сглаженные методом МНК.
Для первого квартала t усл i = -3, поэтому У сгл.t= -3 = 20 + 2,8 *(-3) = 11,6. Аналогично рассчитываются сглаженные значения ряда динамики для остальных кварталов.
Выводыо преимуществах и недостатках каждого метода сглаживания можно сделать, ответив на следующие вопросы: какой метод проще (сложнее), какой лучше отражает динамику исходного ряда динамики, какие методы позволяют составить прогноз развития изучаемого явления.