Задача 49. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения директрис эллипсов:
1)  ;
| 3)  ;
|
2)  ;
| 4)  .
|
Задача 50. Составить каноническое уравнение эллипса, зная, что:
1) его полуоси равны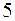 
и 2;
2) его большая ось равна 10, а расстояние между фокусами равно 8;
3) его малая ось равна 24, а расстояние между фокусами равно 10;
4) расстояние между фокусами равно 6, эксцентриситет 
;
5) его большая ось равна 20, эксцентриситет ;
6) его малая ось равна 6 и точка 
принадлежит эллипсу;
7) расстояние между его директрисами равно 5, а расстояние между фокусами равно 4;
8) его большая ось равна 8, а расстояние между его директрисами равно 16;
9) его малая ось равна 6, а расстояние между его директрисами равно 13;
10) расстояние между его директрисами равно 32, а эксцентриситет равен 
;
11) он проходит через точку 
и эксцентриситет равен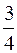 
;
12) он проходит через точку 
и её расстояние от левого фокуса равно 20.
Задача 51. Найти точки эллипса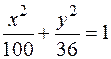 
, расстояние которых до правого фокуса равно 14.
Задача 52. Найти точки эллипса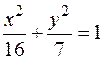 
, расстояние которых до левого фокуса равно 2,5.
Задача 53. Найти длину хорды эллипса, которая делит пополам угол между осями, если:
1) 
;
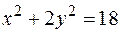2) .
Задача 54. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса .
Задача 55. Составить уравнение прямой, проходящей через правый фокус и верхнюю вершину эллипса 
.
Задача 56*. На эллипсе 
найти точку, расстояние которой от правого фокуса в два раза меньше чем её расстояние от левого фокуса.
Задача 57*. Дан эллипс и окружность, имеющая центр в верхней вершине малой оси эллипса и проходящая через его фокусы. Найти точки пересечения эллипса и окружности.
Гипербола
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний, которых от двух фиксированных точек, называемых фокусами гиперболы, есть величина постоянная (
), меньшая чем расстояние между фокусами (
) (Рис. 11).
Простейшее (каноническое) уравнение гиперболы мы получим, если выберем прямую, соединяющую фокусы, за ось абсцисс и поместим начало координат в середине между ними. Тогда уравнение гиперболы примет вид:
, (21)
где
. (22)
Точки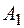 
, 
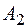, пересечения эллипса с осью называются вершинами гиперболы. Отрезок 
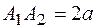называется действительной осью гиперболы, отрезок 
называется мнимой осью гиперболы, параметры 
и 
, входящие уравнение (21), называются действительной и мнимой полуосями соответственно.
Гиперболы
и 
,
называется сопряжёнными.
Если 
, то гипербола называется равносторонней.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к его большой оси, т. е.
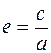. (23)
Очевидно, что 
.
Гипербола (24) состоит из двух бесконечных ветвей (правой и левой). Расстояние точки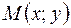 
гиперболы от его фокусов (фокальные радиус-векторы) определяются формулами:
Директрисами эллипса называются две прямые, перпендикулярные большой оси эллипса и отстоящие от его центра на расстоянии, равном 
. Уравнения директрис:
, 
. (24)
Прямые 
называются асимптотами гиперболы.
Задача 58. Составить каноническое уравнение гиперболы, зная, что уравнения асимптот 
и расстояние между директрисами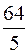 
.
Решение. Каноническое уравнение гиперболы (21):
.
Для того чтобы найти параметры и составим систему.
Известно, что асимптоты гиперболы задаются уравнениями
.
Тогда из условия задачи получим первое уравнение системы:
.
Так как уравнения директрис (24):
, ,
то из условия задачи
.
Из равенств (22) и (23) следует, что
.
Тогда
.
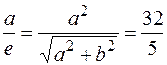Это второе уравнение системы.
Итак, получили систему
Её решение 
, 
.
Искомое уравнение гиперболы
.
Задача 59. Фокусы гиперболы совпадают с фокусами эллипса 
. Составить уравнение гиперболе, если её эксцентриситет равен 2.
Решение. Из канонического уравнения данного эллипса известно, что
, 
.
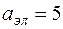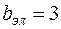По формуле (16) найдём 
:
.
По условию задачи фокусы гиперболы совпадают с фокусами эллипса. Значит
.
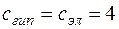Так как эксцентриситет гиперболы равен 2, то
.
Для нахождения 
воспользуемся равенством (22):
.
Следовательно, искомое уравнение гиперболы
.