Нормальное уравнение прямой имеет вид
,
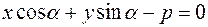где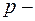 
длина перпендикуляра (нормали), опущенного из начала координат на прямую, 
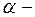угол наклона этого перпендикуляра к оси 
. Чтобы привести общее уравнение прямой 
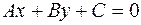к нормальному виду, нужно обе части равенства (12) умножить на нормирующий множитель 
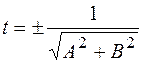, взятый со знаком противоположным знаку свободного члена 
.
Расстояние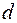 
точки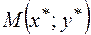 
от прямой найдём по формулам
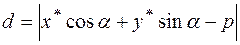
или
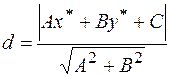. (9)
Уравнение биссектрис углов между прямым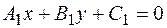и 
и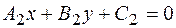 
:
.
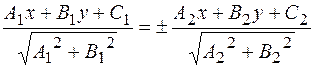Задача 16. Дана прямая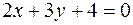 
. Составить уравнение прямой, проходящей через точку 
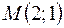параллельно данной прямой.
Решение. По условию параллельности прямых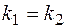 
. Для решения задачи будем использовать уравнение прямой, проходящей через данную точку 
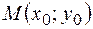в данном направлении (8):
.
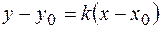Найдём угловой коэффициент данной прямой. Для этого от общего уравнения прямой (5) перейдём к уравнению с угловым коэффициентом (6) (выразим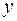 
через 
):
.
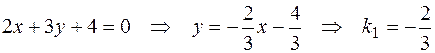Следовательно,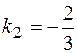 
.
Тогда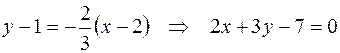 
.
Задача 17. Найти точку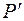 
, симметричную точке 
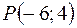, относительно прямой 
.
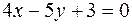Решение. Для того, чтобы найти точку симметричную точке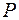 
относительно прямой 
(Рис.7) необходимо:
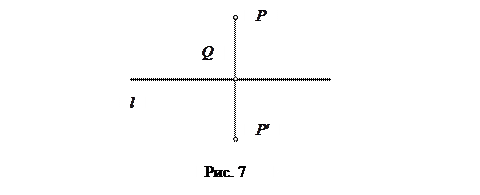
1) опустить из точки 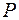на прямую перпендикуляр,
2) найти основание этого перпендикуляра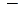 
точку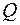 
,
3) на продолжении перпендикуляра отложить отрезок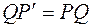 
.
Итак, запишем уравнение прямой, проходящей через точку 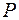перпендикулярно данной прямой. Для этого воспользуемся уравнением прямой, проходящей через данную точку в данном направлении (8):
.
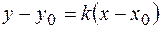Подставим координаты точки :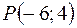
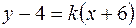. (11)
Угловой коэффициент найдём из условия перпендикулярности прямых:
.
Угловой коэффициент данной прямой
,
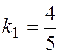следовательно, угловой коэффициент перпендикулярной прямой
.
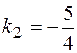Подставим его в уравнение (11):
|
|
.
Далее, найдём точку 
точку пересечения данной прямой и ей перпендикулярной прямой. Так как точка принадлежит обеим прямым, то её координаты удовлетворяют их уравнениям. Значит, для отыскания координат точки пересечения требуется решить систему уравнений, составленную из уравнений этих прямых:
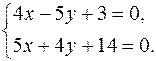
Решение системы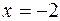 
, 
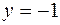, т. е. 
.
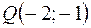Точка 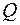является серединой отрезка 
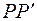, тогда из формул (4):
, 
,
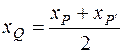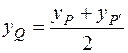найдём координаты точки :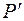
, 
.
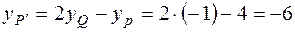Таким образом, искомая точка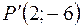 
.
Задача 18. Составить уравнение прямой, которая проходит через точку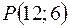 
и отсекает от координатного угла треугольник с площадью, равной 150 кв.ед. (Рис.8).
Решение. Для решения задачи будем использовать уравнение прямой «в отрезках» (7):
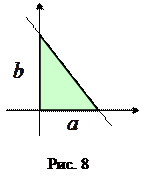
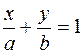. (12)
Так как точка 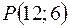лежит на искомой прямой, то её координаты должны удовлетворять уравнению этой прямой:
.
Площадь треугольника, отсекаемого прямой от координатного угла вычисляется по формуле:
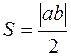
(записан модуль, так как 
и 
могут быть отрицательными).
Таким образом, получили систему для отыскания параметров и :
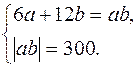
Эта система равносильна двум системам:
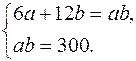
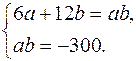
Решение первой системы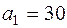 
, 
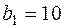и 
, 
.
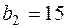Решение второй системы 
, 
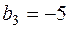и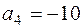 
, 
.
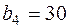Подставим найденные значения в уравнение (12):
, 
, 
, 
.
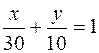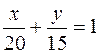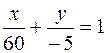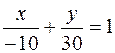Запишем общие уравнения этих прямых:
, 
, 
, 
.
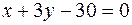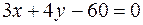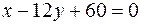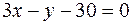Задача 19. Вычислить расстояние между параллельными прямым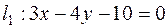и 
и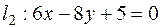 
.
Решение. Расстояние между параллельными прямыми равно расстоянию произвольной точки одной прямой до второй прямой.
Выберем на прямой 
точку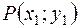 
произвольно, следовательно, можно задать одну координату, т. е. например 
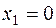, тогда 
.
Теперь найдём расстояние точки 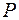до прямой 
по формуле (10):
.
|
.|
|
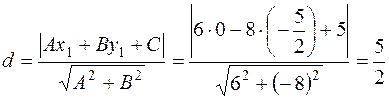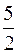Задача 20. Найти уравнение прямой, проходящей через точку пересечения прямых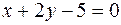 
и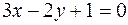 
(не находя точки пересечения) и
1) проходящей через точку 
;
2) параллельной прямой 
.
Решение. 1) Запишем уравнение пучка прямых с известными образующими (9):
.
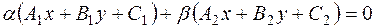Тогда искомая прямая имеет уравнение
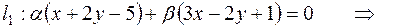
. (13)
Требуется найти такие значения 
и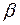 
, при которых прямая пучка пройдёт через точку , т. е. её координаты должны удовлетворять уравнению (13):
.
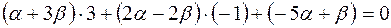Отсюда
.
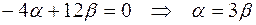Подставим найденное в уравнение (13) и после упрощении получим искомую прямую:
.
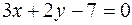2) По условию задачи искомая прямая параллельна прямой
.
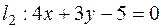Воспользуемся условием параллельности прямых: 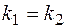. Найдём угловые коэффициенты прямых и . Имеем, что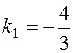 
, 
.
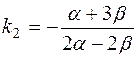Следовательно,
.
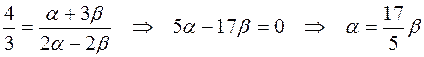Подставим найденное значение в уравнение (13) и упростим, получим уравнение искомой прямой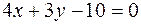 
.