Глава 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Прямоугольная система координат. Простейшие задачи аналитической геометрии на плоскости
Прямоугольная система координат.
Прямая, на которой выбрано положительное направление называется осью.
Прямая, на которой выбрано направление, точка  начало отсчёта и единичный отрезок, называется координатной осью (Рис. 1).
начало отсчёта и единичный отрезок, называется координатной осью (Рис. 1).

Рис. 1.
Координатой любой точки  данной прямой (в установленной системе координат) называется число
данной прямой (в установленной системе координат) называется число 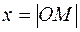 , если направление от начала координат
, если направление от начала координат 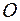 к точке
к точке  совпадает с положительным направлением оси, и
совпадает с положительным направлением оси, и 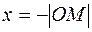 , в противном случае. Обозначение
, в противном случае. Обозначение
 .
.
Две взаимно перпендикулярные координатные оси, с общим началом и равными единичными отрезками, называются прямоугольной декартовой системой координат (ПДСК). Одна из осей (горизонтальная) называется осью абсцисс  , вторая (вертикальная)
, вторая (вертикальная)  осью ординат
осью ординат  .
.
 Плоскость, на которой введена ПДСК, называется координатной плоскостью.
Плоскость, на которой введена ПДСК, называется координатной плоскостью.
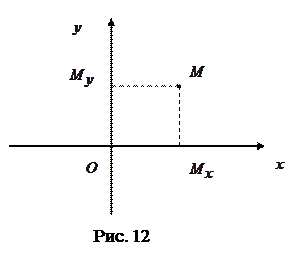
Пусть 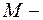 произвольная точка плоскости, опустим из точки
произвольная точка плоскости, опустим из точки  перпендикуляры на оси координат, получим точки
перпендикуляры на оси координат, получим точки 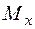 и
и 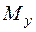 соответственно (Рис. 2).Пусть точка
соответственно (Рис. 2).Пусть точка 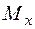 имеет координату
имеет координату  на оси абсцисс, точка
на оси абсцисс, точка 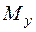 координату
координату 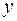 на оси ординат, тогда будем говорить, что точка
на оси ординат, тогда будем говорить, что точка  имеет координаты
имеет координаты  ,
, 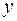 и обозначать
и обозначать
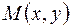
Прямоугольными декартовыми координатами точки  плоскости называется упорядоченная пара действительных чисел
плоскости называется упорядоченная пара действительных чисел  и
и 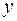 .
.
Расстояние между двумя точками.
Расстояние между точками 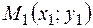 и
и 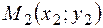 вычисляется по формуле:
вычисляется по формуле:
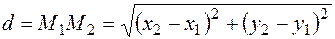 . (1)
. (1)
3. Деление отрезка в данном отношении.
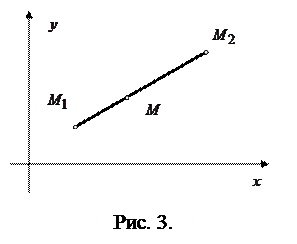
Пусть на плоскости дан произвольный отрезок 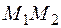 и пусть
и пусть 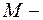 любая точка этого отрезка, отличная от точки
любая точка этого отрезка, отличная от точки 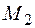 (Рис. 3).
(Рис. 3).
 Число
Число 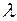 , определяемое равенством
, определяемое равенством
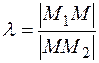 , (2)
, (2)
называется отношением, в котором точка  делит отрезок
делит отрезок 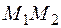 .
.
|
|
Координаты точки 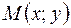 по данному отношению
по данному отношению 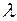 и данным координатам точек
и данным координатам точек 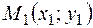 и
и 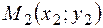 можно найти по формулам
можно найти по формулам
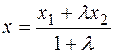 ,
, 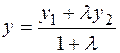 . (3)
. (3)
В частности, при делении отрезка пополам, т. е. при 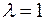 , получаем формулы для нахождения координат середины отрезка:
, получаем формулы для нахождения координат середины отрезка:
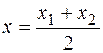 ,
, 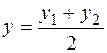 . (4)
. (4)
Используя равенства (3) можно получить формулы для нахождения координат точки пересечения медиан треугольника  , если
, если 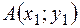 ,
, 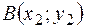 ,
, 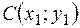 :
:
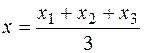 ,
,  .
.
Площадь треугольника.
Площадь треугольника с вершинами 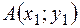 ,
, 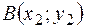 ,
, 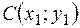 равна:
равна:
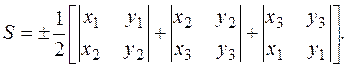
Выражение вида 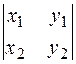 равно
равно 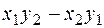 и называется определителем второго порядка.
и называется определителем второго порядка.
Задача 1. Найти точку, удалённую на 13 единиц, как от точки 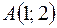 , так и от оси
, так и от оси  .
.
Решение. Пусть 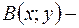 искомая точка. Так как точка
искомая точка. Так как точка  удалена от оси
удалена от оси  на 13 единиц, то её абсцисса
на 13 единиц, то её абсцисса 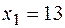 или
или 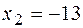 . Следовательно, получим две точки
. Следовательно, получим две точки 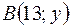 и
и 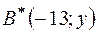 . Найдём вторую координату.
. Найдём вторую координату.
По условию задачи, расстояние 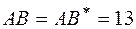 . По формуле (2) имеем,
. По формуле (2) имеем,
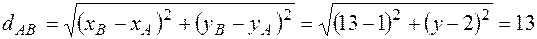 ,
,
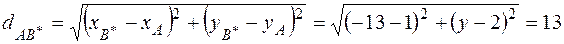 .
.
Возведем в квадрат обе части равенств:
 ,
,
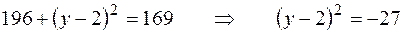 (невозможно).
(невозможно).
Отсюда,
 или
или 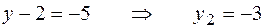 .
.
Таким образом, получили две точки 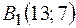 и
и 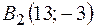 .
.
Задача 2. Даны три вершины параллелограмма 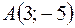 ,
, 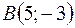 ,
, 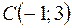 . Определить четвёртую вершину
. Определить четвёртую вершину 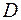 , противоположную
, противоположную  .
.
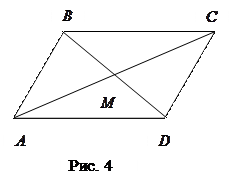
Решение. Пусть 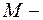 точка пересечения диагоналей данного параллелограмма (Рис. 4) Тогда по свойству параллелограмма, она делит его диагонали пополам, т. е.
точка пересечения диагоналей данного параллелограмма (Рис. 4) Тогда по свойству параллелограмма, она делит его диагонали пополам, т. е. 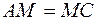 и
и 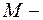 середина
середина  . Из (4)
. Из (4)
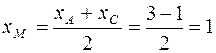 ,
,
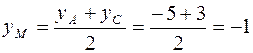 ,
,
Таким образом, точка 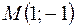 . Аналогично,
. Аналогично,  является серединой диагонали
является серединой диагонали 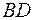 . Так как
. Так как
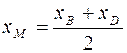 ,
, 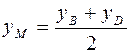 ,
,
то имеем,
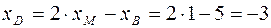 ,
,  .
.
Итак, четвёртая вершина параллелограмма 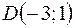 .
.
Задача 3. Даны вершины треугольника 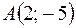 ,
, 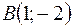 ,
, 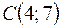 . Найти длину его медианы
. Найти длину его медианы 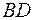 и биссектрисы
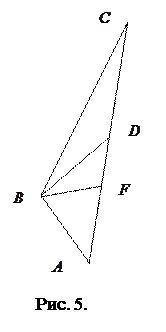
и биссектрисы 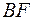 (Рис.5).
(Рис.5).
Решение. Пусть 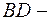 медиана треугольника
медиана треугольника  . Тогда из определения медианы следует, что точка
. Тогда из определения медианы следует, что точка 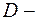 середина отрезка
середина отрезка  . Вычислим координаты точки
. Вычислим координаты точки 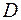 , используя формулы (4):
, используя формулы (4):
|
|
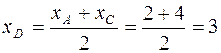 ,
,
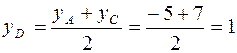 .
.
Итак, точка 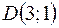 .
.
Найдём длину медианы по формуле расстояния между двумя точками (2):
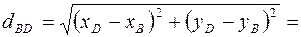
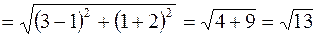 .
.
Таким образом, длина медианы 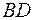 равна
равна 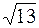 .
.
Пусть 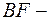 биссектриса внутреннего угла треугольника
биссектриса внутреннего угла треугольника  при вершине
при вершине  . Воспользуемся следующим свойством биссектрисы треугольника: биссектриса делит противолежащую сторону в отношении пропорциональном прилежащим сторонам, т. е.
. Воспользуемся следующим свойством биссектрисы треугольника: биссектриса делит противолежащую сторону в отношении пропорциональном прилежащим сторонам, т. е.
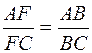 .
.
Вычислим длины сторон  и
и 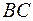 по формуле (2):
по формуле (2):
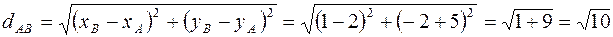 ,
,
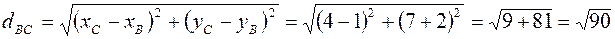 .
.
Таким образом,
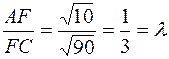 .
.
Координаты точки 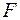 определим по формулам (3):
определим по формулам (3):
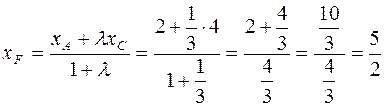 ,
,
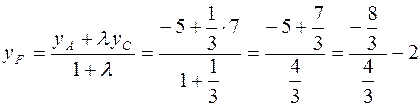 .
.
Итак, точка 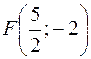 . Найдём длину биссектрисы:
. Найдём длину биссектрисы:
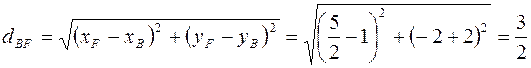 .
.
Задачи для самостоятельного решения.
Задача 4. Где расположены точки имеющие: 1) равные абсциссы;2) равные ординаты; 3) равные координаты.
Задача 5. Определить координаты точки, симметричной точке  относительно оси абсцисс; относительно оси ординат, если 1)
относительно оси абсцисс; относительно оси ординат, если 1) 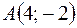 ; 2)
; 2) 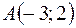 .
.
Задача 6. Построить треугольник  . Доказать, что он прямоугольный, если:
. Доказать, что он прямоугольный, если:
1) 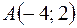 ,
, 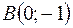 ,
, 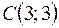 ;
;
2) 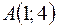 ,
, 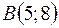 ,
,  .
.
Задача 7. На оси ординат найти точку равноудалённую от точек  и
и  , если:
, если:
1) 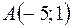 ,
, 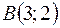 ;
;
2) 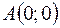 ,
, 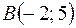 .
.
Задача 8. Найти центр и радиус окружности, описанной около треугольника  , если:
, если:
1)  ,
, 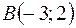 ,
, 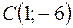 ;
;
2) 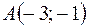 ,
, 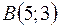 ,
, 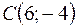 .
.
Задача 9. Даны две смежные вершины параллелограмма  ,
,  и точка пересечения его диагоналей
и точка пересечения его диагоналей  . Определить две другие вершины, если:
. Определить две другие вершины, если:
1) 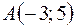 ,
, 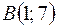 ,
, 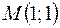 ;
;
2) 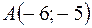 ,
, 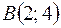 ,
, 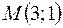 .
.
Задача 10. Отрезок, ограниченный точками  ,
,  , разделён на равные части. Определить координаты точек деления, если:
, разделён на равные части. Определить координаты точек деления, если:
1)  ,
, 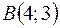 , на три части;
, на три части;
2) 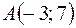 ,
, 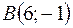 , на четыре части.
, на четыре части.
Задача 11. Дан треугольник  . Найти длину медианы
. Найти длину медианы 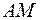 и длину биссектрисы
и длину биссектрисы  , если
, если
1) 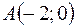 ,
, 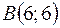 ,
, 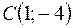 ;
;
2) 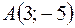 ,
, 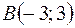 ,
, 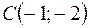 .
.
Задача 12. Вычислить площадь треугольника с вершинами 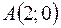 ,
, 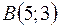 ,
, 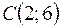 .
.
Задача 13. Показать, что точки лежат на одной прямой 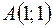 ,
, 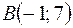 ,
, 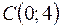 .
.
Задача 14*. Даны две вершины 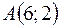 и
и 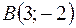 треугольника
треугольника  и точка
и точка 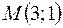 пересечения его медиан. Определить координаты вершины
пересечения его медиан. Определить координаты вершины  .
.
|
|
Задача 15*. Отрезок  разделён точками
разделён точками 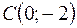 и
и 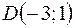 на три равные части. Найти координаты концов отрезка.
на три равные части. Найти координаты концов отрезка.