Для характеристики асимметрии и формы кривой распределения случайной величины служат коэффициент асимметрии и эксцесс.
Коэффициент асимметрии при нормальном распределении равен 0. Он рассчитывается по следующим формулам:
A = L30/S3,
L30 = (1/n-1)*[∑(xi-χ)3].
Для обозначения L30 была использована та же формула, что и для расчета дисперсии, только отклонение от выборочного среднего возводится не в квадрат, а в третью степень. В этом случае, если наше распределение не будет симметричным, то и коэффициент асимметрии A не будет равен 0, то есть мы будем иметь или положительную или отрицательную асимметрию, как показано на рисунке.

Рис. Асимметричные распределения.
Если мы хотим оценить форму кривой распределения, насколько наша вершина кривой распределения острая или сглаженная, то пользуются понятием эксцесса, который рассчитывают по формуле:
Э = L40/S4 - 3,
L40 = (1/n-1)*[∑(xi-χ)4].
Эксцесс нормального распределения равен 0, кривая с более острой вершиной будет иметь положительный эксцесс, а более пологая кривая будет иметь отрицательный эксцесс, как отражено на рисунке. Положительный эксцесс свидетельствует о ненормальном однообразии изучаемой совокупности, а отрицательный эксцесс свидетельствует напротив как раз о ненормальном разнообразии изучаемой совокупности.

Рис. Положительный и отрицательный эксцесс.
Согласно классификации математика Пирсона все результаты измерений природных объектов, имеют распределения, которые можно разделить на три типа. К первому типу можно отнести массивы данных, имеющие симметричное нормальное распределение, ко второму типу относятся массивы данных, которые после математических преобразований будут иметь нормальное распределение и к третьему типу относятся массивы данных, которые при любых преобразованиях не будут иметь нормальное распределение. Одним из самых близких к нормальному распределению является логнормальное распределение, имеющее слабую левую асимметрию и относящееся ко второму по Пирсону типу распределений. Кривая логнормального распределения отражена на рисунке. Существуют две физические причины асимметричности. Первая причина кроется в пороге чувствительности приборов, определяющих концентрацию редких химических элементов (селен, радий и др.). Левая асимметричность возникает, из-за того, что много данных концентрируется около порога чувствительности, и если бы этого порога не было, то распределение приняло бы нормальный симметричный вид.
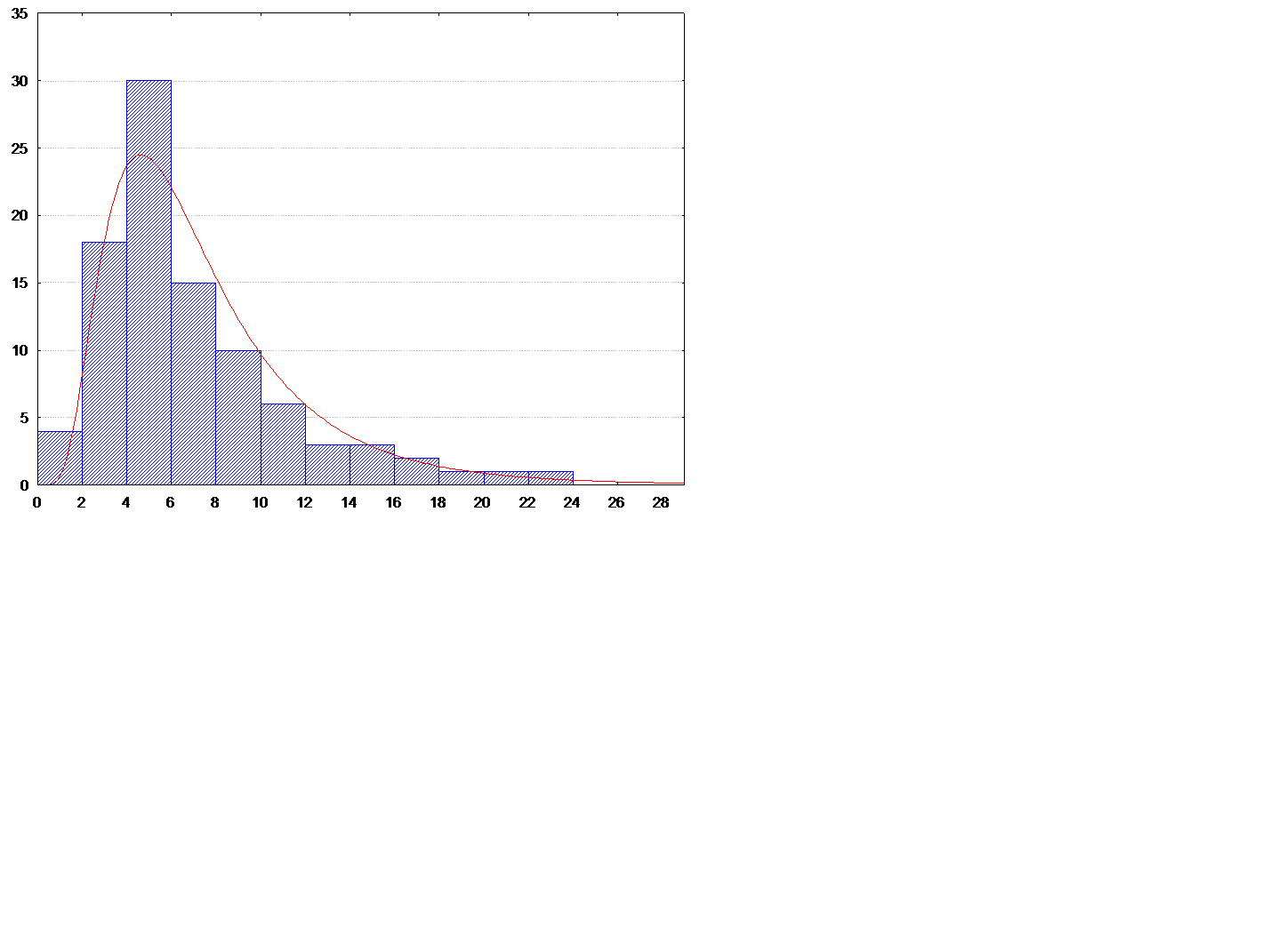
Рис. Кривая логнормального распределения.
Вторая причина кроется в детерминированности изменений природных объектов, тем более мощные геохимические и тектонические процессы, которые протекали при формировании залежей полезных ископаемых, тем более кривая распределения характеристик этих залежей будет асимметричной. Если результаты наблюдений, распределение которых представлено на рисунке, прологарифмировать (то есть вместо переменной xi использовать переменную y = log xi), то распределение прологарифмированной переменной примет нормальный вид. Все перечисленные ранее параметры и статистики также характерны и пригодны и для логнормального распределения. На практике они рассчитываются по тем же формулам, только предварительно все значения выборки логарифмируются, однако основные статистики можно посчитать, используя и не преобразованные данные, в этом случае среднеарифметическому значению будет соответствовать геометрическое среднее, а значению дисперсии будет соответствовать геометрическая дисперсия.
Много массивов данных имеют распределения, которые относятся по классификации Пирсона к третьему типу, в этот тип входит обширная группа асимметричных распределений (в том числе и бета, и гамма распределения). Данные, которые подчиняются этим распределениям, никак не могут быть преобразованы таким образом, чтобы после они имели нормальное распределение. Параметрами гамма - распределения являются величины r и β, первый является параметром положения, а второй параметром масштаба.

Рис Примеры кривых плотности вероятности, соответствующие различным значениям r, при β = 1.
Выбор гамма распределения в качестве модели распределения изучаемой совокупности определяется наличием у наблюдаемой кривой распределения, так называемого хвоста, являющегося следствием асимметричности распределения и препятствующим различным математическим преобразованиям привести экспериментальные данные к нормальному или логнормальному распределению. Характерной особенностью гамма - распределений является сильная зависимость между средним и дисперсией, тогда как в случае нормального распределения такой зависимости нет. Случаи, когда среднее значение и стандартное отклонение изменяются почти одинаково и связаны определенной зависимостью, называется ПРОПОРЦИОНАЛЬНЫМ ЭФФЕКТОМ. Основные компоненты полиметаллических месторождений, месторождений цветных металлов и золота могут подчиняться разновидностям гамма – распределения. Частным случаем, гамма распределений является распределение Пуассона. Особенно это распределение характерно для месторождений золота, так как именно в большей части на этих месторождениях часты находки самородков золота (редкие события) или можно перефразировать - встречаются пробы с аномальным высоким содержанием золота (ураганные пробы), во много раз превышающим наиболее распространенные содержания металла по конкретному месторождению. Несмотря на то, что гамма-бета распределения, в том числе и распределение Пуассона хорошо изучены на практике, специалисты стараются не использовать эту модель для оценки истинных параметров изучаемой совокупности из-за ряда причин, в том числе и из-за сильной зависимости между средним и дисперсией. Для решения этой задачи общепринят иной подход, при котором ураганные пробы стараются нейтрализовать и затем после логарифмирования данных предположить хотя бы логнормальную модель их распределения. Сама проблема ураганных проб предполагает две стадии ее решения, в первую стадию, нужно выявить ураганные пробы, а во вторую стадию их нейтрализовать. Существует много способов регистрации ураганных проб. Однако в последнее время среди специалистов наибольшую популярность получили “квантильный” способ обнаружения ураганных значений металлов в пробах и способ обнаружения ураганных проб по излому на кумулятивной кривой распределения. Эти способы описаны в книге Ю.Е. Капутина “Горные компьютерные технологии и геостатистика”. Если придерживаться терминологии предложенной в этих лекциях, то первый способ можно назвать децильным способом, так как массив проб сначала сортируется по величине содержания металла от минимального до максимального, затем строится частотная таблица и гистограмма. А после таблица разделяется на заданное количество, обычно на 10 частей (то есть массив разделяется на децили). В результате формируется таблица, пример которой приведен ниже.
| Класс | Число записей | Среднее значение | Минимум | Максимум | Доля металла с данным содержанием от всей выборки | Доля металла с данным содержанием от всей выборки (%) |
| 0-10 | 0.004 | 0.000 | 0.010 | 4.805 | 0.07% | |
| 10-20 | 0.010 | 0.010 | 0.018 | 11.522 | 0.16% | |
| 20-30 | 0.021 | 0.018 | 0.030 | 23.816 | 0.34% | |
| 30-40 | 0.035 | 0.030 | 0.049 | 38.823 | 0.55% | |
| 40-50 | 0.052 | 0.049 | 0.060 | 57.571 | 0.82% | |
| 50-60 | 0.080 | 0.060 | 0.100 | 88.946 | 1.27% | |
| 60-70 | 0.128 | 0.100 | 0.160 | 141.922 | 2.02% | |
| 70-80 | 0.219 | 0.160 | 0.290 | 243.590 | 3.47% | |
| 80-90 | 0.426 | 0.290 | 0.640 | 472.534 | 6.73% | |
| 90-100 | 5.370 | 0.640 | 305.310 | 5938.771 | 84.57% | |
| ВСЕГО | 0.633 | 0.000 | 305.310 | 7022.301 | 100.00% | |
| 90-91 | 0.677 | 0.640 | 0.720 | 75.161 | 1.27% | |
| 91-92 | 0.777 | 0.720 | 0.840 | 86.204 | 1.45% | |
| 92-93 | 0.896 | 0.840 | 0.950 | 99.474 | 1.67% | |
| 93-94 | 1.029 | 0.950 | 1.120 | 114.198 | 1.92% | |
| 94-95 | 1.238 | 1.120 | 1.390 | 137.390 | 2.31% | |
| 95-96 | 1.587 | 1.390 | 1.790 | 176.153 | 2.97% | |
| 96-97 | 2.046 | 1.790 | 2.350 | 227.100 | 3.82% | |
| 97-98 | 2.899 | 2.360 | 3.690 | 321.840 | 5.42% | |
| 98-99 | 5.497 | 3.700 | 8.660 | 610.180 | 10.27% | |
| 99-100 | 38.234 | 8.670 | 305.310 | 4091.070 | 68.89% | |
| ВСЕГО | 5.370 | 0.640 | 305.310 | 5938.770 | 100.00% |
Если последний класс (90-100%) содержит долю металла, большую чем 40% от общего количества, то считается, что в массиве данных существуют ураганные пробы. Далее рассчитывается аналогичная таблица для последнего класса. Границей для ураганных проб считается минимальное содержание первого класса, содержащего долю металла более 10%. В данном примере – это 3.7 г/т. Считается, что подобный анализ нужно проводить для каждого типа руд, и для каждого участка месторождения. На практике отмечается много случаев, когда границы ураганных проб на одном и том же месторождении резко отличались друг от друга на разных его участках. Второй способ состоит в том, что строится кумулятивное распределение массива данных, но отображается оно в виде огивы и исследуется конечная часть хвоста распределения. На графике отмечается место перегиба кумулятивной кривой, которое и является границей, после которой фиксируются ураганные пробы.

Рис. Определение границы, после которой фиксируются ураганные пробы по месту излома огивы.
Существуют еще более простые методы выявления ураганных проб, можно например, просто определить ураганные пробы в хвосте массива распределения, после достижения 95% или 99% накопленных частот.
Есть несколько подходов и к нейтрализации ураганных проб.
- Можно исключить аномальные значения из выборки (например, просто отрезать хвост распределения после достижения 95%-99% накопленных частот).
- Можно вместо аномальных значений указать пороговые значения, при которых выборочные данные будут иметь нормальное или логнормальное распределение.
- Можно присвоить аномальным значениям среднеарифметические значения выборки.
Подразумевается, что в первом и третьем случае, после процедур данные будут иметь нормальное или логнормальное распределение. Нейтрализация ураганных проб приводит к разрушению пропорционального эффекта, если после массив данных будет иметь распределение близкое к нормальному. Однако вопрос и о способах выявления и о необходимости нейтрализации ураганных проб остается открытым, так как в любом случае, мы можем допустить еще большую ошибку при оценке истинных параметров, как всей изучаемой совокупности, так и ее частей. Так, например, нейтрализация ураганных проб в выборке, при разведке месторождений золота может уменьшить оценку запасов месторождения, но главное значительно ухудшить экономическую оценку месторождения, из-за высокой цены на этот металл. Тем не менее, большинство специалистов соглашаются, что лучшим выбором для оценки параметров будет выбор нормальной модели распределения для выборочных данных. То есть наши оценки параметров будут более точными, чем ближе к нашему экспериментальному распределению будет подходить нормальная модель распределения. Нейтрализация ураганных проб необходима перед интерполяционными процедурами, распространяющими значение признака на прилегающие пространства, в которых не было произведено опробование.
Обычно мы не знаем, какой вид имеет распределение совокупности, часто по характеру кривой распределения выборки мы предполагаем, что распределение совокупности может значительно отличаться от нормального распределения, часто после любых математических преобразований полученные данные все равно не имеют нормальное распределение. А.М.Ляпунов доказал, что если выборки извлечены случайно из любой совокупности, то средние, вычисленные для этих данных, а именно выборочные средние являются случайными величинами, распределение, которых стремится к нормальному распределению при увеличении объема выборки при условии, что совокупность обладает конечной средней и ограниченной дисперсией. Можно сказать, что это главный тезис теоремы П.Л.Чебышева и А.М.Ляпунова, которая известна под именем – центральная предельная теорема. Предположим, что мы делаем выборку из U-образного распределения. Большая часть наблюдений может быть получена из двух краев распределения, в этом случае при расчете среднеарифметического значения, большие значения погашаются низкими значениями и среднеарифметическое значение находится близко к центру распределения. Если этот эксперимент повторить тысячу раз, то окажется, что выборочные средние будут располагаться всегда ближе к центру U-образного распределения и их распределение будет нормальным. Так как распределение выборочных средних значений стремится к нормальному распределению, то его можно описать двумя статистиками – средним и дисперсией. Из центральной предельной теоремы следуют четыре важных для нас определяющих вывода.
1. Как теоретические, так и эмпирические исследования показали, что среднее значение выборочных средних при увеличении количества данных в выборке будет стремиться к истинному среднему, то есть χχ = μ.
Здесь необходимо более подробно объяснить такое понятие как ошибка выборочного наблюдения или предельная ошибка, в геологической практике это понятие получило название погрешности наблюдения. Ошибкой выборочного наблюдения называется разность между оценкой параметра и истинным его значением.
Δχ = |χ - μ|.
П.Л.Чебышев первый вывод теоремы формулирует таким образом, что при достаточно большом числе независимых наблюдений можно с вероятностью близкой к 1 утверждать, что отклонение средней выборочных средних от истинного среднего будет сколь угодно малой.
2. Дисперсия выборочных средних при увеличении количества данных в выборке стремится к дисперсии совокупности, деленной на объем выборки. Стандартное отклонение выборочных средних значений как корень квадратный из дисперсии выборочных средних в мировой практике принято называть стандартной ошибкой среднего или просто стандартной ошибкой. Она описывает изменчивость, которую можно ожидать при повторных случайных отборах из той же совокупности. В статистической литературе она имеет разные названия, такие как средняя ошибка выборки, относительная ошибка, величина погрешности. П.Л.Чебышев доказал, что величина ошибки выборочного наблюдения или погрешности не должна превышать стандартную ошибку среднего, определяемую по формуле -
SE = σ/√n,
где SE – стандартная ошибка, а σ – истинное стандартное отклонение (стандартное отклонение генеральной совокупности).
Величина стандартной ошибки прямо пропорционально зависит от истинной дисперсии и обратно пропорционально зависит от количества данных в выборке, то есть, увеличивая количество данных наблюдения в выборке, мы можем уменьшить погрешность определения такого параметра как среднее.
3. Зная среднюю величину выборочных средних и стандартную ошибку можно определить границы, внутри которых с большой вероятностью, может быть истинное среднее значение генеральной совокупности. Расстояние между этими границами называется интервалом доверия, или доверительным интервалом. Доверительный интервал определяется по следующей формуле -
1/2 SE - χχ +1/2SE или
1/2 σ/√n - χχ + 1/2 σ/√n.
Так как распределение выборочных средних при большом числе независимых наблюдений стремится к нормальному распределению, то и для определения того, с какой вероятностью истинное среднее - μ может находиться внутри доверительного интервала, также можно применить правило трех σ (правило трех стандартных отклонений). Так как границы интервала доверия определяется плюсом и минусом половины стандартной ошибки, то можно сказать, что истинное среднее – μ находится в доверительном интервале с вероятностью близкой к 68.3%.
Если мы увеличим доверительный интервал и определим его плюсом и минусом из двух стандартных отклонений от среднего выборочных средних, то мы можем сказать, что истинное среднее – μ находится в интервале доверия с большей вероятностью равной 95.4%.
Чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью мы судим о ее величине.
Однако по этой формуле мы не когда не сможем определить не величину погрешности определения среднего, не доверительные границы, так как мы при проведении геологоразведочных работ не знаем истинного стандартного отклонения изучаемой совокупности, а пользуемся только оценкой стандартного отклонения, определяемого по выборочным данныма пользуемся только оценкой ности.работ него не доверительные границы, так как мы не когда не знаем истинного стандартногоостид.
4. Для определения стандартной ошибки и границ доверительного интервала на практике используется оценка стандартного отклонения, рассчитанная по выборочным данным, и в этом случае для определения границ вводится поправка Стьюдента - tα, рассчитанная им для разных степеней свободы и уровня риска. В этом случае окончательная формула определения доверительного интервала и стандартной ошибки или погрешности будет следующей
tα*1/2 S/√n - χχ + 1/2 S/√n *tα.
Значение центральной предельной теоремы очень важное, центральная предельная теорема позволяет сформулировать статистические критерии, основанные на характеристиках нормальной кривой и применять их даже в тех случаях, когда совокупность, из которой взята выборка, не распределена нормально. Если наши экспериментальные данные не подчиняются нормальному распределению, то все равно мы можем оценивать истинные параметры, но не точно, а с погрешностью, в интервалах доверия и, увеличивая количество данных в выборке, мы можем этот интервал доверия сужать, то есть давать более точную оценку параметров. Эти выводы из центральной предельной теоремы являются универсальными и их, возможно, использовать для всех случаев, даже если изначально наши выборочные данные подчиняются и нормальному распределению, так как не обязательно, что изучаемая совокупность будет иметь нормальное распределение. На практике в этом случае часто также используют при определении точности оценок параметров выводы из нормального закона распределения. Если, например, дается оценка среднего содержания, то утверждают, что с вероятностью в 68.3% истинное среднее (или математическое ожидание) - μ находится в пределах плюс - минус в одно стандартное отклонение от выборочного среднеарифметического содержания.
Несомненно, дисперсия является базисной оценкой для определения точности наших оценок. Так, например, при оценке запасов месторождений металлов доминирующим компонентом является колебание металла в нашей выборке, отражающее природную изменчивость изучаемого объекта. Умножив запасы руды, которые мы определили как произведение объема рудного тела на плотность руды, на среднее содержание металла, то мы получим оценку запасов конкретного металла в данном месторождении. Определим стандартную ошибку через коэффициент вариации, и получим значение погрешности в процентах. Это создает удобство для дальнейших расчетов. Например, мы оценили некоторое месторождение золота как крупное с запасами металла в 100 тонн, однако и стандартная ошибка или погрешность определения среднего содержания металла равна по нашим расчетам - 100%. Значит, мы можем определить границы интервала доверия, в котором с вероятностью в 68.2% находится истинное количество золота на этом месторождении. Соответственно если использовать приведенную ранее формулу определения доверительных границ, то, игнорируя поправки Стьюдента, истинное количество металла может находиться в пределах от 50 до 150 тонн, если например погрешность определения среднего содержания металла -50%, то истинное количество металла может находиться в пределах от 75 до 125 тонн.
В программе Datamine Studio для подбора распределения для данных используют процесс HISFIT, наличие на гистограмме несколько вершин может говорить о смешении в одном массиве несколько качественно различных групп данных или узкой ширине интервала столбца гистограммы. В этом случае следует разделить массив на группы и рассчитать гистограммы для каждой группы.
Для достаточно точной оценки взаимосвязи двух компонентов используется корреляционный анализ. Два компонента могут быть некоррелированы, когда рост одного компонента не приводит к устойчивым изменениям другого компонента, положительно коррелированны, если рост значений одного компонента приводит к росту другого компонента, отрицательно коррелированны в обратном случае. Коэффициент корреляции рассчитывается по формуле:
ρ=covx,y/δxδy
Коэффициент корреляции меняется от -1 до +1, чем больше связь, тем этот коэффициент ближе к 1.
Еще один из самых простых методов пространственного анализа данных это регрессионный анализ. К данным, отображенным в виде точек на диаграмме или на графике можно подобрать или линию или кривую, которая бы наиболее близко лежала к точкам данных. Самый простой случай – линейная регрессия, когда данные описываются прямой линией с уравнением

В других случаях используются нелинейные уравнения. Для подбора прямых или кривых используются нормальные уравнения, которые приведены в любом учебнике статистики.

Данные, с которыми приходится иметь дело геологам, непосредственно связаны с пространством, то есть каждая проба имеет пространственные координаты. Положение данных фиксируется в пространстве на планах и разрезах. Уже здесь геологи получают первичную информацию о равномерности опробования, наличии богатых и бедных зон. Более полную информацию несет в себе карта изолиний переменной по значениям в пробах. Анализируя карту изолиний, например полезного компонента можно более определенно выделять зоны с повышенной и пониженной изменчивостью компонента, зоны с более высоким или более низким его содержанием. Однако перед построением самой простой карты изолиний желательно привести пункты наблюдений к равномерному виду, так как иначе мы будем получать значительную ошибку при интерполяции в местах где точек наблюдения меньше. Эту задачу в нашей стране решал Делонэ. Он усовершенствовал метод классической триангуляции, предложив способ построения треугольников для последующего интерполирования, в котором стороны равны настолько насколько это возможно. Он вслед за Тиссеном ввел понятие естественного соседа для двух наиболее близко расположенных точек наблюдения. Если провести через эти две точки окружность, то первая точка, которая попадет в этот круг и будет естественным соседом, стороны вновь образованного треугольника в этом случае будут почти равны или будут наиболее равными из всех других возможных вариантов. Однако были выдвинуты другие идеи приведения точек наблюдения к равномерному виду. Наибольшее значение получила идея приведения неравномерно расположенных точек наблюдения в равномерно расположенные точки по сети или гриду (grid) через сглаживание, а сама эта процедура получила название gridding. Одним из первых, кто предложил эту методологию, был южноафриканский геолог Дени Криге. Он обратил внимание, что содержание золота в блоке после отработки было с более низким содержанием, чем по разведочным данным и предложил проводить сглаживание скользящим окном и рассчитывать для блока скользящее среднее, что являлось лучшей оценкой истинного среднего в отрабатываемом блоке. Рекомендуется проводить трехкратное сглаживание. Сглаживание, при котором убираются пики значений признаков, еще называют фильтрацией. В технике известны фильтры более 100 разновидностей. Один из самых простых фильтров – это трехчленный фильтр Шеппарда, ранее Каллистов рекомендовал использовать пятичленный фильтр Шеппарда, в котором используются не равные коэффициенты перед значениями. Позднее Матерон – основатель геостатистики предложил геологическое сглаживание называть кригингом в честь Дени Криге.
Расчет значения средних точек грида или блоков для трехмерного случая и есть задача интерполирования. Среди многочисленных методов интерполирования наибольшее развитие получили несколько методов.
1. Полигональный метод. Если есть рассеянное множество точек, то можно представить, что каждая точка, лежащая внутри многоугольника расположена ближе к любой другой точке, содержащейся в ней, чем в точке вне его. Множества многоугольников с такими свойствами называют многоугольниками Тиссена, Дирихле, Вороного. Модель Вороного является трехмерным обобщением многоугольников (примером является совокупность мыльных пузырей). К полигональному методу близки методы - триангуляция Делоне и метод естественного соседа. При интерполяции методом естественного соседа на плане находятся две наиболее близко расположенные точки наблюдения, если провести через эти две точки окружность, то первая точка, которая попадет в этот круг и будет естественным тиссеновским соседом. Среднее значение в вновь образованном треугольнике присваивают центру совпадающей с треугольником ячейки грида или селла.
2. Метод ближайшего соседа (Nearest Neighbour – этот метод реализован в программе Datamine Studio). В трехмерных программах типа Datamine Studio значения интерполируются в центры элементарных блоков (cells) в блочных моделях. Значение в блоке рассчитывается как среднеарифметическое из окружающих точек наблюдений, находящихся в соседних блоках.(По Девису расстояние между ближайшими соседями находится по формуле пуассоновского распределения (для дискретных данных).
d=1/2√Α/n,
где А- площадь карты, n - количество точек наблюдения.
В каждой средней точке блока есть ее ближайшие соседи, которые могут быть найдены по этой формуле, точек должно быть не менее 4-6, в этом случае уже можно рассчитать среднее для данного блока.)
Здесь содержание присваивается по пробе наиболее близко расположенной к блоку.
3. Метод обратных расстояний (Inverse Power of Distance - этот метод реализован в программе Datamine Studio). Оценивание содержания в блоке методом обратных расстояний основано на формуле:
𝑥 = (𝑥1/d12+𝑥2/d22+𝑥3/d32…..):(1/d12 + 2/d22 + 3/d32…..)
Предполагается, что при интерполяции, при расчете значения в конкретном блоке будут участвовать все пробы, попадающие в эллипсоид поиска, но большее влияние при расчете будут иметь близко расположенные пробы, и наименьшее влияние будут оказывать пробы расположенные на удалении. Этот метод интерполяции сейчас самый популярный в мире и наиболее часто используется. Большое значение в этом методе имеет степень (Power), которая принимается для вычислений в каждом конкретном случае.
4. Кригинг и его разновидности (ordinary kriging- обыкновенный кригинг, simple kriging – простой кригинг – этот метод реализован в программе Datamine). При его применении необходим анализ вариограмм, так как характеристики вариограммы и используются в уравнении, рассчитывающем интерполяционные оценки блоков.
5. Метод оценки Сишела (Sichel’s T Estimator). Этот метод используется для интерполяции непараметрических массивов данных.