При рассмотрении рассеяния медленных нейтронов в веществе в условиях, далеких от резонансного захвата их атомными ядрами, обычно исходят из борновского приближения, соответствующему первому теории возмущений. Это приближение эквивалентно предположению, что падающая волна существенно не искажается рассеивающим потенциалом.
Пусть начальное состояние рассеивателя характеризуется волновой функцией 
çn), являющейся собственной функцией гамильтониана Н рассеивателя, так что
H çn) = E çn) (2.1)
При взаимодействии с нейтроном рассеиватель перейдет в другое стационарное состояние, а нейтрон может изменить свой импульс и спин. Начальное состояние нейтрона описывается волновой функцией ç k), где k – волновой вектор.
Вероятность процесса, когда нейтрон после взаимодействия с рассеивателем перейдет в состояние ç k ’), а рассеиватель в состояние çn’) – золотое правило Ферми:
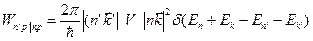(2.2)
где V – оператор взаимодействия нейтрона с рассеивателем, E n, E k, E n’, E k’ энергия нейтрона и рассеивателя до момента рассеивания и после него.
Полная вероятность процесса рассеяния получается суммированием вероятностей W n’k’çnk по конечным состояниям рассеивателя и усреднением по начальным состояниям:
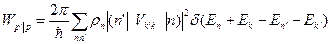(2.3)
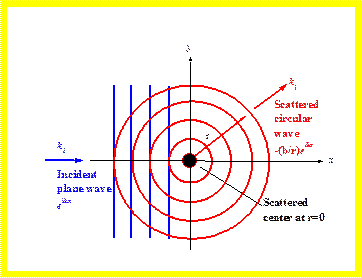
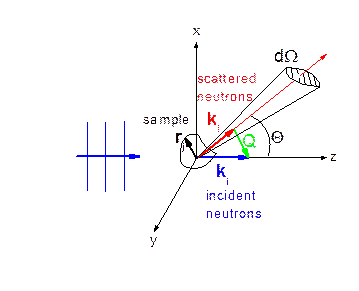
Схема, иллюстрирующая описание рассеяния:
 |
Воспользуемся интегральным представлением для d-функции
= 
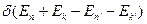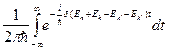(2.4)
Получаем
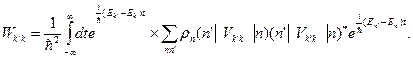(2.5)
Поскольку E n и E n’ являются собственными значениями гамильтониана Н рассеивателя, можно записать
= 
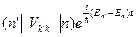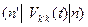(2.6)
где
= 
,
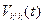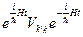есть гейзенберговское представление оператора V k’k с гамильтонианом H. Теперь выражение для W p’p запишется в виде
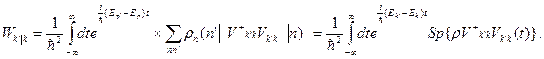
Если рассеиватель находится в равновесии при температуре Т, то
|
|
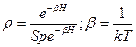
Введя символ статистического усреднения
<…….> = 
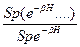
Если волновые функции нейтрона нормированы на единицу (на d-функцию), то эффективное сечение рассеяния, рассчитанное на единицу телесного угла и единичный интервал энергии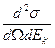 
, связано с этой вероятностью соотношением
= 
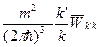(2.7)
черта сверху означает усреднение по состояниям спина нейтрона в начальном пучке и суммирование по состояниям спина в рассеянном пучке, m - масса нейтрона.
Тогда, эффективное сечение рассеяния нейтрона равно
= 
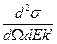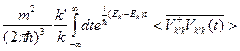(2.8)
Черта над оператором сверху означает
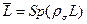, (2.9)
где r s - оператор спиновой плотности в начальном пучке.
Итак, в общем случае эффективное сечение рассеяния нейтронов в веществе прямо пропорционально Фурье-компоненте коррелятора взаимодействий. Переменная величина t имеет размерность времени.
В прошлой лекции мы использовали псевдопотенциал для описания взаимодействия нейтрона с ядром:
V (r n) = ad(r n - R), (2.10)
где r n и R – координаты нейтрона и ядра, a - определяется амплитудой рассеяния нейтронов свободным ядром.
В случае взаимодействия нейтрона с системой N ядер матричный элемент V kk’ оператора V между состояниями нейтрона с импульсом ħ k и ħ k ’запишется в виде:
V kk ’ =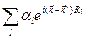 
(2.11)
Введя обозначение для вектора рассеяния q = k – k ’, окончательно получаем,
= 
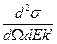(2.12)
Вектор рассеяния равен
q =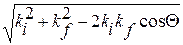 
.
В случае упругого рассеяния (E k = E k’ Û ú k ú = ú k’ ú).
Дифференциальное сечение упругого рассеяния нейтронов на ядрах можно получить из (2.12), если во втором корреляторе выделить член, не зависящий от времени:
= 
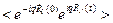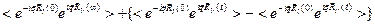
Поскольку положения атомов на бесконечно большом отрезке времени не коррелируют между собой, первый член в правой части, ответственный за упругое рассеяние, равен
|
|
= 
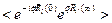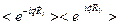(2.13)
Подставляя разложение (2.13) в (2.12) и интегрируя по энергиям рассеянных нейтронов, получим для эффективного сечения упругого рассеяния, рассчитанного на единицу телесного угла, выражение
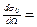
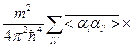
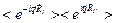(2.14)
Для простоты примем, что положения атомов зафиксированы, а амплитуды рассеяния атомов одинаковы, тогда
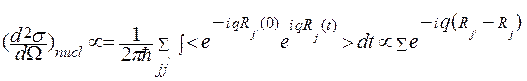. (2.15)
Решеточная сумма ограничена значениями q ×(R j¢ - R j) = 2pn, где n целое число, если q соответствует вектору обратной решетки t.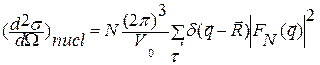 
, (2.16)
где
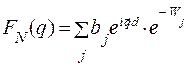. (2.17)
F N(q) – структурный фактор, d j – позиция атома в элементарной ячейке V 0 – объем элементарной ячейки.
Из (2.16) видно, что пики когерентного рассеяния возникают только при
q = t, (2.18)
что эквивалентно закону Вульфа-Брэгга.