2.2.1 В нейтрон-дифракционном эксперименте используется, в основном, два метода. В одном из них (Брегг-Брентано метод) используется геометрия отражения, а в другом (метод Лауэ) – геометрия на прохождение. Следующий рисунок показывает направления падающей и отраженной волн в геометрии отражения и прохождения.
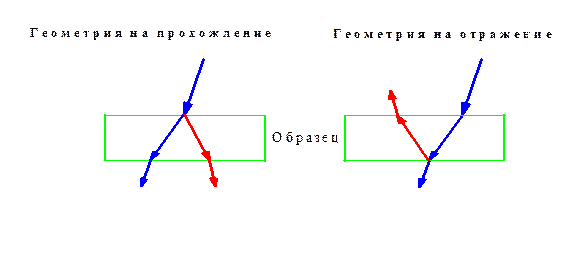
Если выполняется кинетическая теория и отсутствует поглощение, то формулы, описывающие рассеяние, примерно, одинаковы для обоих случаев. Если динамическая теория выполняется, то в случае геометрии отражения рефлексы показывают «стол Дарвина», т.е. рефлексы имеют плоские вершины.
2.2.2 Методы сканирования в нейтронном эксперименте:
a) вращающийся кристалл ® кристалл вращается вокруг вертикальной оси, детектор поворачивается с шагом D2Q.
w - сканирование ® кристалл поворачивается с шагом Dw, а детектор зафиксирован на Брегговском угле.
d) Q / Q - scanning ® кристалл и детектор поворачиваются на один и тот же угол;
e) Q / 2Q -scanning ® детектор поворачивается на угол в два раза больший, чем угол, на который поворачивается кристалл.
При выборе метода сканирования нужно иметь в виду, что сканирующий объем должен быть минимальный. Можно охарактеризовать этот объем величиной Wi :
Ww = 2 tgQ×Dl/l + a + 2P^cosQ, (2.19)
WQ/Q = tgQ×Dl/l + M + P^cosQ + P||sinQ, (2.20)
WQ/2Q = 2M + a + 2P||sinQ, (2.21)
where, Q - угол рассеяния; l and Dl - длина волны нейтронов и дисперсия по длине волны; M – угол разориентации зерен кристалла; a расходимость падающего пучка; P^ и P|| размер образца относительно отражающей плоскости. Обычно, наиболее высокое разрешение достигается при использовании метода w-сканирования, а метод Q/2Q-сканирования позволяет получать правильное соотношение между интенсивностями рефлексов.
Нейтронограмма, полученная методом, вращающегося кристалла
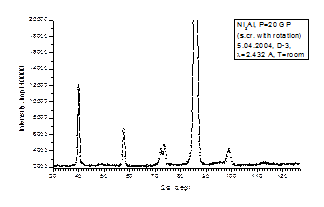
2.3 Интегральная интенсивность рефлекса
В кинематическом приближении интегральная интенсивность Брегговского рефлекса выражается следующей формулой
I (hkl) =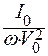 
l3× j(hkl) × F 2 (hkl) × LA(hkl) × T(hkl) × y -1/2× R(hkl) ×d V, (2.22)
где, I 0 – интенсивность падающего пучка; w скорость сканирования; l длина волны нейтронов; V 0 – объем элементарной ячейки; j(hkl) – фактор повторяемости; F(hkl) – структурный фактор; L – геометрический фактор (или фактор Лоренца); A(hkl) – коэффициент поглощения; T(hkl) – температурный фактор; y -1/2 – поправка на экстинцию; R(hkl) – поправка на преимущественную ориентацию; d V – объем сканирования образца.
Фактор повторяемости
Если кристаллографические плоскости характеризуются одним и тем же межплоскостным расстоянием, то эти плоскости дают вклад в интенсивность одного и того же рефлекса (в случае поликристаллического образца). Значение фактора повторяемости равно числу плоскостей, имеющих одинаковые межплоскостные расстояния.
Например, в случае образца с кубической структурой фактор повторяемости можно рассчитать с помощью перестановок hkl - индексов. Пусть рассматриваемая плоскость есть (111), тогда получаем все перестановки (111), (-1-1-1), (1-1-1), (-111), (1-11), (-11-1), (11-1), (-1-11), их число равно 8; следовательно, j(111) = 8.
В случае гексагональной структуры удобно использовать четырехзначную систему индексов. В ней четвертый индекс вводится как: (hkl) ® (hkil), i = - (h + k). Например, пусть (hkl) это (111), тогда в четырехиндексовой системе это есть (11-21), используя перестановки получаем (11-21), (-2111), (1-211), (-1-121), (-12-11), (2-1-11), (11-2-1),
(-211-1), (1-21-1), (-1-12-1), (-12-1-1), (2-1-1-1); следовательно, j(111) = 12.
2.3.3 Структурный фактор
Структурный фактор выражается следующим соотношением
F ( hkl ) =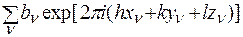 
, (2.23)
где, xn, yn, zn - координаты атома. При расчетах используются следующие выражения:
F 2( hkl ) = A 2( hkl ) + B 2( hkl ),
A ( hkl ) =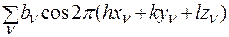 
,
B (hkl) =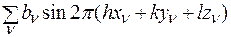 
, (2.24)
tgj(hkl) = B(hkl) / A(hkl),
где, j (hkl) – фаза рефлекса hkl.
Фактор интегральности (или фактор Лоренца)
При пересчете интегральных интенсивностей отражений в структурные факторы следует учитывать специфику различных методов сканирования. Формально это сделано введением множителя Lhkl. Каждый узел, попадающий в отражающее положение, дает дифрагированный пучок до тех пор, пока хотя бы частично находится на реальной сфере Эвальда. Фактор интегральности учитывает разное время прохождения узлом обратной решетки сферы отражения. Так как в процессе съемки расстояние отражающего узла обратной решетки до оси вращения кристалла изменяется, то возникает дополнительная угловая зависимость дифрагированного луча. В общем случае фактор интегральности можно рассчитать по формуле:
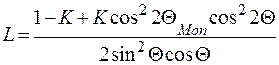(2.25)
где, K= 0.0 для нейтронов. Для плоского образца, размещенного в симметричной позиции (на прохождение), полностью перекрывающего нейтронный пучок, фактор L равен:
L = 1/sin22Q. (2.26)
Для поликристаллического образца в форме вертикального кругого цилиндра, «купающегося» в нейтронном пучке L равно:
L = 1/sinQsin2Q. (2.27)
Для монокристалла L равно:
L = 1/sin2Q. (2.28)
Коэффициент поглощения
Уменьшение интенсивности падающего на кристалл пучка нейтронов по мере проникновения на глубину t описывается
I = I 0exp(- mt), (2.29)
где, m линейный коэффициент поглощения.
Для плоского образца, размещенного в симметричной позиции (на прохождение), полностью перекрывающего падающий пучок коэффициент поглощения равен:
A(hkl) = exp(- mt× secQ hkl), (2.30)
где, t – толщина пластинки. На практике значение mt определяют прямым измерением уменьшения интенсивности пучка в нулевой позиции, как отношение двух интенсивностей - exp(- mt).
В случае цилиндрического образца, который купается в нейтронном пучке, коэффициент поглощения может быть найден в литературе для широкого интервала значения mR s (где R s – радиус цилиндрического образца). Например, можно использовать таблицу в книге Бэкона «Нейтронная дифракция», Таблица 10 на странице 113, издание (1975 г.).
Температурный фактор
Ядро атома имеет размер ~ 10-15 м. Тепловое движение размазывает его по некоторой области, объем которой по порядку величины совпадает с размером атома. Рассеяние нейтронов на колеблющихся атомах можно интерпретировать как результат интерференции нейтронных волн, рассеянных в данном направлении различными участками «теплового облака» ядерной плотности. Этот процесс описывается температурным фактором Дебая – Уоллера.
Температурный фактор можно выразить как
T = exp(-2 B) (2.31)
В гармоническом приближении B равно
B n = 8p(sinQ/l)2 Ū 2n, (2.32)
где, Ū 2n - средне квадратичное отклонение смещения n-атома от положения равновесия.
Преимущественная ориентация
В качестве одного из способов учета преимущественной ориентации можно использовать следующее выражение (см. Руководство по программе Fullprof):
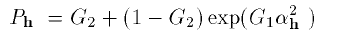, (2.33)
где, G 1 и G 2 уточняемые параметры ah – угол между вектором рассеяния и перпендикуляром к кристаллитам.