Малое предприятие выпускает два вида деталей. На их изготовление идет три вида ресурсов R 1, R 2, R 3, выделяемых предприятию в ограниченных количествах.
Данные о наличии и расходе материалов, себестоимость 1 000 шт. деталей каждого вида, а также оптовая цена за 1 000 шт. приведены в табл. 44.
Составить план выпуска деталей, обеспечивающий получение максимальной прибыли.
Решение задачи включает этапы, описанные в пп 3.2.2.-3.2.4.
Таблица 44
| Виды материалов | Запасы (усл. ед.) | Расход материалов на 1000 ед. деталей (усл. ед) | |
| Деталь А | Деталь В | ||
| R 1 | |||
| R 2 | |||
| R 3 | |||
| Себестоимость 1000 шт. (усл. ед.) | 3,8 | 3,5 | |
| Оптовая цена 1000 шт. (усл. ед.) |
Построение математической модели
Обозначим:
Х 1 – число выпускаемых деталей А (в тысячах штук);
Х 2 – число выпускаемых деталей В (в тысячах штук).
На неизвестные величины накладываются два вида ограничений:
Первое. По физическому смыслу (число деталей неотрицательно)
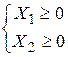 (13)
(13)
Второе. По запасам ресурсов:
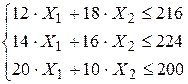 (14)
(14)
Для расчета целевой функции (прибыли от продажи выпускаемых деталей) рассчитаем прибыль, получаемую от тысячи деталей каждого вида.
Для деталей А: 5 - 3,8 = 1,2.
Для деталей В: 6 - 3,5 = 2,5.
Тогда целевая функция равна
Z = 1,2 X 1 + 2,5 X 2 (15)
Требуется найти такие значения неизвестных Х 1 и Х 2, которые обеспечивают максимум целевой функции (13) при выполнении ограничений (14) и (15).
3.2.5.2. Построение начального плана решения
План решения аналогичен описанному в п. 3.2.4 и приведен в табл. 45 и табл. 46.
Таблица 45
| A | B | C | D | E | F | |||
| Задача распределения ресурсов | ||||||||
| План выпуска | Целевая функция | |||||||
| Деталь А | Деталь В | Доход от 1000 деталей А | Доход от 1000 деталей В | Значение целевой функции | ||||
| 1,2 | 2,5 | 3,7 | ||||||
| Ограничения | ||||||||
| Расход материала на 1000 деталей | Левая часть системы (14) | Правая часть системы (14) | ||||||
| Для R1 | ||||||||
| Для R2 | ||||||||
| Для R3 | ||||||||
3.2.5.3. Оптимизация плана решения
Основы оптимизации, описаны в п. 3.2.4. Диалоговое окно Поиск решения приведено на рис. 13 – а оптимальный план решения – в табл. 47.
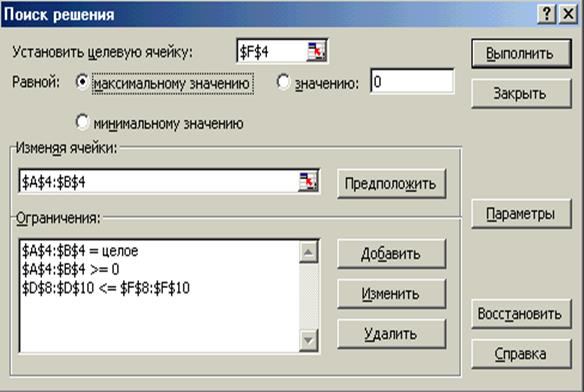
Excel Microsoft Office

OpenOffice.org Calc
Рис. 13
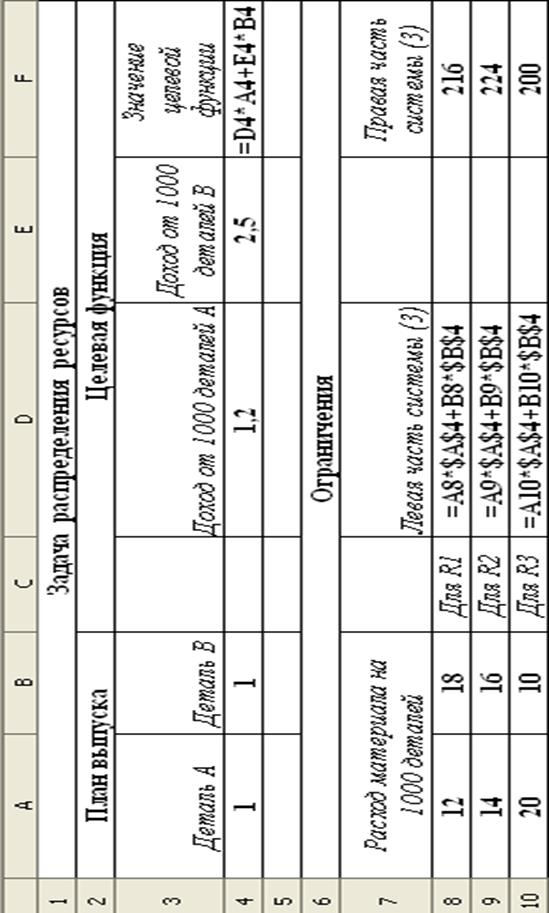
Таблица 47
| A | B | C | D | E | F | |
| Задача распределения ресурсов | ||||||
| План выпуска | Целевая функция | |||||
| Деталь А | Деталь В | Доход от 1000 деталей А | Доход от 1000 деталей В | Значение целевой функции | ||
| 1,2 | 2,5 | |||||
| Ограничения | ||||||
| Расход материала на 1000 деталей | Левая часть системы (14) | Правая часть системы (14) | ||||
| Для R1 | ||||||
| Для R2 | ||||||
| Для R3 |
Задача об оптимальном составе сплава
Для получения сплавов А и В используются четыре металла I, II, III и IV. Характеристики и запасы руд, из которых получают эти металлы, указаны в табл. 48.
Требования к содержанию металлов I, II, III и IV в сплавах, а также стоимости одной тонны сплавов при продаже приведены в табл. 49.
Необходимо максимизировать прибыль от продажи сплавов А и В.
Таблица 48
| Руда | Максимальный запас, тонны | Состав, % | Цена, доллары за тонну | ||||
| I | II | III | IV | Другие компоненты | |||
Таблица 49
| Сплав | Требование к содержанию металла | Цена одной тонны сплава, в долларах |
| А | Не более 80% металла I | |
| Не более 30% металла II | ||
| В | От 40% до 60% металла II | |
| Не менее 30% металла II | ||
| Не более 70% металла IV |
Решение включает этапы, описанные в пп. 3.2.2 -3.2.5.