ОСНОВЫЦИФРОВОЙ ТЕХНИКИ
Методические указания к выполнению лабораторных работ
Братск
Издательство Братского государственного университета
УДК 004.3
Ульянов А.Д. Основы цифровой техники: методические указания/ А.Д. Ульянов, Е.В. Прусенкова.- Братск: Изд-во БрГУ, 2017.-66 с.
Методическое указание содержит лабораторные работы по дисциплине «Информатика», включающие основные понятия о представлении чисел в различных системах счисления и выполнении арифметических действий с кодированными числами, основные понятия алгебры логики; и т.д. По теме каждой работы широко представлены примеры выполнения заданий.
Предназначено для студентов по направлению 11.03.02 «Инфокоммуникационные технологии и системы связи» очной формы обучения.
Рецензент И. В. Игнатьев, канд. тех. наук, профессор, зав. кафедрой «Управление в технических системах» (ФГБОУ ВО «БрГУ» г. Братск).
Отпечатано с оригинала автора
в издательстве ФГБОУ ВО «БрГУ»
665709, Братск, ул. Макаренко, 40
Тираж 50 экз. Заказ
© ФГБОУ ВО «БрГУ», 2017
© Ульянов А.Д., Прусенкова Е.В. 2017
ОГЛАВЛЕНИЕ
Введение 4
Лабораторная работа №1 Арифметические основы цифровой
техники 6
Лабораторная работа №2 Кодирование чисел 20
Лабораторная работа №3 Логические основы цифровой
техники 36
ВВЕДЕНИЕ
Информатика – комплекс научно-практических дисциплин, изучающих все аспекты получения, хранения, преобразования, передачи и использования информации. У современной информатики есть два взаимодополняющих аспекта - научный и технологический. Первый является наиболее устоявшимся, второй – весьма мобильным, хотя и в технологической части информатики есть вполне сформировавшиеся ядро, которое мало подвержено изменениям.
Итак, главное при изучении информатики – освоить фундаментальные понятия каждой из ее областей, научиться ориентироваться в их взаимосвязи; приобрести навыки практической работы с важнейшими техническими и программными средствами.
Лабораторные работы по курсу «Информатика», представленные в настоящем пособии, позволят студентам освоить методы обработки информации в микропроцессорных системах (МПС), синтеза систем управления и программирования, а также изучать принципы работы элементов и устройств МПС. В данном методическом пособие представлены лабораторные работы изучаемые студентами в первом семестре дисциплины Информатика.
Большое количество примеров выполнения заданий, приведенных в каждой теме, поможет им закрепить теоретические знания о представлении чисел в различных системах счисления, о выполнении арифметических действий с кодированными числами, о минимизации булевых функций.
После изучения данного курса, студент должен овладеть основными методами, способами и средствами получения, хранения, переработки информации. А также:
• Понимать сущность и значение информации в развитии современного информационного общества, осознавать опасности и угрозы, возникающие в этом процессе, соблюдать основные требования информационной безопасности, в том числе защиты государственной;
• Иметь навыки самостоятельной работы на компьютере и в компьютерных сетях, осуществлять компьютерное моделирование устройств, систем и процессов с использованием универсальных пакетов прикладных компьютерных программ;
• Должен быть готов к изучению научно-технической информации, отечественного и зарубежного опыта по тематике проекта.
Лабораторная работа №1
АРИФМЕТИЧЕСКИЕ ОСНОВЫЦИФРОВОЙ ТЕХНИКИ
Цель работы: изучить позиционные системы счисления; получить практические навыки по переводу чисел из одной системы счисления в другую и по выполнению арифметических действий над двоичными числами;
Основные теоретические сведения
1.1 Система счисления (с/с) – это совокупность приемов и правил представления чисел посредством ограниченного набора символов. Множество символов, используемых для записи чисел, называют цифрами.
Непозиционная с/с – система, в которой количественный эквивалент цифры не зависит от места ее расположения в записи числа. Примером непозиционной с/с является римская система счисления, в которой используются принципы сложения и вычитания. Например, запись XV соответствует числу 15 (X - десять, V - пять), а запись IX – числу девять. Непозиционные с/с характеризуются очень сложными и громоздкими алгоритмами представления чисел и выполнения арифметических действий и в цифровой вычислительной технике не применяются.
Позиционная с/с – система, в которой количественный эквивалент цифры зависит от ее местоположения в записи числа. Например, в записи 545 цифра 5 встречается дважды, однако ее количественный эквивалент в обоих случаях различен: крайняя правая цифра 5 обозначает число единиц – пять, а левая цифра 5 обозначает число сотен – пятьсот.
Главным преимуществом позиционных систем счисления по сравнению с непозиционными является удобство представления чисел и простота выполнения арифметических действий.
Основание позиционной с/с – количество цифр, используемых для записи чисел. Основания для наиболее употребительных позиционных с/с приведены в табл. 1.1.
Таблица 1.1
Позиционные системы счисления
| Основание | Система счисления | Символы |
| Двоичная | 0,1 | |
| Восьмеричная | 0,1,2,3,4,5,6,7 | |
| Десятичная | 0,1,2,3,4,5,6,7,8,9 | |
| Шестнадцатеричная | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F |
При написании числа систему счисления обозначают индексом, проставленным справа внизу у числа и представляющим собой основание соответствующей с/с, записанное в десятичной системе. Так, записи некоторых чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления выглядят следующим образом:
11011,01₂; 431,67₈; А28Е, С4₁₆.
В позиционных системах счисления используют принцип умножения и сложения. В таких системах с основанием q произвольное число
N= 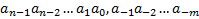
записываются в общем виде:

 (1.1)
(1.1)
или
 ,
,
где q – основание системы счисления;  – цифры, лежащие в диапазоне
– цифры, лежащие в диапазоне  ; m – число разрядов справа от запятой (дробная часть числа); n – число разрядов слева от запятой (целая часть числа).
; m – число разрядов справа от запятой (дробная часть числа); n – число разрядов слева от запятой (целая часть числа).
Пример 1.1.
789,35₁₀; 1101,0101₂; D3F,4₁₆; 657,341₈.
N=789,35₁₀=7·10²+8·10¹+9¹·10⁰+3·10⁻¹+5·10⁻²;
N=1101,0101₂=1·2³+1·2²+0·2¹+1·2⁰+0·2⁻¹+1·2⁻²+0·2⁻³+1·2⁻⁴;
N=D3F,4₁₆=D·16²+3·16¹+F·16⁰+4·16⁻¹;
N=657,341₈=6·8²+5·8¹+7·8⁰+3·8⁻¹+4·8⁻²+1·8⁻³
1.2 Преобразование чисел из одной системы счисления в другую – это эквивалентные представления одной и той же величины в разных системах счисления.
Для преобразования числа из недесятичной позиционной системы счисления в десятичную форму необходимо записать число в виде многочлена (1.1) и произвести его вычисление, пользуясь десятичной арифметикой. При этом для системы счисления, где цифры представлены буквами, последние при вычислении заменяют на десятичные эквиваленты, например: A=10, B=11, C=12, D=13, E=14, F=15.
Пример 1.2. Перевести в десятичную систему счисления числа 1011,101₂; 2AE₁₆.
1011,101₂=1·2³+0·2²+1·2¹+1·2⁰+1·2⁻¹+0·2⁻²+1·2⁻³=11,625₁₀;
2 АЕ₁₆=2·16²+А·16¹+Е·16⁰=2·16²+10·16¹+14·16⁰=686₁₀.
Для преобразования десятичного числа в эквивалентную форму в другой системе счисления необходимо отдельно переводить целую и дробную части числа.
Для перевода целого десятичного числа в другую систему счисления его нужно последовательно делить на основание той системы счисления, в которую оно переводится. При этом деление ведут до тех пор, пока частное (остаток от деления) не будет меньше основания, на которое число делят.
Число в новой системе счисления записывают в виде последнего частного и всех остатков деления, начиная с последнего. Последний остаток (частное) дает старший разряд (цифру) числа.
Пример 1.3. Перевести из десятичной системы счисления в восьмеричную число 191₁₀.

Итак: 191₁₀ = 277₈.
Пример 1.4. Перевести из десятичной системы счисления в двоичную число 100₁₀

Итак: 100₁₀ = 1100100₂.
Пример 1.5. Перевести из десятичной системы счисления в шестнадцатеричную число 6703₁₀.
Так как 15 = F, 10 = A, то получаем 6703₁₀=1А2F₁₆.
Для перевода дробной части десятичного числа (или правильной дроби) в другую систему счисления ее необходимо последовательно умножать на основание той системы, в которую она переводится. При этом перемножают только дробные части числа. Дробную часть десятичного числа (или правильной дроби) в новой системе записывают в виде целых частей получаемых произведений, начиная с первого сомножителя.
Пример 1.6. Перевести из десятичной системы счисления в двоичную систему дробь 0,3125₁₀.

Итак: 0,3125₁₀ = 0,0101₂.
Пример 1.7. Перевести из десятичной системы счисления в восьмеричную систему дробь 0,6875₁₀.

Итак: 0,6875₁₀ = 0,54₈.
Пример 1.8. Перевести из десятичной системы счисления в шестнадцатеричную систему дробь 0,8435₁₀.

Остановив процесс в этом месте и приняв во внимание, что 13 = D;
14 = E; 15 = F в шестнадцатеричной системе счисления, получим
0,8435₁₀ = 0,D7EF…₁₆.
Представление первых 20 чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления и их десятичных эквивалентов дано в табл. 1.2.
Таблица 1.2.
Запись первых 20 чисел в системах счисления
| Десятичные | Двоичные | Восьмеричные | Шестнадцатеричные |
| 0 | 000 | 0 | 0 |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
1.3. Двоично-восьмеричные и двоично-шестнадцатеричные преобразования. Для преобразования двоичного числа в восьмеричную форму необходимо объединить двоичные цифры в группы по 3 разряда, продвигаясь от разделительной точки (запятой) вправо и влево. При необходимости в начале и в конце исходного числа добавляются нули. Затем каждую группу из трех разрядов заменяют эквивалентной восьмеричной цифрой. Результат будет восьмеричным представлением исходного двоичного числа.
Пример 1.9. Преобразовать двоичное число 11011001,1011₂ в восьмеричную форму.
11011001,1011₂ = 011 011 001, 101 100₂ = 331,54₈.
³ ³ ¹ ⁵ ⁴
Для преобразования восьмеричного числа в двоичную форму необходимо каждую цифру заменить трехразрядным двоичным числом. При этом незначащие нули отбрасываются.
Пример 1.10. Преобразовать восьмеричное число 305,4₈ в двоичную форму.
305,4₈ = 011 000 101, 100₂ = 11000101,1₂.
³ ⁰ ⁵ ⁴
Для преобразования двоичного числа в шестнадцатеричную форму необходимо объединить двоичные цифры в группы по 4 разряда, продвигаясь от разделительной точки (запятой) вправо и влево. При необходимости в начале и в конце исходного числа добавляют нули. Затем каждую группу из четырех разрядов заменяют эквивалентной шестнадцатеричной цифрой. Результат будет шестнадцатеричным представлением исходного двоичного числа.
Пример 1.11. Преобразовать двоичное число 1010111,1101101₂ в шестнадцатеричную форму.
1010111,1101101₂= 0101 0111, 1101 1010₂ = 57,DA₁₆.
⁵ ⁷ ᴰ ᴬ
Для преобразования шестнадцатеричного числа в двоичную форму необходимо каждую цифру заменить четырехразрядным двоичным числом. При этом незначащие нули отбрасываются.
Пример 1.12. Преобразовать шестнадцатеричное число 2Е5,С₁₆ в двоичную форму:
2Е5,С₁₆= 0010 1110 0101, 1100₂ = 1011100101,11₂.
² ᴱ ⁵ ᶜ
1.4. Двоичная арифметика
Правила сложения двоичных чисел:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Правила вычитания двоичных чисел:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
10 - 1 = 1
Правила умножения двоичных чисел:
0 · 0 = 0
0 · 1 = 0
1 · 1 = 0
1 · 1 = 1
Для сложения двух двоичных чисел необходимо применить правило сложения многократно, отправляясь от пары младших (крайних правых) разрядов, как это делается при десятичном сложении. После сложения пары младших цифр и получения значения младшего разряда суммы складывают следующую пару цифр с учетом переноса из младшего разряда.

Двоичное вычитание обратно двоичному сложению. При вычитании большей цифры из меньшей необходимо произвести «заём» в более старшей соседней позиции. Так, если в позиции n возникает необходимость «заема», то вычитают 1 из (n+1)-й цифры уменьшаемого, а в позицию n «приносят» величину 2, т.е. основание системы счисления.

Умножение двух многоразрядных двоичных чисел проводят аналогично умножению десятичных чисел, т.е. сначала вычисляют
частные произведения множимого на отдельные разряды множителя, а затем эти частные произведения суммируют.

Двоичное деление также аналогично делению десятичному, т.е. последовательно подбирают очередную искомую цифру частного и на нее умножают делитель, а полученное произведение вычитают из делимого для проверки правильности подобранной цифры.

Варианты индивидуальных заданий
1. Перевести в десятичную систему счисления следующие числа (табл. 1.3)
Таблица 1.3.
| Вариант | Двоичное число | Восьмеричное число | Шестнадцатеричное число |
| 101100,1001 | 564,21 | FC,8B | |
| 11000,0011 | 477,26 | A4,46 | |
| 101101,101 | 264,74 | 78,FF | |
| 100011,1001 | 236,14 | 87,DA | |
| 101011,1101 | 761,37 | 46,EA | |
| 111101,101 | 214,67 | 99,01 | |
| 1100011,111 | 136,45 | DA,47 | |
| 1001001,1011 | 176,47 | 65,F7 | |
| 110111,11101 | 665,13 | 91,52 | |
| 1101010,11 | 117,36 | 92,76 | |
| 111011,11001 | 772,16 | 11,FF | |
| 1111000,0001 | 423,36 | 56,35 | |
| 10001100,001 | 331,44 | 98,A5 | |
| 1100100,0011 | 127,33 | 95,CB | |
| 1100100,1101 | 113,64 | 62,F9 | |
| 10000011,111 | 331,24 | 13,E6 | |
| 110011,11011 | 164,66 | EB,6A | |
| 1111,1000001 | 124,63 | BC,FC | |
| 110110,11001 | 123,17 | FF,01 | |
| 1111000,1101 | 745,31 | F9,25 | |
| 1000111,001 | 217,36 | 31,CD | |
| 111,0000011 | 254,74 | 38,CF | |
| 1111,1111101 | 654,12 | 87,13 | |
| 111100,0111 | 147,64 | 99,AA |
2. Осуществить перевод десятичного числа в другие СС (табл. 1.4)
Таблица 1.4.
| Вариант | Десятичное число | Перевести в систему счисления | ||
| В N2 | В N8 | В N16 | ||
| 85.14 | + | + | ||
| 246.4 | + | + | ||
| 13.24 | + | + | ||
| 58.11 | + | + | ||
| 2.675 | + | + | ||
| 21.64 | + | + | ||
| 98.44 | + | + | ||
| 123.5 | + | + | ||
| 143.5 | + | + | ||
| 14.26 | + | + | ||
| 31.26 | + | + | ||
| 147.1 | + | + | ||
| 9.165 | + | + | ||
| 132.2 | + | + | ||
| 14.59 | + | + | ||
| 45.31 | + | + | ||
| 247.6 | + | + | ||
| 25.47 | + | + | ||
| 789.1 | + | + | ||
| 32.47 | + | + | ||
| 99.54 | + | + | ||
| 16.58 | + | + | ||
| 798.1 | + | + | ||
| 8.369 | + | + |
3. Преобразование числа в соответствующие системы счисления (табл. 1.5):
· Двоичное число преобразовать в восьмеричную и шестнадцатеричную СС,
· Восьмеричное число преобразовать в двоичную СС,
· Шестнадцатеричное число преобразовать в двоичную СС.
Таблица 1.5
| Вариант | Двоичное число | Восьмеричное число | Шестнадцатеричное число |
| 101100,1001 | 544,21 | FC,9B | |
| 11000,0011 | 427,26 | A5,46 | |
| 101101,101 | 264,84 | 98,FF | |
| 100011,1001 | 736,14 | 97,DA | |
| 101011,1101 | 721,37 | 45,EA | |
| 111101,101 | 214,37 | 96,01 | |
| 1100011,111 | 146,45 | 4A,57 | |
| 100100,1011 | 174,47 | 62,F6 | |
| 11011,11101 | 662,13 | 21,52 | |
| 1101010,11 | 417,36 | 92,36 | |
| 111011,1001 | 772,36 | 11,5F | |
| 111000,0001 | 453,36 | 51,35 | |
| 1000110,001 | 331,64 | 38,A5 | |
| 110100,0011 | 157,33 | 95,C1 | |
| 110010,1101 | 413,64 | 42,F9 | |
| 1000011,111 | 331,64 | 13,76 | |
| 110011,1111 | 174,66 | 3B,6A | |
| 111,1000001 | 124,73 | BC,F5 | |
| 110110,1001 | 153,17 | 6F,01 | |
| 111000,1101 | 745,36 | F9,45 | |
| 1000101,001 | 257,36 | 31,9D | |
| 111,0000011 | 254,76 | 98,CF | |
| 1111,111101 | 644,12 | 67,13 | |
| 111100,0111 | 147,66 | 99,A7 |
3. Произвести сложение и вычитания двоичных чисел (табл. 1.6):
Таблица 1.6
| Вариант | Двоичные числа |
| 101100,1001 и 111011,11001 | |
| 11000,0011 и 10001100,001 | |
| 101101,101 и 1100100,1101 | |
| 100011,1001 и110011,11011 | |
| 101011,1101 и110110,11001 | |
| 111101,101 и 1000111,001 | |
| 1100011,111 и 1000111,001 | |
| 1001001,1011 и 111011,11001 | |
| 110111,11101 и 1101010,11 | |
| 1101010,11 и 101011,1101 | |
| 111011,11001 и 1000111,001 | |
| 1111000,0001 и 1111000,1101 | |
| 10001100,001 и 100011,1001 | |
| 1100100,0011 и 1111000,0001 | |
| 1100100,1101 и 1000111,001 | |
| 10000011,111 и 111011,11001 | |
| 110011,11011 и 111101,101 | |
| 1111,1000001 и 10000011,111 | |
| 110110,11001 и 110011,11011 | |
| 1111000,1101 и 100011,1001 | |
| 1000111,001 и 101011,1101 | |
| 111,0000011 и 101011,1101 | |
| 1111,1111101 и 111101,101 | |
| 111100,0111 и 101011,1101 |