3.1. Логика - это наука о законах человеческого мышления.
Математическая логика – это наука, изучающая вопросы применения математических методов для решения различных логических задач.
Алгебра логики – это начальный раздел математической логики, показывающий, как оперировать с логическими суждениями, складывать их, умножать и т.д.
Объектом исследования в алгебре логики является высказывание, т.е. любое утверждения, о котором можно сказать, что оно истинно или ложно. Содержанию высказывания не придаётся значения, каждое высказывание рассматривается лишь с точки зрения истинности. Так, если высказывание истинно, то значение его истинности принимается равным единице (1), а если же оно ложно, то значение истинности считается равным нулю (0).
Пример 3.1 Имеются высказывания:
1. Обработка данных – одна из главных функций микропроцессора.
2. Микропроцессор – это интегральная микросхема, предназначенная для обработки данных и управления.
3. Перемещение данных является функцией АЛУ микропроцессора.
Определить значение их истинности.
Первое и второе высказывания являются истинными, следовательно, значения истинности этих высказываний равно единице. Третье высказывание является ложным, следовательно, значение его истинности равно нулю.
В алгебре логики, называемой еще булевой алгеброй, 0 и 1 называются константами. Чтобы не смешивать их с двоичными цифрами, эти символы называют «логический 0» и «логическая 1».
Логические переменные – это высказывания, которые могут принимать одно из двух значений истинности: «логический 0» или «логическая 1». Для обозначения логических переменных используются латинские буквы: А, В, … Х, У….
Из простых высказываний составляются более сложные, которые также могут иметь одно из двух значений истинности: «логический 0» или «логическая 1». Это зависит от значений истинности составляющих высказываний и виды логической связи между ними.
Пример 3.2. Имеются два простых высказывания (А и В):
А: вычисление – одна из функций микропроцессора по обработке данных.
В: манипулирование данными – другая функция микропроцессора по обработке данных.
Определить значение истинности высказывания F, составленного из простых высказываний А и В.
Составляем сложное высказывание F: вычисление и манипулирование данными – функции микропроцессора по обработке данных.
Определяем значение истинности высказываний: простые высказывания являются истинными, следовательно, значения истинности этих высказываний равны единице, т.е. А = 1, В = 1; сложное высказывание также является истинным, следовательно, значение его истинности равно единице, т.е. F = 1.
Сложное высказывание, полученное в примере путем соответствующего преобразования (путем объединения союзом И), можно рассматривать как выходную переменную, а составляющие его простые высказывания – как входные переменные.
Аналогично в качестве преобразователя можно рассматривать АЛУ микропроцессора, выполняющее арифметические действия над двоичными числами, где входными переменными являются исходные двоичные числа, а выходной переменной – новое двоичное число, которое образовалось в результате выполнения данной операции. При этом как входные переменные, так и выходная переменная могут принимать лишь одно из двух возможных значений, т.е. 0 или 1.
В общем случае входных переменных может быть несколько (А₁, А₂, … 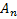 ).
).
Булевая переменная – это символ, относительно которого можно записать:
х=0, если х≠1;
х=1, если х≠0;
основными логическими операциям булевой алгебры являются:
а) логическое умножение (логическое И);
б) логическое сложение (логического ИЛИ);
в) логическое отрицание (логическое НЕ).
Операция логического И, называемая также конъюнкцией, для двух переменных математически выражается следующим образом:
F = X · Y
и читается так: F равно Х и Y, т.е. F истинно при истинно Х и Y.
Определение операции И приведено в табл. 2.2, из которой видно, что F принимает значение логической единицы тогда и только тогда, когда Х и У равны логической единице, в противном случае F равно логическому нулю.
Операция логическое ИЛИ, называется также дизъюнкцией, для двух переменных математически выражается следующим образом:
F = X + Y
и читается так: F равно X и Y, т.е. F истинно при истинно X или Y.
Определение операции ИЛИ приведено в табл. 2.2, из которой видно, что F принимает значение логического нуля тогда и только тогда, когда переменные X и Y имеют значения логического нуля, в противном случае F равно логической единице.
Операция логического НЕ, называется также инверсией, математически выражается следующим образом:
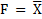
И читается так: F не есть X, т.е. F истинно при X ложно и наоборот.
Определение операции НЕ приведено в табл. 2.3, из которой следует:
F = 1, если x = 0
F = 0, если x = 1
или, что то же самое: 0 = 1, 1 = 0.
Таблица 3.1 Таблица 3.2 Таблица 3.3
| X ∙ Y | F = X·Y | X + Y | F = X+Y | X | 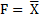
| ||
| 0 ∙ 0 | 0 + 0 | ||||||
| 0 ∙ 1 | 0 + 1 | ||||||
| 1 ∙ 0 | 1 + 0 | ||||||
| 1 ∙ 1 | 1 + 1 |
3.2 Таблица истинности (или комбинационная таблица) – это таблица, содержащая все возможные комбинации значений входных переменных вместе с соответствующими им значениями выходных переменных.
Например, при m входных и одной входной переменной таблица истинности будет содержать 2m строк:
| Х1 | Х2 | Х3 | Хm-1 | Xm | ƒ | |
| …….. | (0,0,0,…,0,0) | |||||
| …….. | (0,0,0,…,0,1) | |||||
| …….. | (0,0,0,…,1,0) | |||||
| …….. | (0,0,0,…,1,1) | |||||
| . | . | . | …….. | . | . | . |
| . | . | . | …….. | . | . | . |
| . | . | . | …….. | . | . | . |
| …….. | (1,1,1,…,1,1) |
Так, при m = 3 таблица истинности будет иметь следующий вид (число строк равно 23 = 8):
| Х1 | Х2 | Х3 | ƒ(х1,х2,х3) |
Булево выражение (булева функция) – это формула, состоящая из булевых констант и переменных, связанных операциями И, ИЛИ, НЕ.
Например: 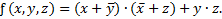
3.3. Построение таблицы истинности по булевой функции – это нахождение для каждой комбинации значений входных переменных значения функции.
Для упрощения процесса построения таблицы истинности осуществляют последовательное построение функции путем определения ее промежуточных функций.
Пример 3.3. Построить таблицу истинности по булевой функции
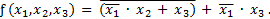
Так как m = 3, то число строк в таблице истинности составит 23 = 8.
Введем промежуточные функции:
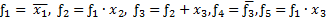 .
.
Обозначив ƒ = ƒ(х1, х2, х3), с учетом введенных промежуточных функций получим
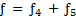 .
.
Последовательное построение таблицы истинности для функций ƒ1, ƒ2, ƒ3, ƒ4, ƒ5, ƒ имеет следующий вид:
| Х1 | Х2 | Х3 | ƒ 1 | ƒ 2 | ƒ 3 | ƒ 4 | ƒ 5 | ƒ |
Последняя колонка таблицы истинности содержит окончательные результаты всех восьми вычислений.
3.4. Минтерм – это конъюнкция (И) конечного множества булевых переменных и их отрицаний, например 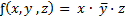 . Минтерм принимает единичное значение при одном из всех возможных наборов входных переменны, например, при х = 1; у = 0; z = 1 для минтерма ƒ(x, y, z) = x ∙
. Минтерм принимает единичное значение при одном из всех возможных наборов входных переменны, например, при х = 1; у = 0; z = 1 для минтерма ƒ(x, y, z) = x ∙ 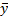 · z.
· z.
Макстерм – это дизъюнкция (ИЛИ) конечного множества булевых переменных и их отрицаний, например Р(x, y, z) = 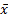 + y +
+ y + 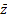 . Макстерм принимает нулевое значение при одном из всех возможных наборов входных переменных, например, при х = 1; у = 0; z = 1 для макстерма
. Макстерм принимает нулевое значение при одном из всех возможных наборов входных переменных, например, при х = 1; у = 0; z = 1 для макстерма 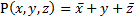 , и единичное – при всех других.
, и единичное – при всех других.
Число минтермов или макстермов совпадает с числом наборов входных переменных, т.е. для n входных переменных их будет 2n .
Нормальная форма представления булевой функции – это выражение булевой функции через инверсию, конъюнкцию и дизъюнкцию.
Конъюнктивная нормальная форма (КНФ) представления булевой функции – это логическое произведение макстермов,
например 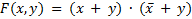
Дизъюнктивная нормальная форма (ДНФ) представления булевой функции – это логическая сумма минтермов,
например 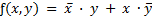 .
.
Ранг минтерма (макстерма) – это число входных переменных, образующий минтерм (макстерм). Например, функция 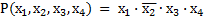 является минтермом четвертого ранга, а функция F(
является минтермом четвертого ранга, а функция F(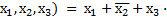 – макстермом третьего ранга.
– макстермом третьего ранга.
Дизъюнктивная совершенная нормальная форма (ДСНФ) представления булевой функции – это выражение булевой функции через минтермы одного ранга, связанные дизъюнкцией. ДСНФ еще называют канонической суммой минтермов или стандартной суммой произведений.
Например, 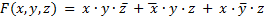 .
.
Требования, предъявляемые к ДСНФ:
- в ней не должно быть двух одинаковых конъюнкций;
- ни одна конъюнкция не должна содержать двух одинаковых переменных;
- никакая конъюнкция не должна содержать переменную вместе с ее отрицанием;
- все конъюнкции одного ранга.
Конъюнктивная совершенная нормальная форма (КСНФ) представления булевой функции – это выражение булевой функции через макстермы одного ранга, связанные конъюнкцией. КСНФ еще называют каноническим произведением макстермов или стандартными произведением сумм.
Например, Р(x, y, z) = (x + y + z) · (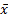 +
+ 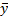 + z).
+ z).
Требования, предъявляемые к КСНФ:
- в ней недолжно быть двух одинаковых дизъюнкций;
- ни одна дизъюнкция не должна содержать двух одинаковых переменных;
- на одна дизъюнкция не должна содержать переменную вместе с ее отрицанием;
- все дизъюнкции одного ранга.
3.5. Построение булевой функции по таблице истинности обычно используется при анализе и синтезе логических схем микропроцессорных систем.
3.5.1 Построение булевой функции в форме канонической суммы минтермов осуществляют следующем образом:
- по каждому набору (строке) двоичных переменных, при котором функция принимает значение логической единицы, составляют минтермы (логические произведения);
-в полученные минтермы записывают прямое значение переменных, заданных логической единицей в таблице истинности, и инверсное – для тех переменных, которые в этой таблице заданы логическим нулём;
- соединяют минтермы операцией ИЛИ;
Пример 3.4. Построить булево выражение в форме канонической суммы минтермов по заданной таблице истинности:
| Х1 | Х2 | Х3 | ƒ |
Так как функция ƒ, заданная таблично, зависит от трех переменных и принимает значение логической единицы для трех наборов (строк 2, 3, 6) этих переменных, то булево выражение будет состоять из логической суммы трех минтермов третьего ранга, т.е.
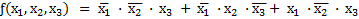 .
.
3.5.2. Построение булевой функции в форме канонического произведения макстермов осуществляют так:
- по каждому набору (строке) двоичных переменных, при котором функция принимает значение логического нуля, составляют макстермы (логические суммы);
- в полученные макстермы записывают инверсные значения переменных, заданных логической единицей в соответствующем
наборе, и прямое – для тех переменных, которые заданы логическим нулем;
- соединяют макстермы операции И.
Пример 3.5. Построить булево выражение в форму канонического произведения макстермов по заданной таблице истинности:
| х | у | z | F |
Заданная функция трех переменных F(x, y, z) принимает значение логического нуля при четырех наборах (строки 1, 2, 5, 7). Следовательно, булево выражение будет состоять из логического произведения четырех макстермов третьего ранга, т.е.
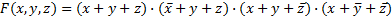 .
.
3.6. Законы булевой алгебры и соотношения, отражающие эти законы, приведены в табл. 2.4.
Коммуникативный, ассоциативный и дистрибутивный (для логического сложения) законы булевой алгебры полностью соответствуют аналогичным законам обычной алгебры.
Законы инверсии, отрицания, тавтологии и дистрибутивный закон для логического умножения являются специфичными законами для булевой алгебры.
С помощью законов и соотношений булевой алгебры производят эквивалентные преобразования с целью получения новых выражений, которые могут быть проще или сложнее исходных в зависимости от целей преобразования.
| Наименование | Условное обозначение | Соотношение | ||
| Для логического сложения | Для логического умножения | Для логического отрицания | ||
| Законы булевой алгебры | ||||
| Коммутативный(переместительный) | К | 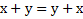
| 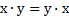
| - |
| Ассоциативный (сочетательный) | А | 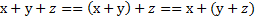
| 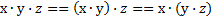
| - |
| Дистрибутивный (распределительный) | Д | 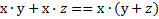
| 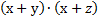
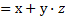
| - |
| Инверсии (двойственности или де Моргана) | И | 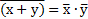
| 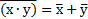
| - |
| Отрицания | О | 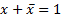
| 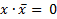
| 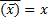
|
| Тавтологии (идемпотентности) | Т | 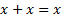
| 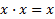
| - |
| Следствие законов булевой алгебры | С.1 | 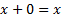
| 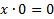
| - |
| С.2 | 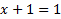
| 
| - | |
| С.3 | 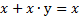
| 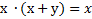
| - | |
| С.4 | 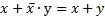
| 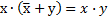
| - |
Пример 3.6. Упростить булево выражение
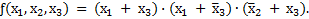
Это выражение можно упростить следующим образом:
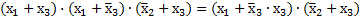
по закону Д;
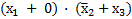 – по закону О;
– по закону О;
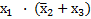 – по следствию С.1.
– по следствию С.1.
Пример 3.7. Упростить булево выражение
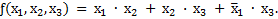
Это выражение упрощается следующим образом:
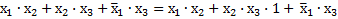
по следствию С2
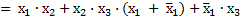
по закону О;
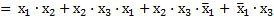 – по закону Д;
– по закону Д;
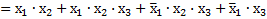 – по закону К;
– по закону К;
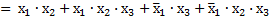 – по закону К;
– по закону К;
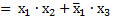 – по следствию С.3.
– по следствию С.3.
Пример 3.8. Выполнить отрицание выражения
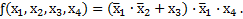
Отрицание заданного выражения выполняется последовательность:
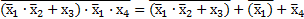
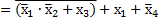
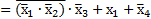
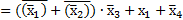
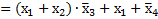
Таким образом, 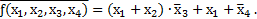
Пример 3.9. Построить каноническую сумму минтермов по выражению
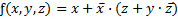 .
.
Построение канонической суммы минтермов производят следующим образом:
а) применив закон дистрибютивности (закон Д), представляют выражение в форме суммы произведений; в данном случае получим
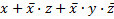 ;
;
б) модифицируют те члены, которые не являются минтерами, чтобы включить в них отсутствующие переменные. Так, первый член х, не содержащий y и z, домножается на 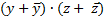 , что эквивалентно умножению на логическую единицу (согласно следствию, С.2), а второй член, не содержащий у, домножается на
, что эквивалентно умножению на логическую единицу (согласно следствию, С.2), а второй член, не содержащий у, домножается на 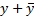 ; при этом с третьим членом, содержащим все переменные, ничего делать не нужно. Модифицированное выражение принимает вид
; при этом с третьим членом, содержащим все переменные, ничего делать не нужно. Модифицированное выражение принимает вид
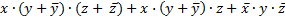 ;
;
в) применив закон дитрибютивности к модифицированному выражению и затем, если необходимо, закон тавтологии, получают каноническую сумму минтермов; для заданного выражения она имеет вид
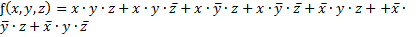
3.7. Минимизация булевых выражений – это преобразование булевых выражений с целью их упрощения, т.е. получение минимального числа минтермов или макстермов в булевом выражении и однородности выполняемых операций.
3.7.1. Метод непосредственных преобразований представляет собой преобразование и упрощение булевых выражений с использование законов и соотношений булевой алгебры.
Для его применения необходимо:
а) построить каноническую сумму минтермов, если функция задана таблицей истинности;
б) выявить соседние минтермы, т.е. такие, в которых имеется по одной несовпадающей переменной, например,
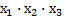 и
и 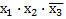 ;
; 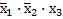 и
и 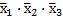 и т.п.;
и т.п.;
в) по отношению к соседним минтермам применить метод склеивания, базирующийся на законах дистрибутивности, отрицания и следствия С.2, в результате чего ранг минтермов понизится на единицу.
Например:
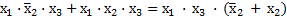 – по закону Д:
– по закону Д:
 – по закону О:
– по закону О:
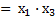 – по следствию С.2.
– по следствию С.2.
Минтермы, образованные в результате склеивания, называются импликантами. Полученные после первого склеивания импликанты при возможности склеивают повторно, и так до тех пор, пока склеивание возможно. Несклеиваемые импликанты называют простыми, а выражение, состоящие из простых импликант, называют тупиковым.
Если на некотором этапе склеивания образуется форма R, содержащая члены вида 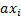 и
и 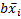 , то дальнейшее склеивание их осуществляют на базе закона дистрибутивности и следствия С.4.
, то дальнейшее склеивание их осуществляют на базе закона дистрибутивности и следствия С.4.
Например: 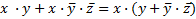 – по закону Д;
– по закону Д;
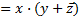 – по следствию С.4.
– по следствию С.4.
Пример 3.10. Используя метод непосредственных преобразований, минимизировать функцию трех переменных, заданную в форме канонической суммы минтермов:
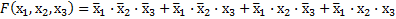 .
.
Выявляем соседние минтермы: первый и второй, третий и четвертый.
Применив метод склеивания по отношению к соседним минтермам, получим
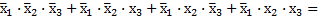
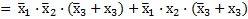 – по закону Д;
– по закону Д;
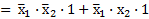 – по закону О;
– по закону О;
 – по следствию С.2.
– по следствию С.2.
К полученным импликантам применим повторное склеивание:
 – по закону Д;
– по закону Д;
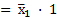 – по закону Д;
– по закону Д;
 – по следствию С.2.
– по следствию С.2.
Минимизированная функция имеет вид
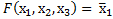
Пример 3.11. Используя метод непосредственных преобразований, минимизировать функцию трех переменных, заданную в следующем виде:
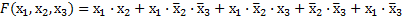
Так как функция задана не в форме канонической суммы минтермов, то выявляем формы R, содержащие члены 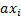 и
и 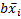 : это первая и вторая конъюнкции, содержащие
: это первая и вторая конъюнкции, содержащие 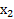 и
и 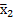 , для которых
, для которых 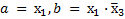 ; третья и четвертая конъюнкции, содержащие
; третья и четвертая конъюнкции, содержащие 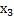 и
и 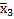 , для которых
, для которых 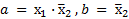 .
.
Применив метод склеивания к формулам R, получим
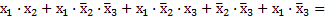
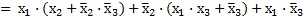
по закону Д.
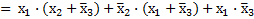 – по следствию С.4.
– по следствию С.4.
Воспользовавшись законом дистибутивности и затем опустив повторяющиеся члены (на основании закона тавтологии), получим каноническую сумму минтермов второго ранга:
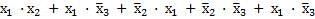 (повторяющийся член опускается).
(повторяющийся член опускается).
Выделяем соседние минтермы: первый, второй и третий.
Применив метод склеивания к соседним минтермам, получим
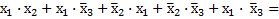
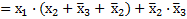 – по закону Д.
– по закону Д.
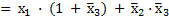 – по закону О;
– по закону О;
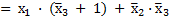 – по закону К;
– по закону К;
 – по следствию С.2.
– по следствию С.2.
Заменяя конъюнкцию отрицаний 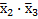 отрицанием дизъюнкций
отрицанием дизъюнкций 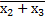 (на основании закона инверсии), получим минимизированное выражение
(на основании закона инверсии), получим минимизированное выражение
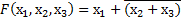 ,в котором выполняемые операции являются однородными.
,в котором выполняемые операции являются однородными.
3.7.2. Метод Карно – Вейча – это метод диаграмм Вейча, усовершенствованый Карно и применяемый при числе входных переменных не более 5 – 6.
Для миимизации булевых выражений используют карты Карно – графическое представление таблиц истинности т.е. своеобразный способ задания булевых выражений при помощи специальных таблиц, число клеток которых равно числу всех возможных наборов входных ппеременных, т.е. 2n (где n – число входных переменных), а запись в каждой клетке есть значение функции при соответствующих наборах входных переменных. Структура карт Карно для двух, трех и четырех входных переенных приведена на рис. 3.1 – 3.3 соответственно.
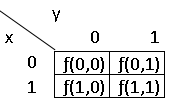
Рис. 3.1 Карты Карно для двух входных переменных

Рис. 3.2 Карты Карно для трех входных переменных

Рис. 3.3. Карты Карно для четырех входных переменных
Пример 3.12. Составить Карту Карно для булевой функции
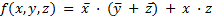 .
.
Составляем таблицу истинности, вычисляя значения выражения ƒ(x, y, z) для всех восьми комбинаций входных переменных по методике, изложенной в п. 2.3:
| x | y | z | F |
Строим карту Карно в соответствии с формой, показанной на рис. 3.2:
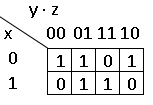
Минимизацию булевых функций, заданных в форме канонической суммы минтермов, с использованием карт Карно осуществляют следующим образом:
а) используя структуры карт Карно, записывают логическую единицу в клетке, соответствующие имеющимся в функции конъюнкциям. При этом свободные клетки заполняют логическими нулями;
б) «склеивают» в группы рядом расположенные логические единицы; любую логическую 1 можно склеивать сколько угодно раз. При выборе групп необходимо соблюдать следующие два принципа:
- группа должна быть как можно больше, так как при этом меньше число переменных и их инверсий в соответствующей конъюнкции; число ячеек в группе должно быть 2n, где n = 0, ∞;
- число групп должно быть как можно меньше, так как каждой группе соответствует конъюнкция;
в) в каждой группе отбирают те переменные на координатных осях, чьи значения не изменяются в пределах группы. Эти переменные и включают в соответствующие конъюнкции. Если переменные равны логическому нулю, то они входят в конъюнкции с отрицанием, а если равны логической единице – то без отрицания;
г) записывают окончательное выражение булевой функции как логическую сумму полученных конъюнкций.
Пример 3.13. Используя карты Карно, найти минимальную сумму функции двух переменных
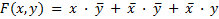 .
.
1. Строим карту Карно для двух переменных в соответствии с формой рис. 2.1, для чего в клетки, соответствующие конъюнкциям 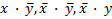 , записываем логическую единицу. Свободные клетки заполняем логическими нулями.
, записываем логическую единицу. Свободные клетки заполняем логическими нулями.
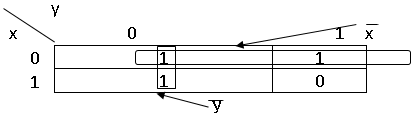
2. «Склеиваем» в группы логические единицы, находящиеся в двух соседних клетках строки или столбца (на карте полученные группы обведены сплошной линией).
3. Отбираем для каждой группы переменные, которые не изменяются в пределах группы:
- для первой группы (первого левого столбца) это 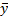 , поскольку переменная у в этой группе равна логическому нулю, а переменная х не сохраняет своего значения для этой группы;
, поскольку переменная у в этой группе равна логическому нулю, а переменная х не сохраняет своего значения для этой группы;
- для второй группы (верхняя строка) это 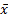 , так как переменная х в этой группе равна логическому нулю, а переменная у изменяется в пределах группы.
, так как переменная х в этой группе равна логическому нулю, а переменная у изменяется в пределах группы.
4. Записываем выражение булевой функции как сумму конъюнкций, содержащих только те переменные, которые не изменяются в склеиваемых клетках:
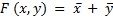 .
.
5. Преобразовываем полученное выражение в минимальную форму (на основании закона инверсии):
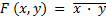
Пример 3.14. Используя карты Карно, найти минимальную сумму функции трех переменных
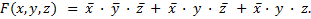
1. Строим карту Карно для трех переменных в соответствии с формой рис. 2.2, для чего в клетки, соответствующие конъюнкциям 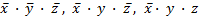 , записываем логическую единицу. Свободные клетки заполняем логическими нулями.
, записываем логическую единицу. Свободные клетки заполняем логическими нулями.
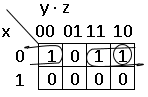
2. «Склеиваем» в группы логические единицы. Для карт Карно с тремя переменными карту следует рассматривать как цилиндр со склеенными правым и левым краями. Поскольку группы формируются на таком цилиндре, то на плоскости та или иная группа может оказаться разорванной. Поэтому рядом расположенными считаются логические единицы, находящиеся на ее левом и правом краях.
Соответствующая разорванной группе конъюнкция, полученная по описанным выше правилам, равна 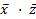 . Конъюнкция, соответствующая другой группе и полученная аналогично, равна
. Конъюнкция, соответствующая другой группе и полученная аналогично, равна 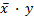 .
.
Булево выражение, представляющее собой сумму полученных конъюнкций, имеет вид
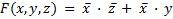
Преобразовав найденное выражение (на основании закона дистрибутивности), получим минимальную сумму заданной функции:
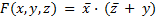
Пример 3.15. Используя карты Карно, найти минимальную сумму функции четырех переменных
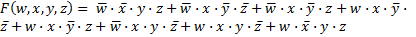
1. Строим карту Карно для четырех переменных в соответствии с формой рис. 2.3, для чего аналогично рассмотренным примерам записываем в клетки логические единицы и логические нули:
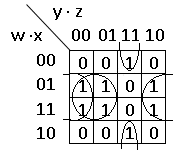
2. «Склеиваем» в группы логические единицы. Для карт Карно с четырьмя переменными карту следует рассматривать как поверхность тора. На таких картах рядом расположенными считаются логические единицы, находящиеся не только на левом и правом краях, но и на верхнем и нижнем краях.
Разорванной группе из четырех ячеек соответствует полученная по описанным выше правилам конъюнкция 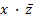 , а разорванной группе из двух ячеек -
, а разорванной группе из двух ячеек - 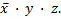
Квадратной группе, расположенной во второй и третьей строках, соответствует конъюнкция вида 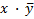 , переменные х и у которой не изменяются в пределах группы.
, переменные х и у которой не изменяются в пределах группы.
Записываем выражение булевой функции как сумму полученных конъюнкций:
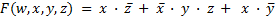 .
.
Преобразовываем найденное выражение в минимальную форму (на основании законов коммутативности, дистрибутивности и инверсии):
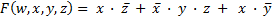
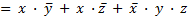 – по закону К;
– по закону К;
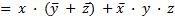 – по закону Д;
– по закону Д;
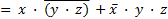 – по закону И.
– по закону И.
Пример 3.16. Используя карты Карно, найти минимальную сумму функции четырех переменных
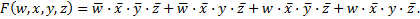
Особенностью данной функции является то, что соответствующие составляющим ее конъюнкциям логические единицы в карты Карно записываются в четырех углах:
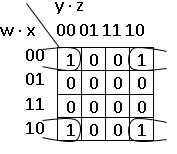
На таких картах логические единицы, находящиеся в четырех углах, считаются рядом расположенными и образуют одну группу, которой соответствует конъюнкция 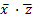 .
.
Таким образом, минимальная сумма заданной функции составит 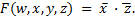
3.7.3 Частичные (на полностью определенные) булевы функции – это функции, определенные не для всех комбинаций входных переменных.
Для получения минимальной суммы частичной булевой функции необходимо доопределить – выбрать значения функции на запрещенных (недоопределенных) условиях. Это удобно сделать с помощью карт Карно, где недоопределенные условия обозначают прочерком в соответствующей ячейке. Такие ячейки могут быть произвольным образом включены в группы при построении минимальных сумм или же вообще не включены.
Пример 3.17. Построить минимальную сумму частичной булевой функции, представленной картой Карно:
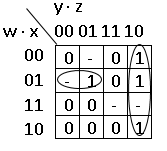
Применяя ранее описанное правило, находим конъюнкции для первой группы (вторая строка): 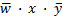 , и для второй (крайний правый столбец):
, и для второй (крайний правый столбец): 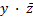 .
.
Минимальная сумма, порождаемая картой Карно, равна
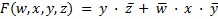
Варианты индивидуальных заданий
1. Определить значение истинности высказываний, заданных в табл. 3.5
Таблица 3.5
| Вариант | Высказывания | ||
| АЛУ микропроцессора выполняет операцию сложения или декодирования команд | |||
| Работу микропроцессора можно изменить увеличением размера памяти | |||
| 8 бит составляют два байта | |||
| Управляющие сигналы, генерируемые микропроцессором, предназначены для управления схемами памяти, ввода, вывода | |||
| Для функционирования микропроцессора необходимо устройство вывода | |||
| Команды микро – ЭВМ хранятся в памяти или в устройстве ввода | |||
| Цифра 2 в десятичном счислении 2364 является младшей значащей цифрой | |||
| Число 10120101 является двоичным | |||
| Восьмиразрядным двоичным числом можно представить 256 различных десятичных чисел | |||
| Счетчик команд микропроцессора не является регистром специального назначения | |||
| Число разрядов регистра команд определяется архитектурой микропроцессора | |||
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2019-01-11 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |