Отчет к лабораторной работе должен содержать:
• Титульный лист
• Название лабораторной работы
• Вариант
• Краткое описание последовательности выполнения задания.
• Поэтапное решение заданий варианта
• Вывод
Разрешается в отчетах делать описание менее детальными, чем это сделано в примерах.
Вопросы для самопроверки
1. Что такое система счисления?
2. В чем отличие позиционных систем счисления от непозиционных? Приведите примеры таких систем счисления.
3. Что называется основанием позиционной системы счисления?
4. Каковы общие правила перевода чисел в десятичную систему счисления?
5. Каковы общие правила перевода десятичных чисел в другие системы счисления?
6. Каковы правила перевода чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную?
7. Как выполняются арифметические действия в двоичной системе счисления?
8. Преобразуйте числа 183,5₁₀ по схеме (10)-(2)-(8)-10.
Лабораторная работа №2
Кодирование чисел
Цель работы: освоить методы представления чисел со знаком и в коде 8421; получить практические навыки по выполнению сложения и вычитания двоичных и десятичных чисел в прямом, обратном и дополнительном кодах и в коде 8421.
2.1. Кодирование двоичных чисел – это представление двоичных чисел со знаком.
Применяются следующие коды чисел: прямой, обратный, дополнительный. Знак «+» кодируется нулем «0», «-» - единицей (1), которые записывают в дополнительном старшем (знаковом) разряде.
Прямой код двоичного числа получают записью в знаковый разряд нуля для положительных и единиц отрицательных чисел.
Пример 2.1. Представить дробные двоичные числа х₁=₊0,1011₂ и х₂= -0,01011001₂ в прямом коде.
[х₁]пр = 0,1011; [х₂]пр = 1,01011001.
Пример 2.2. Представить целые двоичные числа В₁ = + 11010 и В₂ = -101101 в прямом коде.
[В₁]пр = 0.11010 и [В₂]пр = 1.101101.
В рассмотренных примерах запятая и точка отделяют знаковые разряды.
Обратный код положительного двоичного числа получается так же, как в прямом коде, т.е.
[ х ]обр = х пр, [ В ]обр = В пр.
Обратный код отрицательного двоичного числа образуется записью в старшем (знаковом) разряде единицы и заменой в разрядах двоичного числа нулей на единицы, а единицы на нули.
Пример 2.3. Представить дробные двоичные числа х ₁ = +0,1001₂ и
х₂ = -0,01101 ₂ в обратном коде.
Пример 2.4. Представить целые двоичные числа В₁ = +111001₂
и В₂ = - 110011011₂ в обратном коде.
[В₁]обр = 0.111001 и [В₂]обр = 1.001100100.
Дополнительный код отрицательного двоичного числа получается из обратного кода этого числа прибавлением единицы к младшему разряду.
Пример 2.5. Представить дробные двоичные числа х₁ = +0,1001₂
и х₂ = -0,01101₂ в дополнительном коде.
Пример 2.6. Представить целые двоичные числа В₁ = +111001₂
и В₂ = - 110011011₂ в обратном коде.
Представление ±0 в прямом, обратном и дополнительном кодах приведено в табл. 2.1.
Таблица 2.1.
| Значение | Прямой код | Обратный код | Дополнительный код |
| + 0 | 0.00 … 0 | 0.00 … 0 | 0.00 … 0 |
| - 0 | 1.00 … 0 | 1.11 … 1 | 0.00 … 0 |
Неоднозначность представление нуля в обратном коде (см. табл. 2.1) является одним из недостатков последнего.
2.2. Сложение и вычитание кодированных чисел производят при одинаковом их представлении, для чего числа со знаком перед кодированием выравнивают по числу разрядов добавлением нулей справа (для дробной части) и слева (для целой части) от исходных чисел.
Сложение двоичных чисел в прямом коде, когда у слагаемых одинаковые знаки, осуществляют суммированием их модулей по правилам двоичного сложения и присвоением сумме знака слагаемых.
Пример 2.7. Выполнить сложение в прямом коде следующих двоичных чисел:
х₁ = +0,001₂ и х₂ = +0,110₂; у₁ = -0,0100₂ и у₂ -= -0,1001₂;
А₁ = +1110₂ и А₂ = +1111₂; В₁ = -1000₂ и В₂ = -1011₂.
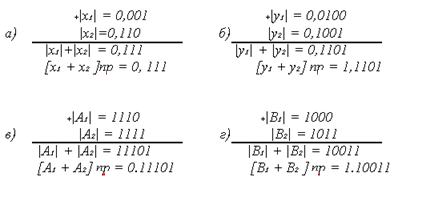
В связи с громоздкостью реализации операции вычитания в прямом коде ее в вычислительных устройствах не применяют, заменяя операцией сложения с использованием обратного или дополнительного кодов.
Сложение двоичных чисел в дополнительном коде осуществляют суммированием их кодов по правилам двоичного сложения, разряд за разрядом, включая старшие знаковые разряды кодов. При этом перенос из знакового разряда отбрасывают, а результат получают в дополнительном коде.
Примет 2.8. Выполнить сложение в дополнительном коде следующих двоичных чисел:
х₁ = +0,0011₂ и у₁ = +0,0101₂; х₂ = +0,0101₂ и у₂ = -0,0011₂;
х₃ = +0,0011₂ и у₃ = -0,0101₂; х₄ = -0,0011₂ и у₄ = -0,0101₂;
А₁ = +011₂ и В₁ = -110₂; А₂ = +110₂ и В₂ = -011₂;
А₃ = -011₂ и В₃ = -100₂.
Сложение двоичных чисел в обратном коде осуществляют суммированием кодов слагаемых по правилам двоичного сложения, включая знаковые разряды. При этом перенос из знакового разряда прибавляют к младшему разряду суммы (так называемый циклический перенос), а результат получают в обратном коде.
Пример 2.9. Выполнить сложение в обратном коде следующих двоичных чисел:
х₁ = +0,01011₂ и у₁ = -0,10101₂;
х₂ = +0,10111₂ и у₂ = -0,01010₂;
А₁ = +1001₂ и В₁ = -1110₂; А₂ = -0110₂ и В₂ = -1000₂;
Обращение положительного числа М, имеющего (n-1) – разрядное представление, - это результат вычисления по формуле
, (2.1)
где q - основание системы счисления.
(n-1) – разрядное представление числа возникает при кодировании отрицательных чисел, когда старший (знаковый) разряд содержит единицу.
Относительно обратного кода числа со знаком обращением называют операцию, состоящую в применении выражения (2.1) к величинной части кода и в замене значения знакового разряда на противоположное. Для обращения двоичных чисел, представленных в обратном коде, необходимо заменить каждый 0 на 1, а каждую 1 на 0, включая знаковый разряд.
Пример 2.10. Получить обращение чисел, представленных в двоичном обратном коде:
[ х ]обр = 0,01011; [ у ]обр = 1,01101;
[ А ]обр = 0.00101; [ В ]обр = 1.11001.
| Обозначение | Код | Обращение |
| х | 0,01011 | 1,10100 |
| у | 1,01101 | 0,10010 |
| А | 0.00101 | 1.11010 |
| В | 1.11001 | 0.00110 |
Дополнение положительного числа М, имеющего (n-1)- разрядное представление, - это результат вычисления по формуле
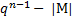. (2.2)
Относительно дополнительного кода взятием дополнения называют операцию, состоящую в применении вычисления (2.2) к величинной части кода и инвертировании значения знакового разряда. Для получения дополнения двоичных чисел, представленных в дополнительном коде, необходимо сначала выполнить обращение путем замены 0 и 1 в коде соответственно на 1 и 0. А затем прибавить к младшему разряду результата единицу.
Пример 2.117. Получить дополнение чисел, представленных в двоичном дополнительном коде:
[x]доп = 0,10110; [у]доп = 1,10001;
[А]доп = 0.10100; [В]доп = 1.11100.
| Обозначение | Код | Обращение | Дополнение |
| х | 0,10110 | 1,01001 | 1,01010 |
| у | 1,10001 | 0,01110 | 0,01111 |
| А | 0.10100 | 1.01011 | 1.01100 |
| В | 1.11100 | 0.00011 | 0.00100 |
Для вычитания двоичных чисел, представленных в дополнительном коде, необходимо сначала взять дополнение вычитаемого, а затем сложить его с кодом уменьшаемого.
Пример 2.12. Выполнить вычитание для следующих чисел, представленных в двоичном дополнительном коде:
0.1100 – 0.0111; 1,10100 – 0,00110
Для вычитания двоичных чисел, представленных в обратном коде, необходимо сначала получить обращение вычитаемого, а затем сложить его с кодом уменьшаемого.
Пример 2.13. Выполнить вычитание для следующих чисел, представленных в двоичном обратном коде:
1.1001 – 1.0010; 0,01001 – 1,01100
2.3. Двоично-кодированная десятичная схема – это схема кодирования, при которой каждую десятичную цифру представляют двоично-кодированной группой.
Схема 8421 ВДС – это двоично-кодированная десятичная схема, в которой десятичные цифры кодируют первыми десятью четырехразрядными двоичными числами, приведенными в табл. 2.2
Таблица 2.2
Двоичные коды десятичных цифр
| Десятичная цифра | Код 8421 | Десятичная цифра | Код 8421 |
Многоразрядные десятичные числа в коде 8421 представляют путем объединения групп, кодирующих отдельные десятичные цифры.
Пример 2.14. Представить в коде 8421 число 658₁₀.
658₁₀ = 0110 0101 1000
6 5 8
Сложение десятичных цифр в коде 8421производят в такой последовательности:
- суммируют числа по правилам двоичной арифметике;
- добавляют корректирующие слагаемое 6₁₀ = 0110₂ к каждой группе, в которой получена недопустимая комбинация (1010, 1011, 1100,1101., 1110, 1111) или возник перенос в следующую группу в процессе сложения.
Пример 2.15. Выполнить сложение чисел в коде 8421. Указать необходимые коррекции:
Вычитание десятичных чисел в коде 8421 производят по правилам двоичной арифметики с последующим вычитанием корректирующего числа 6₁₀ = 0110₂ из этой группы полученного результата, которая получила заем.
2.4 Кодирование десятичных чисел – это представление десятичных чисел со знаком. В качестве указателя знака, как и в двоичной системе счисления, используют двоичные цифры 0 и 1, которые записывают в старшем знаковом разряде. При этом нулем (0) кодируют знак «+», а единицей (1) – знак «-».
Прямой код десятичного числа получают добавлением знакового разряда к абсолютной величине.
Обратный и дополнительный коды положительного десятичного числа совпадают с его прямым кодом.
Пример 2.17. Представить десятичные числа
х₁ = +0,485₁₀; х₂ = +0,162₁₀; В₁ = +794₁₀; В₂ = +53₁₀
в прямом, обратном и дополнительном кодах.
[ х₁ ]пр = 0,485; [ х₁ ]обр = [ х₁ ]доп = 0,485;
[ х₂ ]пр = 0,162; [ х₂ ]обр = [ х₂ ]доп = 0,162;
[ В₁ ]пр = 0.794; [ В₁ ]обр = [ В₁ ]доп = 0.794;
[ В₂ ]пр = 0.53; [ В₂ ]обр = [ В₂ ]доп = 0.53.
Обратный код отрицательного десятичного числа образуется записью в знаковом разряде единицы, в следующих (n-1) – разрядах – десятичных цифр, соответствующих числу, которое получено вычитанием каждой цифры из 9.
Дополнительный код отрицательного десятичного числа получается из обратного кода этого числа прибавлением единицы к младшему разряду.
Пример 2.18. Представить десятичные числа в обратном и дополнительном кодах:
х = -0,1321; В = -57.
[ х ]обр = 1,8678; [ х ]доп = 1,8679;
[ В ]обр = 1.42; [ В ]доп = 1.43.
Обращение и дополнение положительных чисел, имеющих (n-1) – разрядное десятичное представление, определяют по формулам (1.2) и (1.3) соответственно при q = 10.
Относительно кодов, представляющих числа со знаком, обращением или взятием дополнения называют применение выражений (1.2) или (1.3) соответственно к величинной части кода и изменение значения знакового разряда на противоположное. Для обращения десятичных чисел, представленных в обратном коде, необходимо произвести вычитание каждой цифры из 9 и изменить значение знакового разряда на противоположное.
Для получения дополнения десятичных чисел, представленных в дополнительном коде, необходимо сначала выполнить обращение, а затем добавить единицу к результату обращения.
Пример 2.19. Получить обращение чисел, представленных в десятичном обратном коде:
[х]обр = 1,8678; [В]обр = 1.42;
[[хобр]]обр = 0,1321; [[Вобр]]обр = 0.57;
Пример 2.20. Получить дополнение чисел, представленный в десятичном дополнительном коде.
[х]доп = 1,8679; [В]доп = 1.43;
[[хдоп]]доп = 0,1321; [[Вдоп]]доп = 0.57;
Обращение кода или переход к дополнению кода эквивалентен замене знака, представляемого кодом числа, на противоположный.
При сложение десятичный чисел, представленных в обратном коде, суммируются величинные части кодов по правилам десятичной арифметики, а знаковые разряд складывают по правилам двоичной арифметики. При этом перенос из знакового разряда прибавляют к младшему разряду суммы (так называемый циклический перенос), а результат получают в обратном коде.
Пример 2.21. Выполнить десятичное сложение чисел, представленный в обратном коде:
0.76 + 1.65; 0.27 + 1.15
При вычитании десятичных чисел, представленных в обратном коде, сначала обращают вычитаемое, а затем осуществляют его сложение с кодом уменьшаемого.
Пример 2.22. Выполнить десятичное вычитание чисел, представленных в обратном коде:
0.37 – 0.12; 1.43 – 1.95
Сложение десятичных чисел, представленных в дополнительном коде, осуществляют аналогично десятичному сложению в обратном коде. Различие заключается в том, что в дополнительном коде перенос из знакового разряда игнорируются.
Пример 2.23. Выполнить десятичное сложение чисел, представленных в дополнительном коде:
0.35 + 1.26; 1.77 + 1.54.
При вычитание десятичных чисел, представленных в дополнительном коде, сначала необходимо взять дополнение вычитаемого, а затем сложить это дополнение с кодом уменьшаемого.
Пример 2.24. Выполнить десятичное вычитание чисел, представленных в дополнительном коде:
0.37 – 0.12; 1.44 – 1.92
Варианты индивидуальных заданий
1. Двоичные числа, заданные в прямом коде (табл. 2.3), преобразовать:
- к двоичному обратному коду и выполнить указанные действия;
- к двоичному дополнительному коду и выполнить указанные действия;
Таблица 2.3
| Вариант | Двоичные числа в прямом коде | Арифметические операции | ||
| a | b | Сложение,[a+b] | Вычитание,[a-b] | |
| 0,10010 | 0,00111 | + | + | |
| 0,0110 | 1,10100 | + | + | |
| 0,10110 | 1,11100 | + | + | |
| 1,01101 | 1,11001 | + | + | |
| 0,10010 | 0,00111 | + | + | |
| 1,10100 | 0,00110 | + | + | |
| 0,10110 | 1,11101 | + | + | |
| 1,01101 | 1,11001 | + | + | |
| 0,00110 | 0,01011 | + | + | |
| 0,10001 | 1,00101 | + | + | |
| 0,11001 | 1,01100 | + | + | |
| 1,10111 | 1,0110 | + | + | |
| 0,00110 | 0,01011 | + | + | |
| 1,01101 | 0,00110 | + | + | |
| 0,01001 | 1,01100 | + | + | |
| 1,10110 | 1,01101 | + | + | |
| 0,00101 | 1,00101 | + | + | |
| 1,10001 | 0,01000 | + | + | |
| 1,00111 | 1,01010 | + | + | |
| 0,01010 | 1,00111 | + | + | |
| 0,10100 | 0,10101 | + | + | |
| 0,11011 | 0,00100 | + | + | |
| 0,10010 | 0,00101 | + | + | |
| 1,01001 | 1,10011 | + | + |
2. Десятичные числа со знаком (табл. 2.4) представить.
- в десятичном обратном коде и выполнить указанные действия;
- в десятичном дополнительном коде и выполнить указанные действия;
Таблица 2.4
| Варианты | Десятичные числа | Арифметические операции | ||
| a | b | Сложение,[a+b] | Вычитание,[a-b] | |
| +632 | +87 | + | + | |
| -140 | +263 | + | + | |
| +417 | -343 | + | + | |
| -217 | -65 | + | + | |
| +326 | +67 | + | + | |
| -956 | +31 | + | + | |
| +408 | -372 | + | + | |
| -835 | -124 | + | + | |
| +450 | +237 | + | + | |
| -732 | +13 | + | + | |
| +620 | -63 | + | + | |
| -321 | -71 | + | + | |
| +806 | +46 | + | + | |
| -137 | +51 | + | + | |
| +895 | -23 | + | + | |
| -159 | -181 | + | + | |
| +322 | +22 | + | + | |
| -379 | +138 | + | + | |
| +426 | +56 | + | + | |
| -548 | +386 | + | + | |
| +214 | -172 | + | + | |
| -129 | -686 | + | + | |
| +586 | -17 | + | + | |
| -170 | -29 | + | + |
3. Десятичные числа (табл. 2.5) представить в коде 8421, выполнить указанные действия и указать необходимые коррекции:
Таблица 2.5
| Варианты | Десятичные числа | Арифметические операции | ||
| a | b | Сложение,[a+b] | Вычитание,[a-b] | |
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + | |||
| + | + |