Статистическая обработка данных по методу Стьюдента
К методам обработки количественных данных относятся статистическая обработка данных по методу Стьюдента. При этом вычисляются:
- среднее арифметическое, выражающее центральную тенденцию;
- среднеквадратическое отклонение, показывающее размах и особенности варьирования экспериментальных результатов;
- достоверность полученных материалов (по методу Стьюдента).
Рассмотрим, каким образом проводится статистическая обработка:
1. Находится среднее арифметическое, выражающее центральную тенденцию (М):

где: х - каждая величина изучаемой выборки,
S - знак сумма,
n - число членов выборки;
2. Находится среднеквадратическое отклонение, показывающее размах и особенности варьирования экспериментальных результатов (s):
 |
(2),
3. Сравнение выборок между собой с целью определения достоверности получаемых материалов проводился по методу Стьюдента.

|
.
где: t - коэффициент Стьюдента,
Х1 - каждый член из первой выборки,
Х2 - каждый член из второй выборки,
М1 - среднее арифметическое первой выборки,
М2- среднее арифметическое второй выборки,
n1 - количество членов первой выборки,
n2 - количество членов второй выборки.
n+n-2 - число степеней свободы.
Например, было проведено тестирование в двух группах детей. Полученные результаты в группах ЭГ и КГ представлены в таблице 15.1 и таблице 15.2.
| ЭГ Таблица 15.1 | КГ Таблица 15.2 | ||||
| № | Имя | Балл (%) | № | Имя | Балл (%) |
| Вася | Таня | ||||
| Толя | Галя | ||||
| Коля | Наташа | ||||
| Миша | Даша | ||||
| Костя | Юля | ||||
| Саша | Оля | ||||
| М1 | М2 |
Находим среднее арифметическое по формуле (1) и заносим его в графу 7 табл. 1 и 2.
М1=(51+50+53+49+53+48)/6=51;
М2=(49+51+48+49+51+50)/6=50.
Для вычисления среднеквадратического отклонения по формуле (2) для группы ЭГ (данные в таблице 15.1), построим следующую таблицу (таблица 15.3):
Таблица 15.3. – Вычисление среднеквадратического отклонения для группы ЭГ
| № | Х1 | Х1-М1 | (Х1-М1)2 |
| -1 | |||
| -2 | |||
| -3 | |||
| М1 |
В колонку Х1-М1 помещают разницу между значением параметра для каждого ребенка и средним арифметическим для выборки. В колонке (Х1-М1)2 полученную в предыдущей колонке величину возводят в квадрат.
Для нахождения числителя формулы (2), нужно сложить все числа в колонке (Х1-М1)2 (0+1+4+4+4+9)=22, извлечь из полученной суммы квадратный корень (=4,69). Знаменатель находится как квадратный корень из количества тестируемых, т.е. квадратный корень из 6 (=2,45).
Аналогичную таблицу строим для группы КГ:
Таблица 15.4. – Вычисление среднеквадратического отклонения для группы КГ
| № | Х2 | Х2-М2 | (Х2-М2)2 |
| -1 | |||
| -2 | |||
| -1 | |||
| М2 |
Сумма в колонке (Х2-М2)2 равна 8, следовательно среднеквадратическое 1,2.
Используя данные таблиц 15.3 и 15.4 легко сделать вычисления по формулам (3) для нахождения коэффициента Стьюдента.
 |
S2=1
 Теперь не сложно найти значение t=(51-50)/Ö S2 = 1
Теперь не сложно найти значение t=(51-50)/Ö S2 = 1
В справочной таблице (её можно взять в психологии Р. Немова – 3 том) следует сравнить полученное значение с табличным. Табличное значение находится исходя из степени свободы (n1+n2-2) и уровня значимости (для психологических исследований он равен 0,05). Если табличное значение больше полученного, то различия в группах не значимые. Так получилось и в нашем случае. Табличное значение для числа степеней свободы 10 и уровня значимости 0,05 равно 2,228 по сравнению с полученной нами 1. ОТЛИЧИЯ В ГРУППАХ ЭГ и ЭК не значимые.
Техника вычисления хи-квадрата (критерий Пирсона)
Другой метод статистической обработки данных – обработка данных по критерию Пирсона (хи-квадрат)
Рассмотрим пример со сдачей экзаменов в вуз выпускниками 1-ой и 2-ой школ. Всего намерены были сдавать экзамены 187 человек. Из их числа на долю 1-ой школы приходится 53,5 % (100 человек), а на долю 2-ой школы – 46,5 % (87 человек). Положим, что выпускники той и другой школы подготовлены одинаково, тогда и доли сдавших и несдавших будут такие же, как доли их представленности в числе сдающих. Всего сдало экзамены 126 выпускников. Согласно высказанному предположению, 53,5 % от этого числа должны бы были прийтись на 1-ую школу – это составит 66,9 от 126 - и 46,5 % на 2-ую школу ставит 58,9 от 126. Такое же рассуждение повторяем относительно не сдавших. Их всего 61 человек. На 1-ю школу, как нам известно, должно, по предположению должно прийтись 53,5% от этого числа, т. е. 33,0 от 61 долю 2-ой школы — 46,5%, т. е. 28,1 от 61. Однако в условиях этого исследования другое распределение. Количество выпускников 1-ой школы, сдавших экзамены, составляет 82, а не 66,9, как было рассчитано. Количество выпускников 2-й школы, сдавших экзамены составляет в действительности 44, а не 58,6. Сравнивая количество не сдавших (с предполагаемым распределением) по 1 школе – 18, а не 33, во 2-ой 43, а не 28,1.
Расхождение на налицо. Он и-то и учитываются при вычислении хи-квадрат. Отразим это в таблице 15.5. Количества, которые были бы получены при принятии нуль-гипотезы заключены в скобки. В правом углу буквенное обозначение клетки.
Получены разности по клеткам (знак разности не существенен):
А fА=82-66,9=15,1
В fВ=18-33=15
С fС=44-58,9=14,9
Д fД=43-28,1=14,9
Таблица 15.5. – Вычисление хи-квадрата
| Школы | Число сдавших | Число не сдавших | Всего | Долевые отношения |
| 82 А (66,9) | 18 В (33,0) | (100) | 53,5 % | |
| 44 С (58,9) | 43 Д (28,1) | (87) | 46,5 % | |
| Всего | 100 % |
Формула хи-квадрат:
 |
где: fo - наблюдаемые численности,
fe - предполагаемые (теоретические) численности.
Для определения значения c2 по таблице, необходимое число степеней свободы определяется по формуле (2):
f= (k-1) (c-1) (2),
где: k - число рассматриваемых категорий;
с - число сравниваемых групп.
f=(2-1)(2-1)=1
По таблице c20.05=3,84.
Если табличное значение больше полученного, то различия в группах не значимые.
Коэффициент ранговой корреляции Rs (Спирмена)
Метод ранговой корреляции Спирмена позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или Двумя профилями (иерархиями) признаков.
Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы (определен ранг). Такими рядами значений могут быть:
-два признака, измеренные в одной и той же группе испытуемых;
-две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (например, личностные профили по 16-факторному опроснику Р.Б. Кеттелла, иерархии ценностей по методике Р. Рокича, последовательности предпочтений в выборе из нескольких альтернатив и др.);
-две групповые иерархии признаков;
-индивидуальная и групповая иерархии признаков.
Вначале показатели ранжируются отдельно по каждому из признаков. Как правило, меньшему значению признака начисляется меньший ранг.
Для курсового проекта чаще встречается первый вариант. Рассмотрим его (напомним, участвуют два признака). Здесь ранжируются индивидуальные значения по первому признаку, полученные разными испытуемыми, а затем индивидуальные значения по второму признаку.
Если два признака связаны положительно, то испытуемые, имеющие низкие ранги по одному из них, будут иметь низкие ранги и по другому, а испытуемые, имеющие высокие ранги по одному из признаков, будут иметь по другому признаку также высокие ранги. Для подсчета Rs необходимо определить разности (d) между рангами, полученными данным испытуемым по обоим признакам. Затем эти показатели определенным образом преобразуются и вычитаются. Чем меньше разности между рангами, тем больше будет Rs, тем ближе он будет к +1.
Если корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия. Формула составлена так, что в этом случае Rs окажется близким к 0.
В случае отрицательной корреляции низким рангам испытуемых по одному признаку будут соответствовать высокие ранги по другому признаку и наоборот.
Чем больше несовпадение между рангами испытуемых по двумя переменным, тем ближе Rs к –1.
Значимость полученного коэффициента корреляции определяется по количеству ранжированных значений N. В первом случае это количество будет совпадать с объемом выборки n.
Если абсолютная величина Rs, достигает критического значения или превышает его, корреляция достоверна.
Ограничения коэффициента ранговой корреляции:
1. По каждой переменной должно быть представлено не менее 5 наблюдений.
2. Верхняя граница выборки определяется имеющимися таблицами критических значений (не более 40)
3. Коэффициент ранговой корреляции Спирмена Rs, при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения.
В этом случае, необходимо вносить поправку на одинаковые ранги.
Пример 1 - корреляция между двумя признаками. Признак А – количество ошибок авиадиспетчера. Признак Б – его интеллект (методика Д. Векслера)
Алгоритм расчета коэффициента ранговой корреляции Спирмена rs.
1.Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.
2. Проранжировать значения переменной А, начисляя ранг 1 наименьшему значению. Занести ранги в первый столбец таблицы по порядку номеров испытуемых или признаков
3.Проранжировать значения переменной В, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.
4.Подсчитать разности dмежду рангами А и В по каждой строке таблицы и занести в третий столбец таблицы.
5. Возвести каждую разность в квадрат: d 2. Эти значения занести в четвертый столбец таблицы.
6. Подсчитать сумму квадратов.
7. Посчитать поправки
Tа=∑(a3-a)/12
Tb=∑(b3-b)/12
Где а и в объем одинаковых рангов в ранговых рядах
8. Рассчитать коэффициент ранговой корреляции Rs, по формуле:
а) при отсутствии одинаковых рангов
rs=1-6
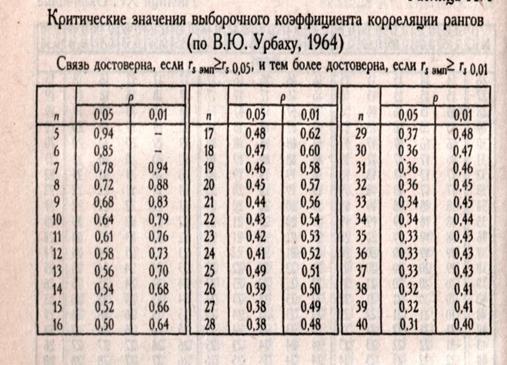
9. Определить по таблице критическое значение Rs для данного N.
Если Rs превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от 0.
б) при наличии одинаковых рангов:
Для определения значимости Rs, неважно, является ли он положительным или отрицательным, важна лишь его абсолютная величина
Заключение
Вы ознакомились с общими требованиями, предъявляемыми к курсовому проекту и рекомендациями по её подготовке и защите. Выполнение этих рекомендаций представляет необходимое, хотя и недостаточное условие успешной, методологически грамотной научной работы. Данные рекомендации остаются актуальными и при выполнении курсовых работ (проектов) и по другим дисциплинам.
Приложение 1