Точность оценки, доверительная вероятность (надежность)
Доверительный интервал
Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, – точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Пусть найденная по данным выборки статистическая характеристика 
служит оценкой неизвестного параметра 
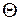. Ясно, что тем точнее определяет параметр 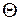, чем меньше абсолютная величина разности 
. Другими словами, если 
и 
, то чем меньше 
, тем оценка точнее. Таким образом, положительное число характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству . Можно лишь говорить о вероятности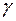 
, с которой это неравенство осуществляется.
Надежностью оценки 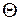по называют вероятность 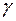, с которой осуществляется неравенство . Обычно надежность оценки задается наперед, причем в качестве 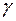берут число, близкое к единице. Наиболее часто задают надежность равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что , равна :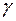
.
Заменив неравенство равносильным ему двойным неравенством 
, или 
, получим
.
Вероятность того, что интервал 
заключает в себе (покрывает) неизвестный параметр 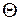, равна .
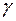Доверительным называют интервал , который покрывает неизвестный параметр с заданной надежностью .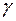
Доверительные интервалы для оценки
Математического ожидания нормального
распределения при известном s
Пусть количественный признак 
генеральной совокупности распределен нормально, причем среднее квадратическое отклонение 
этого распределения известно. Требуется оценить неизвестное математическое ожидание 
по выборочной средней 
. Найдем доверительные интервалы, покрывающие параметр с надежностью .
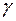Будем рассматривать выборочную среднюю как случайную величину 
( изменяется от выборки к выборке), а выборочные значения признака 
– как одинаково распределенные независимые случайные величины 
(эти числа также изменяются от выборки к выборке). Математическое ожидание каждой из этих величин равно 
и среднее квадратическое отклонение – .
Если случайная величина распределена нормально, то выборочная средняя , найденная по независимым наблюдениям, также распределена нормально (без доказательства). Параметры распределения таковы
, 
.
Потребуем, чтобы выполнялось соотношение
,
где 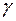– заданная надежность.
В формуле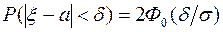 
заменим на и на , тогда получим
,
где 
.
Выразив 
, можем записать в виде
.
Учитывая, что вероятность 
задана и равна g, окончательно получим
.
С надежностью 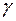можно утверждать, что доверительный интервал 
покрывает неизвестный параметр ; точность оценки .
Число 
определяется из равенства 
, по таблице функции Лапласа находят аргумент, которому соответствует значение функции Лапласа, равное 
.
Пример. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением 
. Найти доверительный интервал для оценки неизвестного математического ожидания по выборочной средней =5,4, если объем выборки 
и задана надежность оценки 
.
Найдем . 
или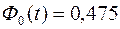 
. По таблице находим 
.
Найдем точность оценки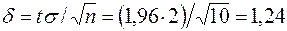 
.
Доверительный интервал (4,16; 6,64)