Геометрическая вероятность

Случайные события

Введение

Случайное событие – это любой исход опыта, который может произойти или не произойти.

Пример 1. Опыт: бросание игральной кости. События:

А – выпадение 4 очков,

В – выпадение нечетного числа очков,

С – выпадениене более 5 очков,

D – выпадение не более 6 очков,

Е – выпадение более 6 очков.

 

Элементарные события – это непосредственные исходы опыта. Множество всех элементарных событий называется пространством элементарных событий (ПЭС).

 

В примере 1 шесть элементарных событий:

ω₁ ω₂ ω₃ ω₄ ω₅ ω₆.

Событие ω₁ – выпадение 1 очка, ω₂ – выпадение 2 очков и т.д. Таким образом,

А = { ω₄ },

В= { ω₁, ω₃, ω₅ },

С= { ω₁, ω₂, ω₃, ω₄, ω₅ },

D= { ω₁, ω₂, ω₃, ω₄, ω₅, ω₆ },

E=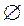

Событие называется невозможным, если оно заведомо не произойдет в результате опыта.

 

Невозможное событие обычно обозначают символом .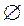

 

Событие называется достоверным, если оно обязательно произойдет в результате опыта.

 

Достоверное событие обычно обозначают символом Ω.

В примере 1 событие D – достоверное, а событие Е – невозможное.

 

Два события несовместны, если появление одного исключает появление другого события в одном опыте. В противном случае события называются совместными.

 

В примере 1 события А и В несовместны, а события А и С совместны.

 

Несколько событий образуют полную группу, если они несовместны и в результате опыта происходит только одно из них.

 

Опыт: бросание монеты. События:

А - выпадение орла,

В - выпадение решки.

События А и В образуют полную группу. События

ω₁ ω₂ … ω₆

в примере 1 также образуют полную группу.

Алгебра событий

Следуя академику Колмогорову А.Н., рассмотрим основные операции над событиями.

 

Суммой событий А и В называется событие

С=А+В,

состоящее в наступлении хотя бы одного из них.

Произведением событий А и В называется событие

С=АВ,

состоящее в совместном их наступлении.

Разностью событий А и В называется событие

С=А-В,

состоящее в наступлении события А, но ненастулении события В.

Противоположным событию А называется событие 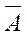, которое происходит тогда, когда не происходит событие А.

 

Другими словами, событие 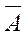означает, что событие А не наступило.

 

Событие А влечет событие В, т.е.

,

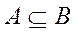если из наступления события А следует наступление события В.

 

Два события А и В равны, т.е.

А = В,

есл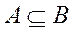и и .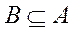

 

По данным примера 1 имеем

А+В= { ω₁, ω₃, ω₄, ω₅,},

АВ= ,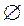

,

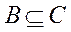В+С=С.

Действия над событиями обычно иллюстрируют с помощью диаграмм Эйлера-Венна.

Свойства операций над событиями:

1)

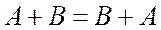
2)

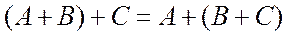
3)

4)

5)

6)

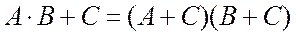
7)

8)

9)

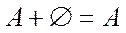
10)

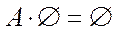
11)

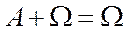
12)

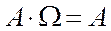
13)

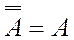
14)

15)

16)

17)

18)

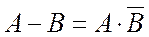
19)

20)

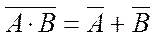
21)

Задача. Релейная схема состоит из 5 элементов. События А₁, А₂, …, А₅ состоят в том, что в течение некоторого времени соответствующий элемент работает, а событие А состоит в том, что вся схема в течение этого времени работает безотказно. Выразить событие А через события А₁, А₂, …, А₅

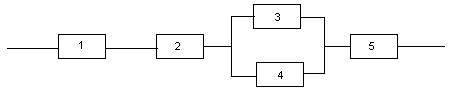
Рис.1

 

Пространство элементарных событий Ω может быть конечным, счетным или континуальным. В случае континуального пространства рассматривают так называемые σ-алгебры событий (по аналогии с σ- алгебрами множеств).

 

Класс S подмножеств пространства Ω называется

σ-алгеброй событий, если:

1) ,

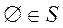2)

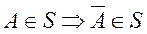
3)

 

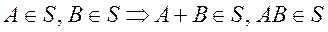
Операции сложения и умножения событий распространяются на случай счетного множества подмножеств, т.е. если

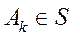
то

 

 

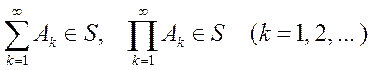
Определение вероятности

Пусть в n повторяющихся опытах событие А наступает m раз. Число m называют частотой этого события.

 

Относительной частотой или частостью события А называется величина

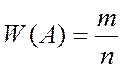(1)

 

Относительная частота обладает свойством статистической устойчивости, т.е. с увеличением числа опытов она принимает значения, близкие к некоторому определенному числу. Это число называют статистической вероятностьюсобытия А и обозначают P (A). Таким образом,

 

Статистическая вероятность – это предельный устойчивый уровень относительной частоты, т.е.

(2)

 

Ниже будет рассмотрена известная теорема Бернулли, являющая математическим обоснованием такой близости.

Классическое определение вероятности базируется на следующих рассуждениях. Пусть проводится опыт с n исходами. Предположим, что все исходы равновозможны и образуют полную группу.

Исход называется благоприятствующим, если он приводит к наступлению события.

 

Вероятностью события А называется отношение числа исходов, благоприятствующих этому событию к общему числу исходов, т.е.

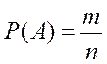(3)

 

Из определения вероятности вытекают следующие свойства:

1.

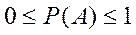
2.

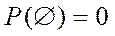
3.

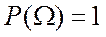
4. , если события А и В несовместны

Пример 2. В урне находятся 7 белых и 3 черных шара. Какова вероятность наудачу вытянуть

1) белый шар?

2) белый или черный шар?

3) красный шар?

Решение. Опыт: вынимание одного шара из урны.

1) Рассмотрим событие А – вынут белый шар. Число всевозможных исходов равно 10.Число случаев, благоприятствующих наступлению события А, равно 7.Значит, по формуле (3)

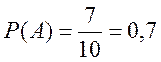
2) Рассмотрим событие В – вынут белый или черный шар. Очевидно, что это достоверное событие. Значит,

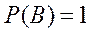
3) Рассмотрим событие С – вынут красный шар. Очевидно, это невозможное событие. Значит,

Пример 3. В урне находятся 7белых и 3 черных шара. Какова вероятность того, что из 5 вынутых шаров 3 окажутся белыми?

Решение. Пусть событие А - из 5 вынутых шаров 3 шара белые. Общее число исходов равно

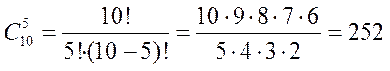
Число исходов, благоприятствующих наступлению события А, равно

Следовательно, по формуле классической вероятности

 

Пример 4. Имеется 6 карточек с буквами

Н М И Я Л О

Найти вероятность того, что получится слово МОЛНИЯ (событие А), если наугад одна за другой выбираются все шесть карточек.

Решение. Сначала найдем всевозможные исходы. Это перестановки из 6 элементов без повторений:

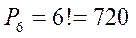
Благоприятный исход один, так как все буквы разные. Значит,

 

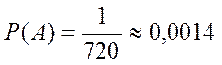
Пример 5. Имеется 6 карточек с буквами

А С Н Н А А

Найти вероятность того, что получится слово АНАНАС (событие В), если наугад одна за другой выбираются все шесть карточек.

Решение. Сначала найдем всевозможные исходы. Это перестановки из 6 элементов с повторениями. Заметим, что буква А повторяется 3 раза, а буква Н - 2 раза. Следовательно,

Таким образом,

 

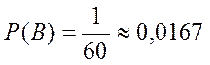
Геометрическая вероятность

 

Если ПЭС бесконечно, а исходы опыта равновозможны, то целесообразно применять геометрическое определение вероятности.

Рассмотрим некоторую область , а также внутри ее область 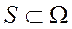. В области случайно выбирается точка 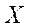. Будем говорить, что точка 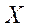брошена в область . Попадание точки в эту область будем считать достоверным событием, а попадание точки в область - случайным событием. Обозначим его .

Меру областей , будем обозначать, соответственно, 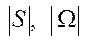. Мерой отрезка будем считать его длину, мерой фигуры – ее площадь, мерой тела – его объем

Геометрической вероятностью события называется отношение площади области к площади области :

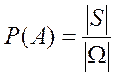(4)

 

Геометрическая вероятность обладает всеми свойствами классической вероятности.

 

Пример 6. На отрезок длины 10 см наудачу нанесена точка. Эта точка делит отрезок на два отрезка. Найти вероятность того, что меньший отрезок будет длиннее 2 см (событие G)

Решение. Событию G будет благоприятствовать ситуация, когда наудачу брошенная точка попадет на отрезок CD

Рис.2

Длина этого отрезка равна 6 см. таким образом,

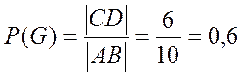
Пример 7. В круг радиуса 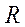вписан правильный треугольник. Найти вероятность того, что точка, брошенная в круг, попадет в треугольник.

Решение. Площадь круга равна 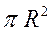. Найдем площадь правильного треугольника через радиус описанной окружности .

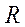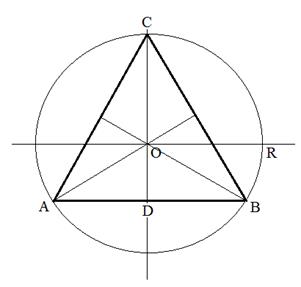
Рис.2

Из треугольника имеем:

Далее

Тогда площадь треугольник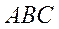а равна

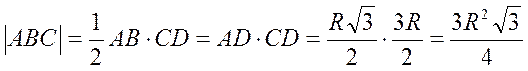
Итак,

 

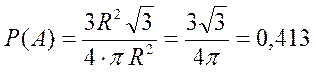
Пример 8. Стержень, длиной 12 см разломан на 3 части. Какова вероятность того, что из полученных частей можно составить треугольник (событие )?

Решение. Будем считать, что такой разлом равновероятен в любой точке стержня. Найдем сначала все возможные исходы.

Пусть длина первой части стержня равна 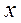, второй - 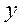. Тогда длина третьей части в соответствии с условием задачи составит 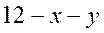. Все возможные исходы задаются системой:

или

Геометрически такая система задает множество точек треугольника 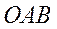, являющегося пересечением вертикальной полосы , горизонтальной полосы 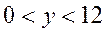и полуплоскости 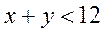, содержащей начало координат.

Рис.3

Найдем теперь исходы 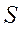, благоприятствующие наступлению события . Из элементарной геометрии известно, что в любом треугольнике сумма длин двух сторон должна быть больше длины третьей стороны, поэтому благоприятствующие исходы определяются системой:

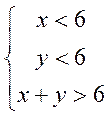
Геометрически такая система задает множество точек треугольника 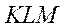, являющегося пересечением полуплоскости , содержащей начало координат, полуплоскости , также содержащей начало координат, и полуплоскости 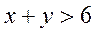, не содержащей начало координат

 

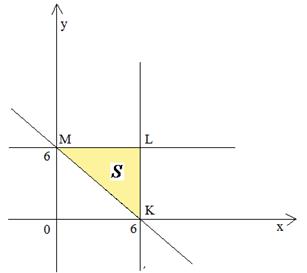
Рис.4

Налагая рисунок 4 на рисунок 3, получаем

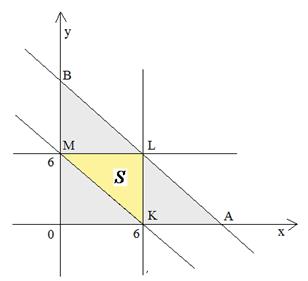
Рис.5

Нетрудно понять, что площадь треугольника 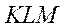в 4 раза меньше площади треугольника 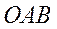. Таким образом,

 

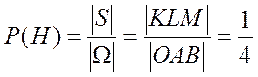
Условная вероятность

 

Рассмотрим два события и в некотором опыте. Наступление одного из этих события может влиять на вероятность наступления другого. Для характеристики зависимости одних событий от других вводится понятие условной вероятности

Условной вероятностью события при условии, что событие уже наступило, называется отношение вероятности произведения этих событий к вероятности события , причем 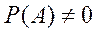и обозначается :

(5)

Аналогично определяется условная вероятность события при условии, что событие наступило:

(6)

Пример 9. В урне 3 белых и 7 черных шаров. Из нее один за другим вынимают 2 шара. Какова вероятность того, что второй шар окажется белым, если первый шар был черным?

Решение. Рассмотрим 2 события:

- первый вынутый шар черный,

- второй вынутый шар белый.

Решим задачу двумя способами.

1) Пусть событие произошло. Значит, в урне осталось 9 шаров, из них 3 белых. Тогда

2) По формуле (3) имеем

Найдем 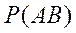. Общее число исходов, т.е. появление двух шаров, равно . Число исходов, благоприятствующих появлению события 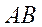, равно

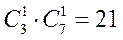
Значит,

Тогда по формуле (5)

 

 

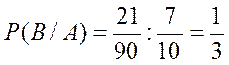
Независимые события

 

Из формул (5) и (6) следует, что

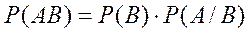(7)

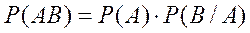(8)

 

Таким образом, вероятность произведения двух событий равна вероятности одного на условную вероятность другого. Формулы (7) и (8) называют также теоремами умножения зависимых событий.

Событие называется независимым от события , если его условная вероятность равна безусловной, т.е.

 

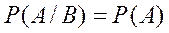
Если событие не зависит от события , то и событие не зависит от события . Действительно, из равенств (5) и (6) следует, что

т.е.

Это означает, что событие не зависит от события .

Для независимых событий теорема умножения принимает более простой вид.

 

Вероятность произведения двух независимых событий равна произведению их вероятностей

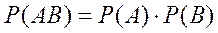(9)