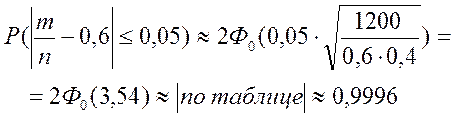Предельные теоремы схемы Бернулли

 

Если количество испытаний в схеме Бернулли велико, то подсчитать вероятность 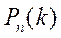практически невозможно. В этом случае пользуются приближенными, предельными или так называемыми асимптотическими формулами. Рассмотрим три предельные теоремы, содержащие асимптотические формулы для вычисления :

· Теорема Пуассона

· Локальная теорема Лапласа

· Интегральная теорема Лапласа

 

Теорема Пуассона. Если число испытаний неограниченно увеличивается, т.е 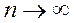, а вероятность 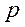наступления события в одном испытании неограниченно уменьшается, т.е. 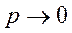, причем их произведение 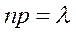практически постоянно, то вероятность удовлетворяет предельному равенству:

 

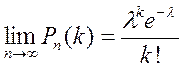
Из этого предельного равенства вытекает асимптотическая формула Пуассона:

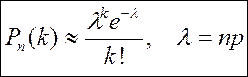(15)

Формула Пуассона (15) применяется в теории надежности, в теории массового обслуживания…

Пример 16. Предприятие по разливу прохладительных напитков отправило потребителю 1500 бутылок лимонада. Вероятность того, что в пути бутылка повредится, равна 0,002. Вычислить вероятность того, что при перевозке партии товара будет повреждено не более четырех бутылок (событие ).

Решение. В нашей задаче 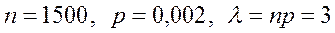. Вероятность события равна

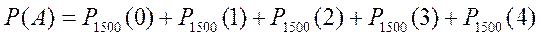
По формуле Пуассона (15) имеем

 

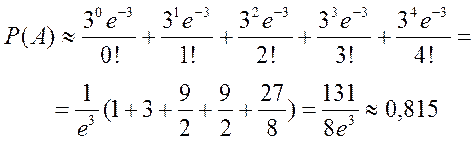
Локальная теорема Муавра-Лапласа. Если число испытаний велико, т.е 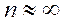, а вероятность 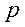наступления события в одном испытании постоянна, причем 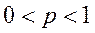, то вероятность 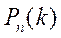удовлетворяет приближенному равенству:

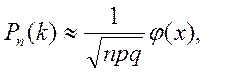(16)

где

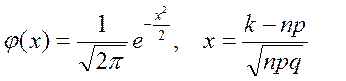(17)

Следует отметить, что приближенное равенство (16) тем точнее, чем больше число испытаний . Функцию (17) называют функцией Гаусса, а ее график, представленный на рисунке 7, – кривой вероятностей.

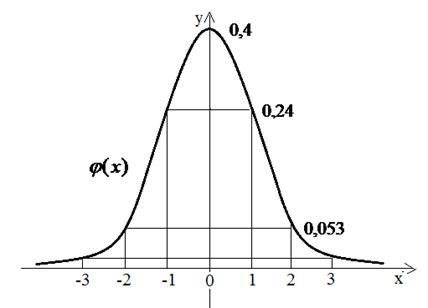
Рис.7

Для функции Гаусса составлены таблицы ее значений, находящиеся, как правило, в приложениях книг по теории вероятностей. Отметим некоторые свойства этой функции:

1) Функция 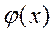бесконечно дифференцируема на всей числовой прямой

2) 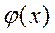четна, т.е.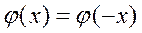

3) 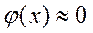при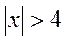

 

Пример 17. Вероятность попадания в мишень при одном выстреле равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.

Решение. По условию задачи

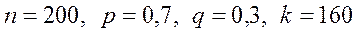
Тогда по формулам (17) имеем

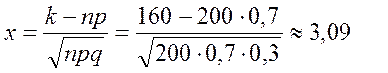
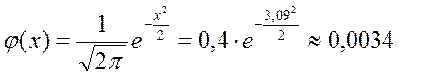
Далее по формуле (16) окончательно получаем

 

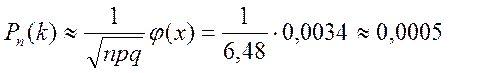
На практике более интересной является задача вычисления вероятности 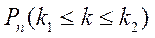того, что некоторое событие появится не менее 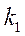раз и не более 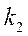раз. В этом случае используют интегральную теорему Лапласа

 

Нормированным интегралом Лапласа называется интеграл с переменным верхним пределом

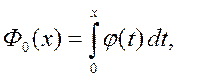
где 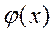- функция Гаусса (17).

 

Нормированный интеграл Лапласа является нечетной функцией, т.е. 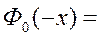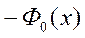, 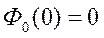. Кроме того,

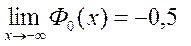
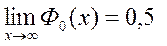
График этой функции представлен ниже.

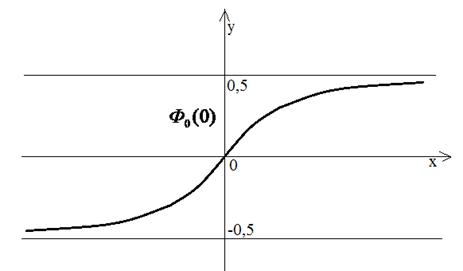
Рис.8

 

 

Интегральная теорема Муавра-Лапласа. Если число испытаний велико, т.е 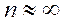, а вероятность 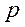наступления события в одном испытании постоянна, причем 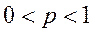, то вероятность 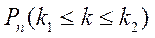удовлетворяет приближенному равенству:

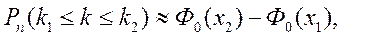(18)

где 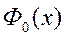- нормированный интеграл Лапласа,

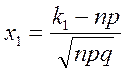
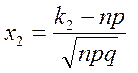(19)

 

Очевидно, что формула (18) эквивалентна формуле

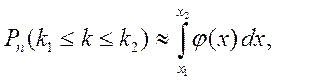(20)

В самом деле,

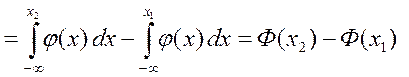
Наряду с нормированным интегралом Лапласа используют так называемую интегральную функцию распределения Лапласа или просто интеграл Лапласа

Интегралом Лапласа называется интеграл с переменным верхним пределом

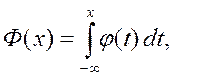
где 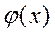- функция Гаусса (17).

 

Из свойств нормированного интеграла Лапласа вытекает, что

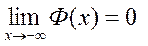
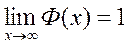
График этой функции представлен ниже.

 

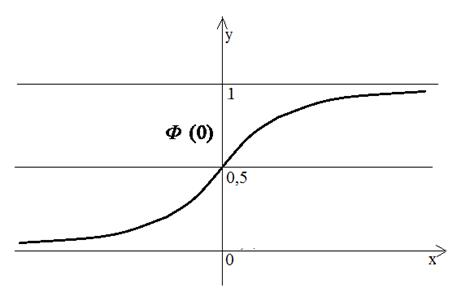
Рис.9

 

Ясно, что график интеграла Лапласа полностью совпадает с графиком нормированного интеграла Лапласа с точностью до сдвига вверх по оси 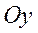на 0,5:

Значит, формулу (18) можно переписать так:

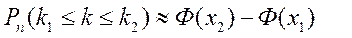(21)

Интеграл Лапласа является «неберущимся» интегралом, т.е. его нельзя выразить через конечное число элементарных функций. Для этого интеграла также составлены таблицы его значений, находящиеся, как правило, в приложениях книг по теории вероятностей.

 

Пример 18. Предприятие выпускает примерно 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого предприятия. Если среди них окажется более 10 изделий не высшего сорта, то вся партия бракуется и отправляется обратно на предприятие. Какова вероятность, что партия товара будет принята потребителем?

Решение. По условию задачи

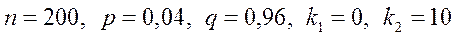
Тогда по формулам (19) имеем

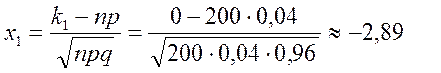
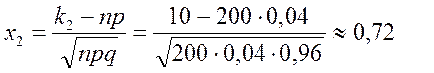
По таблице значений нормированного интеграла Лапласа находим

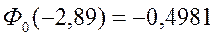
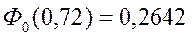
Далее по формуле (18) окончательно получаем

 

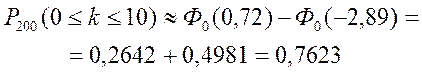
Интегральная формула Лапласа позволяет найти вероятность отклонения относительной частоты 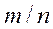от вероятности 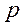в 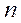независимых испытаниях. Напомним, что здесь 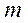- число исходов, благоприятствующих наступлению события, 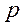- вероятность наступления этого события в одном испытании. Имеет место формула

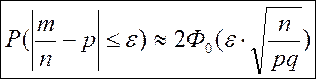(22)

где 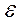-некоторая заданная точность.

Действительно, из неравенства

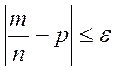
следует, что

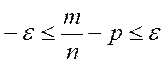
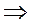
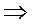
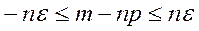
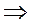
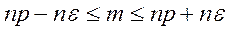
Тогда по формулам (18), (19) получаем

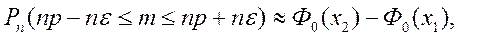
где

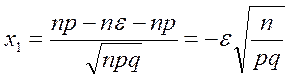
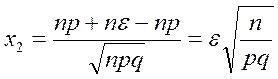
Далее

 

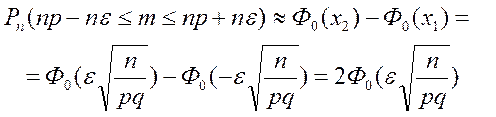
Пример 19. Найти вероятность того, что при 1200 выстрелах в цель отклонение частости 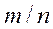от вероятности попадания в цель при одном выстреле 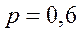не превышает по модулю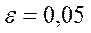

Решение. По формуле (22) получаем